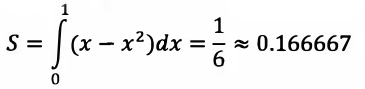Функция, вычисляющая площади разных геометрических фигур
Функция, вычисляющая площади разных геометрических фигур.
Допустим, требуется написать функцию, которая может вычислять площадь
круга, прямоугольника и треугольника и.т.д. Площадь какой фигуры
необходимо вычислить, должно определяться передаваемыми аргументами.
Напишите программу, вычисляющую площади геометрических фигур
Помогите пожалуйста:"Напишите программу, вычисляющую площади геометрических фигур – треугольника.
Вычисление площади разных геометрических фигур !
Создать модуль пользователя,что содержит функции и процедуры с помощью которых можно рассчитать.
Вычисление площади геометрических фигур
Помогите пожалуйста ! Задача: организовать вычисление площади геометрических фигур. Выбор фигуры.
Вычисление площади, периметра геометрических фигур
Почему у меня ошибка program n_666; const pi=3.14; var a, b, h, s, c, p, k, z, d, r: real;.
Вычислить площади различных геометрических фигур
Вычислить площади различных геометрических фигур и вывести на печать их наименование. .
1 2 3 4 5 6 7 8 9 10 11 12 13 14
def area(figure, data): if figure == 'круг': print(data[0]) res = 3.14*(data[0]**2) if figure == 'квадрат': a,b = data res = a*b if figure == 'треугольник': res = (a*b)/2 return ' Площадь <> = <>'.format(figure, res) figure = input('фигура >>> ') data = [ float(i) for i in input('данные через пробел >>> ').split()] print(area(figure, data))
Найти площадь прямоугольника, треугольника или круга
В зависимости от того, что выберет пользователь, вычислить площадь либо прямоугольника, либо треугольника, либо круга. Если выбраны прямоугольник или треугольник, то надо запросить длины сторон, если круг, то его радиус.
Решение задачи на языке программирования Python
Площадь треугольника вычисляется по формуле Герона:
, где p — это полупериметр, a , b , c — длины сторон. Полупериметр равен половине периметра, то есть половине суммы сторон.
Площадь прямоугольника равна произведению его двух сторон (длины и ширины). Площадь круга вычисляется по формуле S = πr 2 .
from math import sqrt, pi print("1-прямоугольник, 2-треугольник, 3-круг") figure = input("Выберите фигуру: ") if figure == '1': print("Длины сторон прямоугольника:") a = float(input("a = ")) b = float(input("b = ")) print("Площадь: %.2f" % (a * b)) elif figure == '2': print("Длины сторон треугольника:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) p = (a + b + c) / 2 s = sqrt(p * (p - a) * (p - b) * (p - c)) print("Площадь: %.2f" % s) elif figure == '3': r = float(input("Радиус круга R = ")) print("Площадь: %.2f" % (pi * r ** 2)) else: print("Ошибка ввода")
Пример выполнение программы:
1-прямоугольник, 2-треугольник, 3-круг Выберите фигуру: 2 Длины сторон треугольника: a = 4 b = 5 c = 6 Площадь: 9.92
Начиная с версии 3.10, в Python имеется оператор match . Вариант решения задачи с его помощью будет выглядеть так:
from math import sqrt, pi print("1-прямоугольник, 2-треугольник, 3-круг") figure = input("Выберите фигуру: ") match figure: case '1': print("Длины сторон прямоугольника:") a = float(input("a = ")) b = float(input("b = ")) print("Площадь: %.2f" % (a * b)) case '2': print("Длины сторон треугольника:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) p = (a + b + c) / 2 s = sqrt(p * (p - a) * (p - b) * (p - c)) print("Площадь: %.2f" % s) case '3': r = float(input("Радиус круга R = ")) print("Площадь: %.2f" % (pi * r ** 2)) case _: print("Ошибка ввода")
Напишите программу, вычисляющую площади геометрических фигур
Помогите пожалуйста:»Напишите программу, вычисляющую площади геометрических фигур – треугольника, трапеции, эллипса. Окно должно содержать виджет выбора фигуры, поле ввода необходимых числовых характеристик фигуры, поле вывода значения площади, кнопка расчета, кнопка выхода.»
Использовать по возможности простые, пусть и не рациональные, функции.
Функция, вычисляющая площади разных геометрических фигур
Функция, вычисляющая площади разных геометрических фигур. Допустим, требуется написать функцию.
Вычисление площади геометрических фигур
Помогите пожалуйста ! Задача: организовать вычисление площади геометрических фигур. Выбор фигуры.
Вычислить площади различных геометрических фигур
Вычислить площади различных геометрических фигур и вывести на печать их наименование. .
Вычисление площади, периметра геометрических фигур
Почему у меня ошибка program n_666; const pi=3.14; var a, b, h, s, c, p, k, z, d, r: real;.
Сообщение было отмечено Dmitriy+ как решение
Решение
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
from collections import namedtuple from math import sqrt, pi # Side lengths Triangle = namedtuple("Triangle", "a b c") # Top and bottom length and height Trapezoid = namedtuple("Trapezoid", "a b h") # One-half of the ellipse's major and minor axes Ellipse = namedtuple("Ellipse", "a b") def triangle_area(triangle): """ [url]http://en.wikipedia.org/wiki/Heron%27s_formula[/url] """ p = (triangle.a + triangle.b + triangle.c) / 2 return sqrt(p * (p - triangle.a) * (p - triangle.b) * (p - triangle.c)) def trapezoid_area(trapezoid): return (trapezoid.a + trapezoid.b) * trapezoid.h / 2 def ellipse_area(ellipse): return pi * ellipse.a * ellipse.b def input_triangle(): a = input("a = ") b = input("b = ") c = input("c = ") return Triangle(float(a), float(b), float(c)) def input_trapezoid(): a = input("a = ") b = input("b = ") h = input("h = ") return Trapezoid(float(a), float(b), float(h)) def input_ellipse(): a = input("a = ") b = input("b = ") return Ellipse(float(a), float(b)) inputs = {1: input_triangle, 2: input_trapezoid, 3: input_ellipse} areas = {1: triangle_area, 2: trapezoid_area, 3: ellipse_area} def calculate_area(): figure_number = int(input("Input 1 to choose triangle, 2 - trapezoid, 3 - ellipse: ")) figure = inputs[figure_number]() area = areas[figure_number](figure) print(str.format(" area is ", figure, area)) def main(): while True: try: calculate_area() except Exception as e: print(e) print("Exit") break main()
Вычисление площади фигуры, ограниченной двумя кривыми с помощью Python
4 июня 2016 г. 
Archy 
Просмотров: 21156 
RSS 
Обсудить 
алгоритм вычисление площади фигуры python, вычисление площади python, вычисление площади фигуры python
Следующий пример, который мы рассмотрим — задача о вычислении площади фигуры, ограниченной двумя кривыми. Здесь, в этом примере, мы используем вложенные операторы цикла(то есть один оператор цикла вызывается в теле другого оператора цикла).
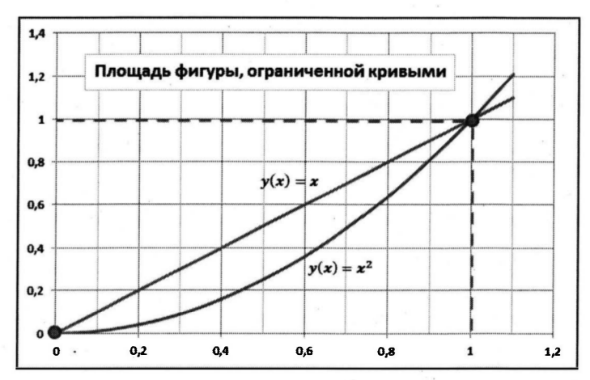
Что касается непосредственно решаемой задачи, то нам предстоит вычислить площадь фигуры, которая ограничена двумя кривыми, уравнения которых y(x) = x и y(x) = x^2. Графики этих кривых представлены на рис. 1.
Это прямая линия и парабола. Кривые пересекаются в двух точках: в точке x = 0, y = 0 и в точке x = 1, y = 1(точки определяются как решение уравнения x = x^2). Получается такой своеобразный «лепесток», площадь которого нам и предстоит вычислить.
Наша задача имеет точное решение. А именно, площадь S указанной фигуры следующая:
Однако мы будем использовать несколько иной подход.
Рис. 1. Вычисление области фигуры, ограниченной двумя кривыми
Метод, который описывается далее и применяется нами для вычисления площади фигуры, имеет отношение к теории вероятностей и математической статистике(обычно такой подход называют методами Монте-Карло).
При вычислении площади фигуры мы будем исходить из следующих соображений. Во-первых, замечаем, что область ограниченная кривыми, полностью попадает в единичный квадрат с левой нижней вершиной в точке начала координат и правой верхней вершиной в точке с единичными координатами. Если мы случайным образом выберем точку внутри этого квадрата, то она с некоторой вероятностью попадает в область, что ограничена кривыми (то есть попадает внутрь «лепестка»).
Теория вероятностей утверждает, что эта самая вероятность равна отношению площадей «лепестка» и квадрата. У квадрата с единичной стороной площадь равна единице. Поэтому площадь «лепестка»(которую нам необходимо вычислить) равняется вероятности, с которой случайным образом выбранная точка попадает внутрь «лепестка». Это будет «во вторых».
В третьих, если взять очень много случайных точек, равномерно распределенных по квадрату, и вычислить отношение количества точек внутри «лепестка» к общему количеству точек, в идеале получим оценку, близкую к вероятности попадания случайно выбранной точки внутрь «лепестка».
Мы всю эту процедуру немного модифицируем и поступим следующим образом. Вместо того чтобы генерировать случайны точки, покроем весь квадрат равноотстоящими узловыми точками. Посчитаем, сколько их попало внутрь «лепестка»(то есть области, ограниченной кривыми), и поделим на общее количество точек. Это и будет результат.
Программный код, в котором реализован такой подход, представлен ниже:
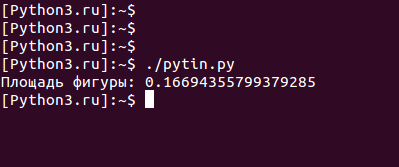
#!/usr/bin/env python3 # -*- coding: utf-8 -*- # Количество равных интервалов, на которые # делятся стороны единичного квадрата n = 500 # "Цена деления" - расстояние между соседними точками dz = 1 / n; # Количество точек, которые попадают внутрь области pts = 0 # Начальное значение индекса, определяющего столбец точек i = 0 # Внешний оператор цикла. Перебираем столбцы точек while i = x**2: # Еще одна точка внутри области pts += 1 # Значение второго индекса увеличиваем на единицу j += 1 # Значение первого индекса увеличиваем на единицу i += 1 # Вычисляем площадь фигуры S = pts / (n + 1) ** 2 # Отображаем результат print("Площадь фигуры: " + str(S)) Результат, который приведен ниже, достаточно близок к точному решению:
Чтобы понять логику вычислений, имеет смысл мысленно представить, как мы разбиваем каждую из сторон квадрата на определенное количество интервалов. Количество этих интервалов записывается в переменную n(то есть значение 500).
Границу интервалов будем называть узловыми точками. Через каждую узловую точку на сторонах квадрата проводим горизонтальные и вертикальные линии. Точки пересечений этих линий — это именно те точки, которые нам нужны. Каждую такую точку можно «идентифицировать» с помощью двух индексов.
Первый индекс определяет узловую точку по горизонтали, а второй — узловую точку по вертикали. На пересечении линий, проходящих через эти узловых точки, находится «идентифицируемая» точка внутри квадрата.
Если мы зафиксируем первый индекс, и будем брать разные значения для второго индекса, то все соответствующие точки будут находится на одной вертикальной прямой. Про такие точки будем говорить, что они находятся в одном столбце. Если зафиксировать второй индекс и брать разные значения первого индекса, то все соответствующие точки будут находиться на одной горизонтальной прямой. Про такие точки можем говорить, что они формируют ряд точек.
В каждому ряду и в каждом столбце размещено ровно n + 1 точек ( если учитывать и те точки, что находятся на координатных осях).
Расстояние (по горизонтали или по вертикали) между двумя соседними узловыми точками равняется, очевидно, единице, деленной на количество интервалов, на которые разбивалась каждая из сторон квадрата: такая «цена деления» записывается в переменную dz(значение 1/n). В переменную pts(начальное значение 0) будем записывать количество точек, которые попали внутрь «лепестка».
В условном операторе проверяется условие y = x**2. Это и есть условие попадания точки с координатами X(переменная x) и Y(переменная y) внутрь области, ограниченной кривыми y = x и y = x ^ 2. Чтобы точка попадала в это область, необходимо чтобы одновременно выполнялись два условия. Во-первых, точка должна находиться ниже прямой y = x, а это имеет место, если y = x ^ 2. Следовательно, должно выполняться соотношение x ^ 2 = x**2. Кстати, вместо инструкции y = x**2 вполне законно можно было использовать выражение x ** 2