Python opencv detect rectangle

How to detect a rectangle and square in an image using OpenCV Python?

To detect a rectangle and square in an image, we first detect all the contours in the image. Then Loop over all contours. Find the approximate contour for each of the contours. If the number of vertex points in the approximate contour is 4 then we compute the aspect ratio to make a difference between the rectangle and square. If the aspect ratio is between 0.9 and 1.1 we say it is a square else a rectangle See the below pseudocode.

for cnt in contours: approx = cv2.approxPolyDP(cnt) if len(approx) == 4: x, y, w, h = cv2.boundingRect(cnt) ratio= float(w)/h if ratio>=0.9 and ratio
Steps
You can use the following steps to detect a rectangle and a square in the input image −
Import the required library. In all the following Python examples, the required Python library is OpenCV. Make sure you have already installed it.
Read the input image using cv2.imread() and convert it to grayscale.
img = cv2.imread('shapes.jpg') gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
 
Apply thresholding on the grayscale image to create a binary image. Adjust the second parameter to get a better contour detection.
 
ret,thresh = cv2.threshold(gray,50,255,0)
 
Find the contours in the image using cv2.findContours() function.
 
contours, _ = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
 
Select a contour (say first contour) cnt from the lists of contours. Or loop over all the contours.
 
Compute the approximate contour points for each contour cnt using cv2.approxPolyDP() function
 
approx = cv2.approxPolyDP(cnt,epsilon,True)
 
If the vertex points in the approximate contour approx is 4, then draw the contour on the image.
 
Compute the aspect ratio of the contour cnt. Set a range of aspect ratios to detect the square. We set it [0.9, 1.1]. If the ratio is between 0.9 and 1.1, the detected contour is a square else it is a rectangle.
 
Display the image with detected rectangle and square and drawn contours.
 
cv2.imshow("Shapes", img) cv2.waitKey(0) cv2.destroyAllWindows()
 
Let's look at some examples for clear understanding.
 
Example
 
In the Python code below, we detect the rectangle and square in the input image.
 
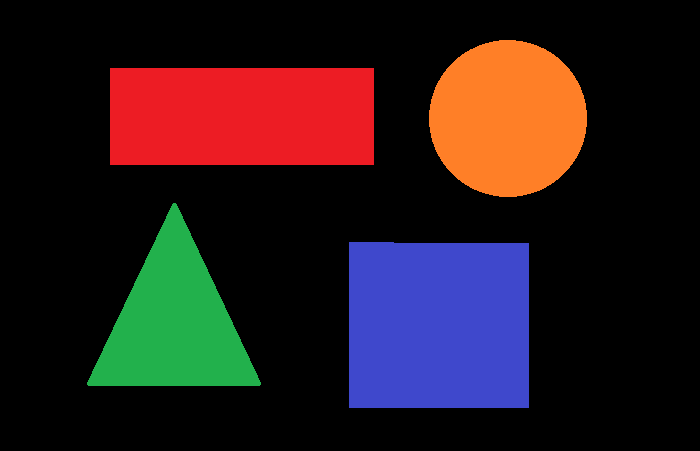
import cv2 import numpy as np img = cv2.imread('shapes.jpg') gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) ret,thresh = cv2.threshold(gray,50,255,0) contours,hierarchy = cv2.findContours(thresh, 1, 2) print("Number of contours detected:", len(contours)) for cnt in contours: x1,y1 = cnt[0][0] approx = cv2.approxPolyDP(cnt, 0.01*cv2.arcLength(cnt, True), True) if len(approx) == 4: x, y, w, h = cv2.boundingRect(cnt) ratio = float(w)/h if ratio >= 0.9 and ratio  1.1: img = cv2.drawContours(img, [cnt], -1, (0,255,255), 3) cv2.putText(img, 'Square', (x1, y1), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (255, 255, 0), 2) else: cv2.putText(img, 'Rectangle', (x1, y1), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2) img = cv2.drawContours(img, [cnt], -1, (0,255,0), 3) cv2.imshow("Shapes", img) cv2.waitKey(0) cv2.destroyAllWindows() 
 
Consider the following image as the Input File in the above program code.
 
 
Output
 
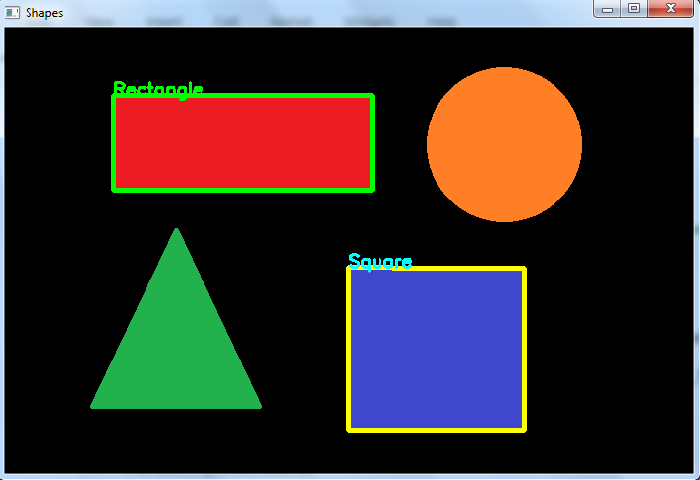
When you execute the above code, it will produce the following output.
 
Number of contours detected: 4
 
And we get the following window, showing the output −
 
 
In the above output image, one rectangle and one square are detected.
 
Источник
 
OpenCV на python: поиск прямоугольников и эллипсов
 
Разобравшись с выделением контуров объектов на видео, перейдем к более сложной задаче — обнаружению прямоугольников и эллипсов. Более того, мы не только научимся находить их в кадре, но еще и сможем определять угол их наклона!
 
Хорошим примером использования подобных алгоритмов может стать ситуация, когда роботу нужно правильно ухватиться за предмет. Прямо как на картинке.
 
 
Если смотреть на цилиндр сверху, то он превратится в прямоугольник. Зная его координаты в кадре и угол наклона можно рассчитать поворот схвата манипулятора, чтобы правильно ухватиться за предмет.
 
 
Функция OpenCV для поиска прямоугольников minAreaRect
 
Функция OpenCV для поиска эллипсов fitEllipse
 
Отсечение лишних контуров по площади
 
Вычисление угла поворота прямоугольника в OpenCV
 
Определение угла поворота прямоугольника в видеопотоке
 
 
1. Функция OpenCV для поиска прямоугольников minAreaRect
 
В OpenCV имеется функция, которая пытается найти прямоугольник максимального размера, который может вписаться в заданный замкнутый контур. Надо заметить, что эта функция не определяет является ли контур прямоугольным, она пытается вписать в него прямоугольник оптимальным способом. Это важно!
 
контур — это контур, в который мы собираемся вписать прямоугольник (тип аргумента — Nx2 массив NumPy).
 
Напишем программу, которая найдет на картинке все прямоугольники. За основу возьмем код из предыдущего урока про поиск контуров.
 
#!/usr/bin/env python import sys import numpy as np import cv2 as cv hsv_min = np.array((0, 54, 5), np.uint8) hsv_max = np.array((187, 255, 253), np.uint8) if __name__ == '__main__': fn = 'image2.jpg' # имя файла, который будем анализировать img = cv.imread(fn) hsv = cv.cvtColor( img, cv.COLOR_BGR2HSV ) # меняем цветовую модель с BGR на HSV thresh = cv.inRange( hsv, hsv_min, hsv_max ) # применяем цветовой фильтр _, contours0, hierarchy = cv.findContours( thresh.copy(), cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE) # перебираем все найденные контуры в цикле for cnt in contours0: rect = cv.minAreaRect(cnt) # пытаемся вписать прямоугольник box = cv.boxPoints(rect) # поиск четырех вершин прямоугольника box = np.int0(box) # округление координат cv.drawContours(img,[box],0,(255,0,0),2) # рисуем прямоугольник cv.imshow('contours', img) # вывод обработанного кадра в окно cv.waitKey() cv.destroyAllWindows()
 
Результат работы программы:
 
 
 
Видно, что алгоритм попытался вписать прямоугольники во вложенные мусорные контуры на самих объектах. Далее мы разберемся как с этим бороться.
 
Теперь попробуем тоже самое, но с эллипсами.
 
2. Функция OpenCV для поиска эллипсов fitEllipse
 
Как и в случае minAreaRect, функция поиска эллипсов не сможет отличить на картинке объект с действительно эллиптическим контуром от квадрата. Она лишь пытается эллипс вписать в любой контур с количеством точек >=5.
 
контур — это контур, в который мы собираемся вписать прямоугольник (тип аргумента — Nx2 массив NumPy).
 
Слегка изменим предыдущую программу, убрав из неё minAreaRect и добавив fitEllipse.
 
#!/usr/bin/env python import sys import numpy as np import cv2 as cv hsv_min = np.array((0, 77, 17), np.uint8) hsv_max = np.array((208, 255, 255), np.uint8) if __name__ == '__main__': fn = 'donuts.jpg' img = cv.imread(fn) hsv = cv.cvtColor( img, cv.COLOR_BGR2HSV ) thresh = cv.inRange( hsv, hsv_min, hsv_max ) _, contours0, hierarchy = cv.findContours( thresh.copy(), cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE) for cnt in contours0: if len(cnt)>4: ellipse = cv.fitEllipse(cnt) cv.ellipse(img,ellipse,(0,0,255),2) cv.imshow('contours', img) cv.waitKey() cv.destroyAllWindows()
 
необходимо для того, чтобы отсечь контуры с контурами меньше 5 точек. Результат работы программы:
 
 
 
Надо заметить, что эллипсы лучше пытаться вписать в округлые объекты, а прямоугольники в прямоугольные:) В противном случае, алгоритм может выдать неадекватные результаты.
 
3. Отсечение лишних контуров по площади
 
Следующий шаг — разберемся с паразитными микроконтурами, которые мы обнаружили на объектах. Избавиться от них можно, вычислив площадь занимаемую этими контурами, а затем просто отсечь контуры с маленькой площадью.
 
Внесем в нашу программу модификацию:
 
box = np.int0(box) # округление координат area = int(rect[1][0]*rect[1][1]) # вычисление площади if area > 500: cv.drawContours(img,[box],0,(255,0,0),2)
 
 
 
4. Вычисление угла поворота прямоугольника в OpenCV
 
Наконец, вычислим углы наклона всех прямоугольников относительно горизонта. Здесь нам не понадобятся специальные функции OpenCV, достаточно будет простой математики.
 
#!/usr/bin/env python import sys import numpy as np import cv2 as cv import math hsv_min = np.array((0, 54, 5), np.uint8) hsv_max = np.array((187, 255, 253), np.uint8) color_blue = (255,0,0) color_yellow = (0,255,255) if __name__ == '__main__': fn = 'image2.jpg' # имя файла, который будем анализировать img = cv.imread(fn) hsv = cv.cvtColor( img, cv.COLOR_BGR2HSV ) # меняем цветовую модель с BGR на HSV thresh = cv.inRange( hsv, hsv_min, hsv_max ) # применяем цветовой фильтр _, contours0, hierarchy = cv.findContours( thresh.copy(), cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE) # перебираем все найденные контуры в цикле for cnt in contours0: rect = cv.minAreaRect(cnt) # пытаемся вписать прямоугольник box = cv.boxPoints(rect) # поиск четырех вершин прямоугольника box = np.int0(box) # округление координат center = (int(rect[0][0]),int(rect[0][1])) area = int(rect[1][0]*rect[1][1]) # вычисление площади # вычисление координат двух векторов, являющихся сторонам прямоугольника edge1 = np.int0((box[1][0] - box[0][0],box[1][1] - box[0][1])) edge2 = np.int0((box[2][0] - box[1][0], box[2][1] - box[1][1])) # выясняем какой вектор больше usedEdge = edge1 if cv.norm(edge2) > cv.norm(edge1): usedEdge = edge2 reference = (1,0) # горизонтальный вектор, задающий горизонт # вычисляем угол между самой длинной стороной прямоугольника и горизонтом angle = 180.0/math.pi * math.acos((reference[0]*usedEdge[0] + reference[1]*usedEdge[1]) / (cv.norm(reference) *cv.norm(usedEdge))) if area > 500: cv.drawContours(img,[box],0,(255,0,0),2) # рисуем прямоугольник cv.circle(img, center, 5, color_yellow, 2) # рисуем маленький кружок в центре прямоугольника # выводим в кадр величину угла наклона cv.putText(img, "%d" % int(angle), (center[0]+20, center[1]-20), cv.FONT_HERSHEY_SIMPLEX, 1, color_yellow, 2) cv.imshow('contours', img) cv.waitKey() cv.destroyAllWindows()
 
Помним, что цветовые фильтры hsv_min и hsv_max нужно каждый раз настраивать под конкретный объект и освещение!
 
Запускаем программу, указав в ней в качестве исходного — изображение с макетными платами.
 
 
 
Ура! Работает. Ну и последний шаг — подключим видеопоток.
 
5. Определение угла поворота прямоугольника в видеопотоке
 
#!/usr/bin/env python import cv2 as cv import numpy as np import video import math if __name__ == '__main__': cv.namedWindow( "result" ) cap = video.create_capture(0) hsv_min = np.array((0, 0, 255), np.uint8) hsv_max = np.array((72, 51, 255), np.uint8) color_blue = (255,0,0) color_red = (0,0,128) while True: flag, img = cap.read() img = cv.flip(img,1) try: hsv = cv.cvtColor(img, cv.COLOR_BGR2HSV ) thresh = cv.inRange(hsv, hsv_min, hsv_max) _, contours0, hierarchy = cv.findContours( thresh.copy(), cv.RETR_EXTERNAL, cv.CHAIN_APPROX_NONE) for cnt in contours0: rect = cv.minAreaRect(cnt) box = cv.boxPoints(rect) box = np.int0(box) center = (int(rect[0][0]),int(rect[0][1])) area = int(rect[1][0]*rect[1][1]) edge1 = np.int0((box[1][0] - box[0][0],box[1][1] - box[0][1])) edge2 = np.int0((box[2][0] - box[1][0], box[2][1] - box[1][1])) usedEdge = edge1 if cv.norm(edge2) > cv.norm(edge1): usedEdge = edge2 reference = (1,0) # horizontal edge angle = 180.0/math.pi * math.acos((reference[0]*usedEdge[0] + reference[1]*usedEdge[1]) / (cv.norm(reference) *cv.norm(usedEdge))) if area > 500: cv.drawContours(img,[box],0,color_blue,2) cv.circle(img, center, 5, color_red, 2) cv.putText(img, "%d" % int(angle), (center[0]+20, center[1]-20), cv.FONT_HERSHEY_SIMPLEX, 1, color_red, 2) cv.imshow('result', img) except: cap.release() raise ch = cv.waitKey(5) if ch == 27: break cap.release() cv.destroyAllWindows()
 
Помним про правильную настройку фильтров! Если всё сделано правильно, получится примерно это:
 
Your browser does not support the video tag. 
К размышлению
 
Итак, хорошая новость — мы умеем определять угол наклона прямоугольника. Плохая новость — мы не можем быть уверены, что в кадре именно прямоугольник! Та же ситуация с эллипсом. Попробуем разобраться с более продвинутыми методами детектирования геометрических объектов на следующих уроках!
 
Источник
 
Читайте также:  Python windows vista 32 bit