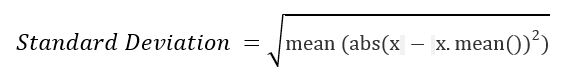numpy.std
Вычислите стандартное отклонение вдоль указанной оси.
Возвращает стандартное отклонение-меру распределения,элементов массива.По умолчанию среднеквадратическое отклонение вычисляется для сплющенного массива,в противном случае-по заданной оси.
Parameters aarray_like
Рассчитайте стандартное отклонение этих значений.
ось Нет, целое число или кортеж целых чисел, необязательно
Оси или оси,по которым рассчитывается стандартное отклонение.По умолчанию вычисляется стандартное отклонение сплющенного массива.
Если это кортеж из интв,то стандартное отклонение выполняется по нескольким осям,а не по одной оси или по всем осям,как раньше.
dtypedtype, optional
Тип для использования при вычислении стандартного отклонения.Для массивов целочисленного типа по умолчанию используется float64,для массивов типа float-тип массива.
outndarray, optional
Альтернативный выходной массив,в который помещать результат.Он должен иметь ту же форму,что и ожидаемый результат,но при необходимости будет приведен тип (из вычисленных значений).
ddofint, optional
Означает дельта степеней свободы. В расчетах используется делитель N — ddof , где N представляет собой количество элементов. По умолчанию ddof равен нулю.
keepdimsbool, optional
Если установлено значение True,то редуцированные оси останутся в результате в виде размеров с первым размером.При выборе этого параметра результат будет корректно отображаться на входном массиве.
Если передано значение по умолчанию, то keepdims не будут переданы методу std подклассов ndarray , однако любое значение, отличное от значения по умолчанию, будет передано. Если метод подкласса не реализует keepdims , будут вызваны любые исключения.
где array_like of bool, необязательно
Элементы для включения в стандартное отклонение. Подробности см. В разделе » reduce .
Если out равно None, вернуть новый массив, содержащий стандартное отклонение, в противном случае вернуть ссылку на выходной массив.
Notes
Стандартное отклонение — это квадратный корень из среднего квадрата отклонений от среднего, т. x = abs(a — a.mean())**2 std = sqrt(mean(x)) , где x = abs (a — a.mean ()) ** 2 .
Среднее квадратическое отклонение обычно рассчитывается как x.sum() / N , где N = len(x) . Если, однако, ddof указывается, делитель N — ddof используется вместо этого. В стандартной статистической практике ddof=1 обеспечивает несмещенную оценку дисперсии бесконечной совокупности. ddof=0 обеспечивает оценку максимального правдоподобия дисперсии для нормально распределенных переменных. Стандартное отклонение, вычисленное в этой функции, является квадратным корнем из оцененной дисперсии, поэтому даже при ddof=1 это не будет объективной оценкой стандартного отклонения как такового.
Обратите внимание, что для комплексных чисел std принимает абсолютное значение перед возведением в квадрат, поэтому результат всегда действительный и неотрицательный.
Для ввода с плавающей запятой std вычисляется с той же точностью, что и ввод. В зависимости от входных данных это может привести к неточности результатов, особенно для float32 (см. Пример ниже). Указание аккумулятора более высокой точности с помощью dtype слова dtype может решить эту проблему.
Examples
>>> a = np.array([[1, 2], [3, 4]]) >>> np.std(a) 1.1180339887498949 # may vary >>> np.std(a, axis=0) array([1., 1.]) >>> np.std(a, axis=1) array([0.5, 0.5])
При одинаковой точности std()может быть неточным:
>>> a = np.zeros((2, 512*512), dtype=np.float32) >>> a[0, :] = 1.0 >>> a[1, :] = 0.1 >>> np.std(a) 0.45000005
Вычисление стандартного отклонения в float64 более точное:
>>> np.std(a, dtype=np.float64) 0.44999999925494177 # may vary
>>> a = np.array([[14, 8, 11, 10], [7, 9, 10, 11], [10, 15, 5, 10]]) >>> np.std(a) 2.614064523559687 # may vary >>> np.std(a, where=[[True], [True], [False]]) 2.0
Statistics#
Compute the q-th percentile of the data along the specified axis.
Compute the qth percentile of the data along the specified axis, while ignoring nan values.
quantile (a, q[, axis, out, overwrite_input, . ])
Compute the q-th quantile of the data along the specified axis.
Compute the qth quantile of the data along the specified axis, while ignoring nan values.
Averages and variances#
median (a[, axis, out, overwrite_input, keepdims])
Compute the median along the specified axis.
average (a[, axis, weights, returned, keepdims])
Compute the weighted average along the specified axis.
mean (a[, axis, dtype, out, keepdims, where])
Compute the arithmetic mean along the specified axis.
std (a[, axis, dtype, out, ddof, keepdims, where])
Compute the standard deviation along the specified axis.
var (a[, axis, dtype, out, ddof, keepdims, where])
Compute the variance along the specified axis.
nanmedian (a[, axis, out, overwrite_input, . ])
Compute the median along the specified axis, while ignoring NaNs.
nanmean (a[, axis, dtype, out, keepdims, where])
Compute the arithmetic mean along the specified axis, ignoring NaNs.
Compute the standard deviation along the specified axis, while ignoring NaNs.
Compute the variance along the specified axis, while ignoring NaNs.
Correlating#
corrcoef (x[, y, rowvar, bias, ddof, dtype])
Return Pearson product-moment correlation coefficients.
Cross-correlation of two 1-dimensional sequences.
cov (m[, y, rowvar, bias, ddof, fweights, . ])
Estimate a covariance matrix, given data and weights.
Histograms#
histogram (a[, bins, range, density, weights])
Compute the histogram of a dataset.
Compute the bi-dimensional histogram of two data samples.
histogramdd (sample[, bins, range, density, . ])
Compute the multidimensional histogram of some data.
Count number of occurrences of each value in array of non-negative ints.
Function to calculate only the edges of the bins used by the histogram function.
Return the indices of the bins to which each value in input array belongs.
Функция Numpy std() в Python
Стандартное отклонение – это мера, на которую элементы набора отклоняются или расходятся от среднего значения.
В Numpy вы можете найти стандартное отклонение массива Numpy, используя функцию numpy.std().
Мы рассмотрим примеры, охватывающие различные скрипты, чтобы понять использование функции numpy std().
Пример 1
В этом примере мы возьмем массив Numpy 1D с тремя элементами и найдем стандартное отклонение массива.
import numpy as np #initialize array A = np.array([2, 1, 6]) #compute standard deviation output = np.std(A) print(output)
Mean = (2 + 1 + 6)/3 = 3 Standard Deviation = sqrt( ((2-3)^2 + (1-3)^2 + (6-3)^2)/3 ) = sqrt( (1+4+9)/3 ) = sqrt(14/3) = sqrt(4.666666666666667) = 2.160246899469287
Пример 2: 2D-массив
В этом примере мы возьмем 2D-массив размером 2Ã – 2 и найдем стандартное отклонение массива.
import numpy as np #initialize array A = np.array([[2, 3], [6, 5]]) #compute standard deviation output = np.std(A) print(output)
Mean = (2 + 3 + 6 + 5)/4 = 4 Standard Deviation = sqrt( ((2-4)^2 + (3-4)^2 + (6-4)^2 + (5-4)^2)/4 ) = sqrt( (4+1+4+1)/4 ) = sqrt(10/4) = sqrt(2.5) = 1.5811388300841898
Пример 3: вдоль оси
Вы также можете найти стандартное отклонение массива Numpy по оси.
В этом примере мы возьмем Numpy 2D-массив размером 2Ã – 2 и найдем стандартное отклонение массива вдоль оси.
import numpy as np #initialize array A = np.array([[2, 3], [6, 5]]) #compute standard deviation output = np.std(A, axis=0) print(output)
1st element ====================== mean = (2+6)/2 = 4 standard deviation = sqrt( ( (2-4)^2 + (6-4)^2 )/2 ) = sqrt( 4 ) = 2.0 2nd element ====================== mean = (3+5)/2 = 4 standard deviation = sqrt( ( (3-4)^2 + (5-4)^2 )/2 ) = sqrt( 1 ) = 1.0
numpy.std() in Python
numpy.std(arr, axis = None) : Compute the standard deviation of the given data (array elements) along the specified axis(if any)..
Standard Deviation (SD) is measured as the spread of data distribution in the given data set.
For example :
x = 1 1 1 1 1 Standard Deviation = 0 . y = 9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4 Step 1 : Mean of distribution 4 = 7 Step 2 : Summation of (x - x.mean())**2 = 178 Step 3 : Finding Mean = 178 /20 = 8.9 This Result is Variance. Step 4 : Standard Deviation = sqrt(Variance) = sqrt(8.9) = 2.983..
Parameters :
arr : [array_like]input array.
axis : [int or tuples of int]axis along which we want to calculate the standard deviation. Otherwise, it will consider arr to be flattened (works on all the axis). axis = 0 means SD along the column and axis = 1 means SD along the row.
out : [ndarray, optional]Different array in which we want to place the result. The array must have the same dimensions as expected output.
dtype : [data-type, optional]Type we desire while computing SD.Results : Standard Deviation of the array (a scalar value if axis is none) or array with standard deviation values along specified axis.