Python нахождение производной функции

Дифференцирование и интегрирование функций#

В рамказ компьютерной арифметики предельный переход осуществить невозможно, поэтому в целях аппроксимации производной нередко вместо предела при \(h \to 0\) подставляют очень малое \(h\) :

Такая аппроксимация производной называется правой разностной производной. Можно показать, что асимптотическая погрешность вычисления производной таким способом имеет вид \(o(h)\) , т.е. уменьшая шаг \(h\) можно добиться любой точности вычисления производной. Более распространенна центральная разнастная производная, определяемая выражением

Её асимптотическая погрешность имеет вид \(o(h^2)\) , а значит уменьшая шаг \(h\) в 2 раза, можно ожидать уменьшение погрешности вычисления производной в 4 раза.

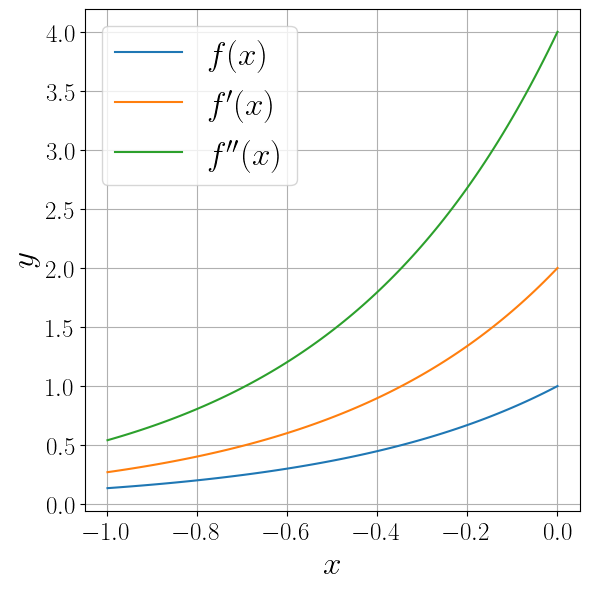
Аналогичным образом можно определить аппроксимацию производной любого порядка. Метод scipy.misc.derivative в SciPy вычисляет разностную производную произвольного порядка (опциональный параметр n ).

Продемонстрируем его применение на примере функции \(f(x) = e^\) .

from scipy.misc import derivative import numpy as np def f(x): return np.exp(2. * x) fig, ax = plt.subplots(figsize=(6, 6), layout="tight") x = np.linspace(-1, 0, 100) labels = ("$f(x)$", "$f'(x)$", "$f''(x)$") for n, label in enumerate(labels): y = derivative(f, x, n=n, dx=1e-3, order=2*n+1) if order > 0 else f(x) ax.plot(x, y, label=label) ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() ax.grid() 

Аналитическое дифференцирование#

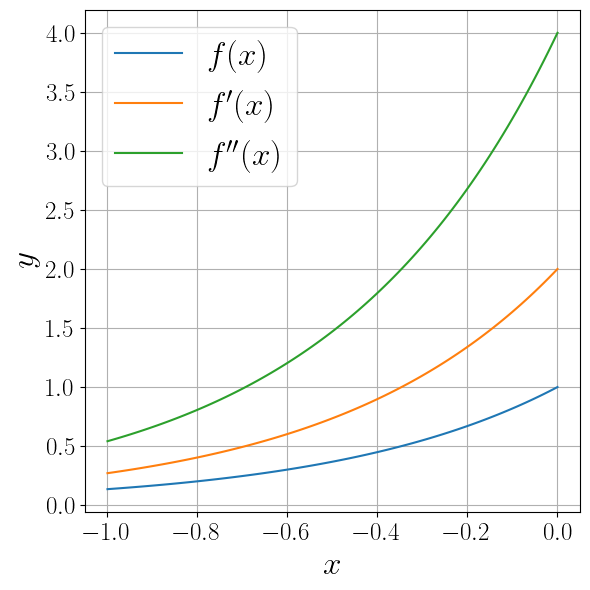
Ряд современных библиотек умеет вычислять производные от своих методов. Например, библиотека autograd.

Обратите внимание, что для аналитического вычисления производной средствами библиотеки autograd , необходимо вместо библиотеки NumPy использовать модуль autograd.numpy .

from autograd import numpy as np from autograd import elementwise_grad fig, ax = plt.subplots(figsize=(6, 6), layout="tight") x = np.linspace(-1, 0, 100) labels = ("$f(x)$", "$f'(x)$", "$f''(x)$") funcs = (f, elementwise_grad(f), elementwise_grad(elementwise_grad(f))) for order, (label, func) in enumerate(zip(labels, funcs)): ax.plot(x, func(x), label=label) ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() ax.grid() 

Интегрирование функций#

Подмодуль scipy.integrate позволяет приближенно вычислять значение определенных интегралов.

Однократные интегралы#

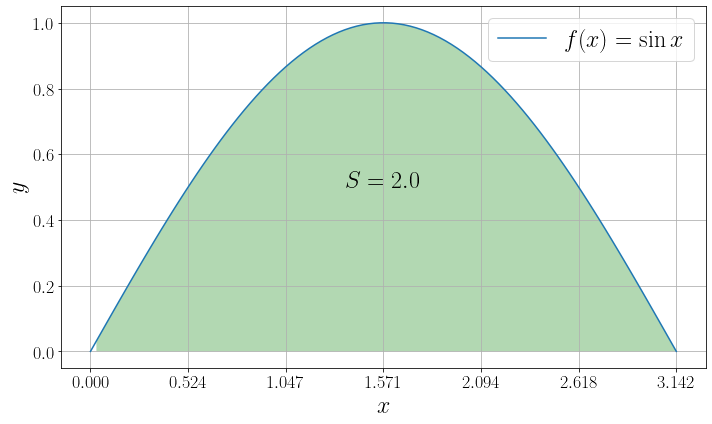
Функция scipy.integrate.quad позволяет проинтегрировать функцию \(f\colon \mathbb \to \mathbb\) . Вызов функции quad(f, a, b) приближенно находит значение интеграла

В качестве примера найдем численно значение интеграла

import numpy as np from scipy import integrate from matplotlib import pyplot as plt f = np.sin a, b = 0, np.pi I, _ = integrate.quad(f, 0, np.pi) x = np.linspace(0, np.pi, 100) y = f(x) fig, ax = plt.subplots(figsize=(10, 6), layout="tight") ax.plot(x, y, label=r"$f(x)=\sin x$") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.fill_between(x, np.zeros_like(x), y, where=(y>0), facecolor='green', alpha=0.30) ax.set_xticks(np.linspace(0, np.pi, 7)) ax.text(np.pi/2, 0.5, fr"$S = I>$", fontdict="size": 24, "ha": "center">) ax.legend() ax.grid() 

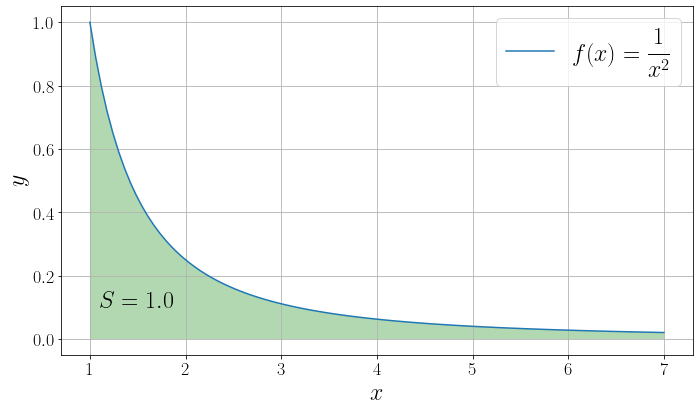
Параметры \(a\) и \(b\) могут принимать значения -inf и +inf , чтобы брать несобственные интегралы. Продемонстрируем это на примере интеграла

def f(x): return 1. / np.square(x) a, b = 1, np.inf I, _ = integrate.quad(f, a, b) x = np.linspace(a, 7, 100) y = f(x) fig, ax = plt.subplots(figsize=(10, 6), layout="tight") ax.plot(x, y, label=r"$f(x)=\dfrac $") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.fill_between(x, np.zeros_like(x), y, where=(y>0), facecolor='green', alpha=0.30) ax.set_xticks(np.linspace(1, 7, 7)) ax.text(1.5, 0.1, fr"$S = I>$", fontdict="size": 24, "ha": "center">) ax.legend() ax.grid() 

Однако численное взятие несобственных интегралов отнюдь не тривиальная задача. Например, интеграл Френеля $ \( \int\limits_0^\infty \sin x^2 \, dx = \sqrt<\dfrac<\pi>> \) $

просто так вычислить не удастся.

def f(t): return np.sin(t**2) I, _ = integrate.quad(f, 0, np.inf) print(I) 

C:\Users\fadeev\AppData\Local\Temp/ipykernel_8252/3166585030.py:4: IntegrationWarning: The integral is probably divergent, or slowly convergent. I, _ = integrate.quad(f, 0, np.inf)

Интегралы большей кратности#

Функция scipy.integrate.dblquad позволяет вычислять интегралы вида

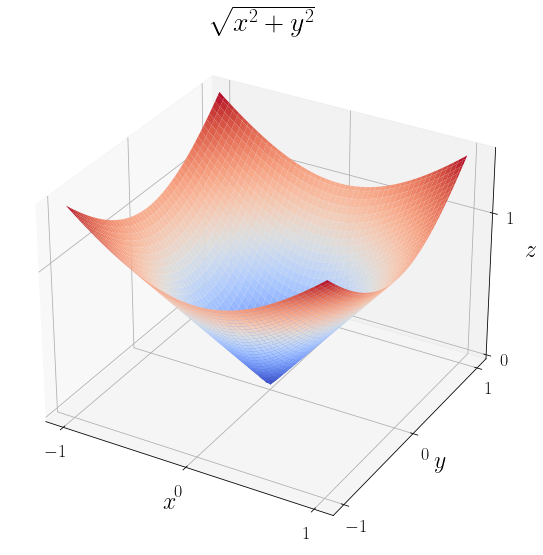
В качестве примера возьмём интеграл функции \(f = \sqrt\) в области \(D\) совпадающей с кругом единичного радиуса с центром в начале:

import numpy as np from scipy import integrate from matplotlib import pyplot as plt def h(x): return np.sqrt(1 - x**2) def g(x): return -h(x) def f(x, y): return np.sqrt(x**2 + y**2) a, b = -1, 1 I, _ = integrate.dblquad(f, -1, 1, g, h) x = np.linspace(a, b, 100) y = np.linspace(a, b, 100) x, y = np.meshgrid(x, y) z = f(x, y) fig, ax = plt.subplots(figsize=(8, 8), layout="tight", subplot_kw="projection": "3d">) ax.plot_surface(x, y, z, cmap="coolwarm") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.set_zlabel("$z$") ax.set_xticks([-1, 0, 1]) ax.set_yticks([-1, 0, 1]) ax.set_zticks([0, 1]) ax.set_title(r"$\sqrt$") print(f"Вычисленное значение интеграла: I>, точное значение: 2*np.pi/3>.") 

Вычисленное значение интеграла: 2.0943951023924106, точное значение: 2.0943951023931953.

Трехкратные интегралы вида

можно вычислить методом integrate.tplquad. Интеграл произвольной кратности можно вычислить методом integrate.tplquad.

Источник

Вычисление производной

Для вычисления производных будем использовать библиотеку SymPy. Это библиотека с открытым исходным кодом, полностью написанная на языке Python. Разрабатывается как система компьютерной алгебры.

Подключение SymPy

Вначале нам необходимо установить библиотеку. Для этого в терминале (командной строке) следует ввести команду: pip install sympy .

Для подключения библиотеки в коде на Python 3 следует использовать ключевое слово import .

Чтобы не писать перед всеми функциями sympy с точкой, подключу следующим образом:

Следует обратить внимание, что в SymPy объявлено множество классов и функций, имена которых могут пересекаться с названиями в других библиотеках. Например, если используете библиотеку math, то там также есть sin , cos , pi и другие.

Формула российских дорог

Например, возьмем функцию с двумя независимыми переменными, типа поверхности y=f(x, z). Воспользуемся формулой российских дорог: y=sin(x)+0,5·z.

Перед тем как взять производную этой функции в Python, надо объявить все переменные, которые будут использоваться в ней. Для этого следует воспользоваться функцией symbols . В качестве аргумента используем строку с перечисленными через запятую или пробел названиями переменных.

После этого берем частную производную в Python 3 с помощью функции diff . Первым аргументом пишем функцию, вторым – переменную, по которой будем её дифференцировать.

Результат выводим с помощью print .

Дорога в горку

from sympy import * x, z = symbols('x z') print(diff(sin(x)+0.5*z, z)) 0.500000000000000

В результате получили 0.5. Частная производная по z положительна, следовательно, дорога в горку.

Дорога с колеёй

Теперь возьмём производную по x:

from sympy import * x, z = symbols('x z') print(diff(sin(x)+0.5*z, x)) cos(x)

Получили, что частная производная по x равна cos(x). Трактору на колею наплевать, ему важен только наклон горки.

В зависимости от задачи берем производную по нужному параметру.

В функции diff при необходимости, можно указать третьим параметром порядок дифференцирования. Так как мы вычисляли производную первого порядка, то его не указывали.

Источник

Вычислить производную в Python

В этом руководстве представлены методы вычисления производной функции в Python.

Производная с библиотекой SymPy на Python

Библиотека SymPy известна как Python Symbolic library . Его можно использовать для выполнения сложных математических операций, таких как производные над функциями в Python. Функция diff() внутри библиотеки SymPy может использоваться для вычисления производной функции. Мы можем указать переменную, с которой мы хотим вычислить производную, с помощью функции Symbol() в Python. См. Следующий пример кода.

from sympy import * import numpy as np  x = Symbol('x') y = x**2 + 1  yprime = y.diff(x) print(yprime) 

В приведенном выше коде мы вычислили производную функции x^2 + 1 с помощью функции diff() библиотеки SymPy в Python. Мы задали символом x с помощью функции Symbol() и вычислили производную по символу x .

Maisam is a highly skilled and motivated Data Scientist. He has over 4 years of experience with Python programming language. He loves solving complex problems and sharing his results on the internet.

Сопутствующая статья — Python Math

Источник