- Matplotlib. Урок 4.3. Визуализация данных. Столбчатые и круговые диаграммы
- Столбчатые диаграммы
- Групповые столбчатые диаграммы
- Диаграмма с errorbar элементом
- Круговые диаграммы
- Классическая круговая диаграмма
- Вложенные круговые диаграммы
- Круговая диаграмма в виде бублика
- P.S.
- Examples#
- Lines, bars and markers#
- Images, contours and fields#
- Subplots, axes and figures#
- Statistics#
- Pie and polar charts#
- Text, labels and annotations#
- The pyplot module#
- Color#
- Shapes and collections#
- Style sheets#
- The axes_grid1 module#
- The axisartist module#
- Showcase#
- Animation#
- Event handling#
Matplotlib. Урок 4.3. Визуализация данных. Столбчатые и круговые диаграммы
В этому уроке изучим особенности работы со столбчатой и круговой диаграммами.
Столбчатые диаграммы
Для визуализации категориальных данных хорошо подходят столбчатые диаграммы. Для их построения используются функции:
bar() – для построения вертикальной диаграммы
barh() – для построения горизонтальной диаграммы.
Построим простую диаграмму:
np.random.seed(123) groups = [f"P" for i in range(7)] counts = np.random.randint(3, 10, len(groups)) plt.bar(groups, counts)
Если заменим bar() на barh() получим горизонтальную диаграмму:
Рассмотрим более подробно параметры функции bar() :
- x : набор величин
- x координаты столбцов
- Высоты столбцов
- Ширина столбцов
- y координата базы
- Выравнивание по координате x .
- color : скалярная величина, массив или optional
- Цвет столбцов диаграммы
- Цвет границы столбцов
- Ширина границы
- Метки для столбца
- Величина ошибки для графика. Выставленное значение удаляется/прибавляется к верхней (правой – для горизонтального графика) границе. Может принимать следующие значения:
- скаляр: симметрично +/- для всех баров
- shape(N,) : симметрично +/- для каждого бара
- shape(2,N) : выборочного – и + для каждого бара. Первая строка содержит нижние значения ошибок, вторая строка – верхние.
- None : не отображать значения ошибок. Это значение используется по умолчанию.
- Цвет линии ошибки.
- Включение логарифмического масштаба для оси y
- Ориентация: вертикальная или горизонтальная.
Построим более сложный пример, демонстрирующий работу с параметрами:
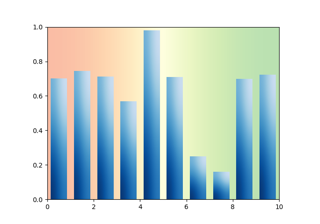
import matplotlib.colors as mcolors bc = mcolors.BASE_COLORS np.random.seed(123) groups = [f"P" for i in range(7)] counts = np.random.randint(0, len(bc), len(groups)) width = counts*0.1 colors = [["r", "b", "g"][int(np.random.randint(0, 3, 1))] for _ in counts] plt.bar(groups, counts, width=width, alpha=0.6, bottom=2, color=colors, edgecolor="k", linewidth=2)
Групповые столбчатые диаграммы
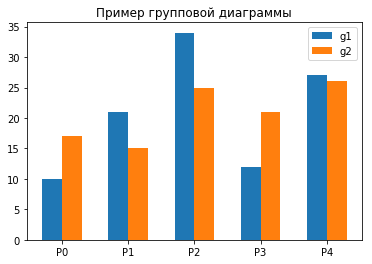
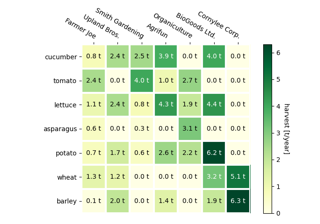
Используя определенным образом подготовленные данные можно строить групповые диаграммы:
cat_par = [f"P" for i in range(5)] g1 = [10, 21, 34, 12, 27] g2 = [17, 15, 25, 21, 26] width = 0.3 x = np.arange(len(cat_par)) fig, ax = plt.subplots() rects1 = ax.bar(x - width/2, g1, width, label='g1') rects2 = ax.bar(x + width/2, g2, width, label='g2') ax.set_title('Пример групповой диаграммы') ax.set_xticks(x) ax.set_xticklabels(cat_par) ax.legend()Диаграмма с errorbar элементом
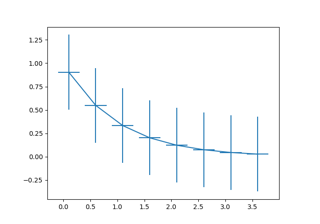
Errorbar элемент позволяет задать величину ошибки для каждого элемента графика. Для этого используются параметры xerr , yerr и ecolor (для задания цвета):
np.random.seed(123) rnd = np.random.randint cat_par = [f"P" for i in range(5)] g1 = [10, 21, 34, 12, 27] error = np.array([[rnd(2,7),rnd(2,7)] for _ in range(len(cat_par))]).T fig, axs = plt.subplots(1, 2, figsize=(10, 5)) axs[0].bar(cat_par, g1, yerr=5, ecolor="r", alpha=0.5, edgecolor="b", linewidth=2) axs[1].bar(cat_par, g1, yerr=error, ecolor="r", alpha=0.5, edgecolor="b", linewidth=2)
Круговые диаграммы
Классическая круговая диаграмма
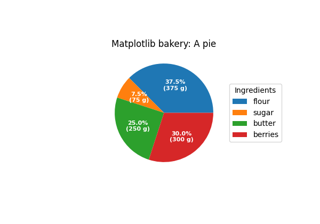
Круговые диаграммы – это наглядный способ показать доли компонент в наборе. Они идеально подходят для отчетов, презентаций и т.п. Для построения круговых диаграмм в Matplotlib используется функция pie() .
Пример построения диаграммы:
vals = [24, 17, 53, 21, 35] labels = ["Ford", "Toyota", "BMV", "AUDI", "Jaguar"] fig, ax = plt.subplots() ax.pie(vals, labels=labels) ax.axis("equal")Рассмотрим параметры функции pie() :
- x: массив
- Массив с размерами долей.
- Если параметр не равен None , то часть долей, который перечислены в передаваемом значении будут вынесены из диаграммы на заданное расстояние, пример диаграммы:
- labels: list, optional , значение по умолчанию: None
- Текстовые метки долей.
- Цвета долей.
- Формат текстовой метки внутри доли, текст – это численное значение показателя, связанного с конкретной долей.
- Расстояние между центром каждой доли и началом текстовой метки, которая определяется параметром autopct .
- Отображение тени для диаграммы.
- Расстояние, на котором будут отображены текстовые метки долей. Если параметр равен None , то метки не будет отображены.
- Задает угол, на который нужно повернуть диаграмму против часовой стрелке относительно оси x .
- Величина радиуса диаграммы.
- Определяет направление вращения – по часовой или против часовой стрелки.
- Словарь параметров, определяющих внешний вид долей.
- Словарь параметров определяющих внешний вид текстовых меток.
- Центр диаграммы.
- Если параметр равен True , то вокруг диаграммы будет отображена рамка.
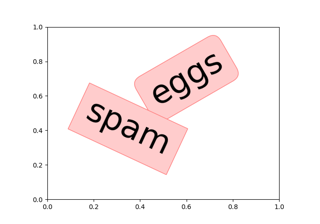
- Если параметр равен True , то текстовые метки будут повернуты на угол.
Создадим пример, в котором продемонстрируем работу с параметрами функции pie() :
vals = [24, 17, 53, 21, 35] labels = ["Ford", "Toyota", "BMV", "AUDI", "Jaguar"] explode = (0.1, 0, 0.15, 0, 0) fig, ax = plt.subplots() ax.pie(vals, labels=labels, autopct='%1.1f%%', shadow=True, explode=explode, wedgeprops=, rotatelabels=True) ax.axis("equal")Вложенные круговые диаграммы
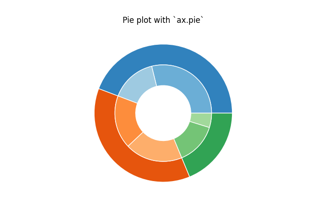
Рассмотрим пример построения вложенной круговой диаграммы. Такая диаграмма состоит из двух компонент: внутренняя ее часть является детальным представлением информации, а внешняя – суммарную по заданным областям. Каждая область представляет собой список численных значений, вместе они образуют общий набор данных. Рассмотрим на примере:
fig, ax = plt.subplots() offset=0.4 data = np.array([[5, 10, 7], [8, 15, 5], [11, 9, 7]]) cmap = plt.get_cmap("tab20b") b_colors = cmap(np.array([0, 8, 12])) sm_colors = cmap(np.array([1, 2, 3, 9, 10, 11, 13, 14, 15])) ax.pie(data.sum(axis=1), radius=1, colors=b_colors, wedgeprops=dict(width=offset, edgecolor='w')) ax.pie(data.flatten(), radius=1-offset, colors=sm_colors, wedgeprops=dict(width=offset, edgecolor='w'))Круговая диаграмма в виде бублика
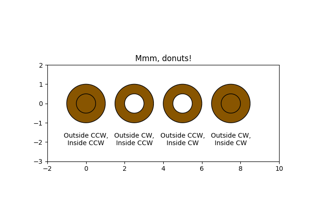
Построим круговую диаграмму в виде бублика (с отверстием посередине). Это можно сделать через параметр wedgeprops , который отвечает за внешний вид долей:
vals = [24, 17, 53, 21, 35] labels = ["Ford", "Toyota", "BMV", "AUDI", "Jaguar"] fig, ax = plt.subplots() ax.pie(vals, labels=labels, wedgeprops=dict(width=0.5))
P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Examples#
This page contains example plots. Click on any image to see the full image and source code.
For longer tutorials, see our tutorials page . You can also find external resources and a FAQ in our user guide .
Lines, bars and markers#
Images, contours and fields#
Subplots, axes and figures#
Statistics#
Pie and polar charts#
Text, labels and annotations#
The pyplot module#
Color#
For more in-depth information about the colormaps available in matplotlib as well as a description of their properties, see the colormaps tutorial .
Shapes and collections#
Style sheets#
The axes_grid1 module#
The axisartist module#
Showcase#
Animation#
Event handling#
Matplotlib supports event handling with a GUI neutral event model, so you can connect to Matplotlib events without knowledge of what user interface Matplotlib will ultimately be plugged in to. This has two advantages: the code you write will be more portable, and Matplotlib events are aware of things like data coordinate space and which axes the event occurs in so you don’t have to mess with low level transformation details to go from canvas space to data space. Object picking examples are also included.