Python list operations complexity

Time Complexities Of Python Data Structures

Every data structure performs various operations when implementing an algorithm. Some of the key and general operations include iterating over a collection, inserting an item at a point in the collection, deleting, updating or creating a copy of an item or the entire collection. In programming, the choice of the data structure is very important as it affects the performance of the application. This is because the operations of the data structures have different time and space complexities.

Space Complexity

Space Complexity is generally used to refer to the measure of how much space an algorithm takes. It includes both auxiliary space and space used by input.
Auxiliary Space is the extra space or temporary space used by an algorithm.
Space Complexity of an algorithm is total space taken by the algorithm with respect to the input size.

Time Complexity

Time Complexity is the the measure of how long it takes for the algorithm to compute the required operation. Time complexity is measured using the Big-O notation.
Big-O notation is a way to measure performance of an operation based on the input size,n.

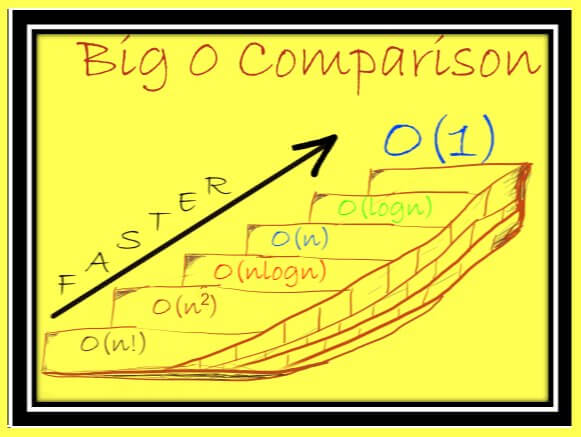
Run-time Complexity Types (BIG-O Notation Types)

1. Constant time O(1)
   An algorithm is said to have a constant time when it’s run-time not dependent on the input data(n). No matter how big your collection is, the time it takes to perform an operation is constant. This means that the algorithm/operation will always take the same amount of time regardless of the number of elements we’re working with. For example, accessing the first element of a list is always O(1) regardless of how big the list is.
2. Logarithmic time O(log n)
   Algorithms with logarithmic time complexity reduce the input data size in each step of the operation. Usually, Binary trees and Binary search operations have O(log n ) as their time complexity.
3. Linear time O(n)
   An algorithm is said to have a linear time complexity when the run-time is directly and linearly proportional to the size of the input data. This is the best possible time complexity when the algorithm has to examine all the items in the input data. For example:

for value in data: print(value) 

Example of such operations would be linear search hence the iteration over the list is O(n).

1. Quasilinear time(n log n)
   Where each operation in the input data have a logarithm time complexity. Commonly seen in optimized sorting algorithms such as mergesort, timsort, heapsort.
   In mergesort, the input data is broken down into several sub-lists until each sublist consitsts of a single element and then the sublists are merged into a sorted list. This gives us a time complexity of O(nlogn)
2. Quadratic time O(n^2):
   An algorithm is said to have a quadratic time complexity when the time it takes to perform an operation is proportional to the square of the items in the collection. This occurs when the algorithm needs to perform a linear time operation for each item in the input data. Bubble sort has O(n^2) .For example, a loop within a loop:

for x in data: for y in data: print(x, y) 

1. Exponential time O(2^n)
   An algorithm is said to have an exponential time complexity when the growth doubles with each addition to the input data set. This kind of time complexity is usually seen in brute-force algorithms. For example, the recursive Fibonacci algorithm has O(2^n) time complexity.
2. Factorial time (n!)
   An algorithm is said to have a factorial time complexity when every single permutation of a collection is computed in an operation and hence the time it takes to perform an operation is factorial of the size of the items in the collection. The Travelling Salesman Problem and the Heap’s algorithm(generating all possible permutations of n objects) have O(n!) time complexity.
   Disadvantage:It is very slow.

Big-O notation Summary Graph

Best, Average and Worst Cases

1. Best case scenario
   In the best-case analysis, we calculate lower bound on running time of an algorithm. Best-case scenario occurs when the data structures and the items in the collection along with the parameters are at their optimum state . This causes the minimum number of operations to be executed. For example, in linear search problem, the best case occurs when x(the item we are searching for) is present at the beginning of the list. The number of operations in the best case is constant (not dependent on n). So time complexity in the best case would be O(1)
2. Average case scenario
   Occurs when we define the complexity based on the uniform distribution of the values of the input.
   In average case analysis, we take all possible inputs and calculate computing time for all of the inputs. Sum all the calculated values and divide the sum by total number of inputs. We must know (or predict) distribution of cases. For the linear search problem, let us assume that all cases are uniformly distributed (including the case of x not being present in array). So we sum all the cases and divide the sum by (n+1).
3. Worst Case Scenario
   Worst case scenario could be an operation that requires finding an item that is positioned as the last item in a large-sized collection such as a list and the algorithm iterates over the collection from the very first item. For example, a linear search’s worst case occurs when x is not present in the list so the iteration compares x with all the elements.This would give us a run-time of O(n)

Time Complexities of Python Data structures

1. List
   Insert: O(n)
   Get Item: O(1)
   Delete Item:O(n)
   Iteration: O(n)
   Get Length: O(1)
2. Dictionary
   Get Item: O(1)
   Set Item: O(1)
   Delete Item: O(1)
   Iterate Over Dictionary: O(n
3. Set
   Check for item in set: O(1)
   Difference of set A from B: O(length of A)
   Intersection of set A and B: O(minimum of the length of either A or B)
   Union of set A and B: O(N) with respect to length(A) + length(B)
4. Tuples
   Tuples support all operations that do not mutate the data structure (and they
   have the same complexity classes).

Источник

Сколько стоят операции над list, set и dict в Python? Разбираемся с временной сложностью

Программисту, работающему с данными, крайне важно выбирать правильные структуры данных для решения поставленной задачи, ведь выбор неправильного типа данных плохо влияет на производительность приложения. В этой статье объясняется нотация «О» большое и сложность ключевых операций структур данных в CPython.

Что означает нотация «O» большое?

В алгоритме выполняется ряд операций. Эти операции могут включать в себя итерацию по коллекции, копирование элемента или всей коллекции, добавление элемента в коллекцию, вставку элемента в начало или конец коллекции, удаление элемента или обновление элемента в коллекции.

«O» большое служит обозначением временной сложности операций алгоритма. Она показывает, сколько времени потребуется алгоритму для вычисления требуемой операции. Можно также измерить пространственную сложность (сколько места занимает алгоритм), но в этой статье мы сосредоточимся на временной.

Проще говоря, нотация «O» большое — это способ измерения производительности операции на основе размера ввода, известного как n.

Значения нотации «О» большое

На письме временная сложность алгоритма обозначается как O(n), где n — размер входной коллекции.

O(1)

Обозначение константной временной сложности. Независимо от размера коллекции, время, необходимое для выполнения операции, константно. Это обозначение константной временной сложности. Эти операции выполняются настолько быстро, насколько возможно. Например, операции, которые проверяют, есть ли внутри коллекции элементы, имеют сложность O(1).

O(log n)

Обозначение логарифмической временной сложности. В этом случае когда размер коллекции увеличивается, время, необходимое для выполнения операции, логарифмически увеличивается. Эту сложность имеют потенциально оптимизированные алгоритмы поиска.

O(n)

Обозначение линейной временной сложности. Время, необходимое для выполнения операции, прямо и линейно пропорционально количеству элементов в коллекции. Это обозначение линейной временной сложности. Это что-то среднее с точки зрения производительности. Например, если мы хотим суммировать все элементы в коллекции, нужно будет выполнить итерацию по коллекции. Следовательно, итерация коллекции является операцией O(n).

O(n log n)

Обозначение квазилинейной временной сложности. Скорость выполнения операции является квазилинейной функцией числа элементов в коллекции. Временная сложность оптимизированного алгоритма сортировки обычно равна O(n log n).

O(n^2)

Обозначение квадратичной временной сложности. Время, необходимое для выполнения операции, пропорционально квадрату элементов в коллекции.

O(n!)

Обозначение факториальной временной сложности. Каждая операция требует вычисления всех перестановок коллекции, следовательно требуемое время выполнения операции является факториалом размера входной коллекции. Это очень медленно.

Нотация «O» большое относительна. Она не зависит от машины, игнорирует константы и понятна широкой аудитории, включая математиков, технологов, специалистов по данным и т. д.

Благоприятные, средние и худшие случаи

При вычислении временной сложности операции можно получить сложность на основе благоприятного, среднего или худшего случая.

Благоприятный случай. Как следует из названия, это сценарий, когда структуры данных и элементы в коллекции вместе с параметрами находятся в оптимальном состоянии. Например, мы хотим найти элемент в коллекции. Если этот элемент оказывается первым элементом коллекции, то это лучший сценарий для операции.

Средний случай. Определяем сложность на основе распределения значений входных данных.

Худший случай. Структуры данных и элементы в коллекции вместе с параметрами находятся в наиболее неоптимальном состоянии. Например, худший случай для операции, которой требуется найти элемент в большой коллекции в виде списка — когда искомый элемент находится в самом конце, а алгоритм перебирает коллекцию с самого начала.

Коллекции Python и их временная сложность

Список (list)

Список является одной из самых важных структур данных в Python. Можно использовать списки для создания стека или очереди. Списки — это упорядоченные и изменяемые коллекции, которые можно обновлять по желанию.

Операции списка и их временная сложность

Вставка: O(n).
Получение элемента: O(1).
Удаление элемента: O(n).
Проход: O(n).
Получение длины: O(1).

Множество (set)

Множества также являются одними из наиболее используемых типов данных в Python. Множество представляет собой неупорядоченную коллекцию. Множество не допускает дублирования, и, следовательно, каждый элемент в множестве уникален. Множество поддерживает множество математических операций, таких как объединение, разность, пересечение и так далее.

Операции с множествами и их временная сложность

Проверить наличие элемента в множестве: O(1).
Отличие множества A от B: O(длина A).
Пересечение множеств A и B: O(минимальная длина A или B).
Объединение множеств A и B: O(N) , где N это длина (A) + длина (B).

Словарь (dict)

Словарь — это коллекция пар ключ-значение. Ключи в словаре уникальны, чтобы предотвратить коллизию элементов. Это чрезвычайно полезная структура данных.

Tech Lead/Senior Python developer на продукт Data Quality (DataOps Platform) МТС , Москва, можно удалённо , По итогам собеседования

Словари индексируются по ключам, которые могут быть строками, числами или даже кортежами со строками, числами или кортежами. Над словарём можно выполнить ряд операций, таких как сохранение значения для ключа, извлечение элемента на основе ключа, или итерация по элементам и так далее.

Операции со словарями и их временная сложность

Здесь мы считаем, что ключ используется для получения, установки или удаления элемента.

Получение элемента: O(1).
Установка элемента: O(1).
Удаление элемента: O(1).
Проход по словарю: O(n).

Источник