Python генетический алгоритм функция

Генетический алгоритм на Python для поиска глобальных экстремумов

Недавно в рамках учебной деятельности мне понадобилось использовать старый добрый генетический алгоритм в целях поиска минимума и максимума функции от двух переменных. Однако, к моему удивлению, на просторах интернета не нашлось подобной реализации на питоне, а в википедии в статье по генетическому алгоритму именно этот раздел не освещен.

И поэтому я решил написать свой небольшой пакет на Python с наглядной визуализацией алгоритма, по которой будет удобно настраивать этот алгоритм и искать тонкости выбранной модели.

В этой небольшой статье я хотел бы поделиться процессом, наблюдениями и итогами.

Принцип работы алгоритма

Я не стану рассказывать о глобальном принципе работы генетических алгоритмов, но если вы ещё не слышали о таком, то ознакомиться с ним вы можете в википедии.

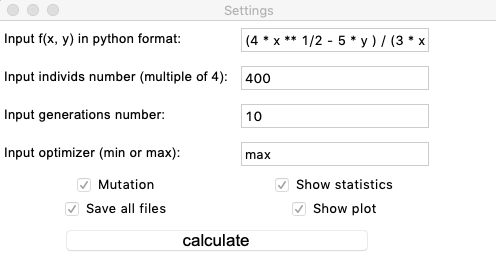
На данный момент в пакете реализован только один ГА, который параметризуется входными данными через простую гуишку. Расскажу кратко о выбранных генетических функциях и основных алгоритмических решениях.

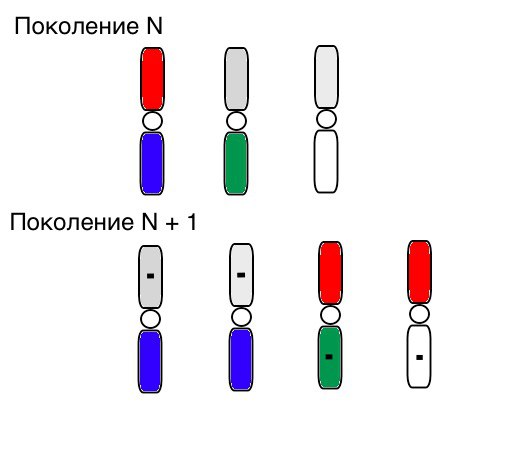
Однохромосомная особь несёт в каждом своем гене информацию о соответствующей координате х или у. Популяция определяется множеством особей, однако популяция сегментируется по 4 особи. Данное решение, конечно же, обусловлено попыткой избежать сходимость к локальному оптимуму, так как стоит задача о поиске глобального экстремума. Такое разбиение, как показала практика, во многих случаях не дает доминировать одному генотипу во всей популяции, а, наоборот, придает «эволюции» бóльшую динамику. Для каждой такой части популяции применяется следующий алгоритм:

1. Селекция происходит схоже с метод ранжирования. Выбирается 3 особи с наилучшим показателями фитнесс-функции (т.е. производится сортировка особей в порядке возрастания/убывания заданной пользователем функции, которая и выступает в роли функции приспособления).
2. Далее применяется функция скрещивания таким образом, что новое поколение (а точнее новый сегмент популяции в 4 особи) получает 2 пары немутировавших генов от особи с лучшим показанием фитнесс-функции и по паре мутировавших генов от двух других особей. Подробнее о составлении функции мутации будет написано в следующем параграфе.

Первичные тесты и наблюдения

Итак, протестируем данный алгоритм на двух простых примерах:

После тестирования и изучения работы алгоритма методом пристального взгляда и случайного тыка выявилось несколько гипотез-закономерностей:

• Погрешность алгоритма прямо пропорциональна количеству особей, но в среднем погрешность исчисляется на сотые, хотя при неудачных параметрах ошибка может достигать и десятых
• На данный момент мутация происходит прибавлением к гену рандомного числа из полуинтервала из-за чего особи не могут удержаться в окрестности экстремума и происходит относительно сильное колебание в расстоянии между особями разных поколений. В некоторых случаях такие колебания могут оказаться полезными для выхода из локального экстремума, например, периодической функции, однако экстремумы могут находиться на большом расстоянии друг от друга (расстояние в евклидовом понимании)
• Во многих случаях точка экстремума достигается особями за 5-15 поколений, а остальные поколения бесполезно «прыгают» в окрестности этого экстремума
• Нулевое поколение заполняется случайными числами только в квадрате
  и возможны случаи, когда данный квадрат покрывает локальный экстремум, что нам не подходит

Экстремумы функции g будут находится в точках

Этот пример подтверждает и иллюстрирует все выше сказанные наблюдения.

Апгрейд генетического алгоритма

Итак, на данный момент функция мутации составлена очень примитивно: она добавляет случайные величины из полуинтервала

к мутировавшему гену. Такая инвариантность мутации иногда мешает корректной работе алгоритма, но есть эффективный способ исправить этот недочёт.

Введём новый параметр, который назовём «сила мутации» (mutation range) и который будет показывать, в каком полуинтервале мутирует ген. Сделаем так, чтобы данный коэффициент мутации был обратно пропорциональна номеру поколения. Т.е. чем больше номер поколения, тем слабее мутируют гены. Это решение позволяет настраивать стартовую область и улучшать точность вычислений при необходимости.

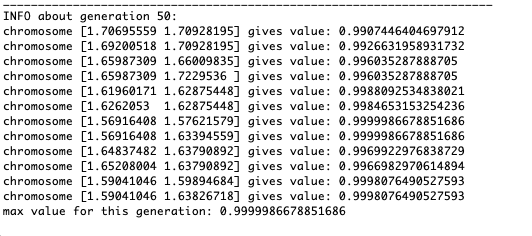
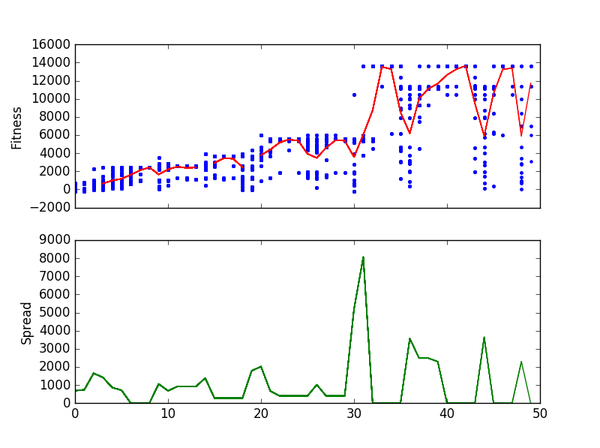
Как видно из примера, теперь, с каждым поколением популяция всё больше сходится в точку экстремума и вычисляет наиболее точные значения за счёт слабых колебаний.

А что же с проблемой локальных экстремумов? Рассмотрим уже знакомый пример.

Видим, что теперь идея с разделением популяции на части работает так, как было задумано. Без этой сегментации особи ранних поколений могли бы выявить ложный доминирующий генотип в локальном экстремуме, что привело бы к неправильному ответу в поставленной задаче. Также заметно качественное улучшение в точности ответа благодаря введенной зависимости мутации от номера поколения.

Итоги

Резюмирую полученный результат:

• Правильный набор параметров позволяет достаточно точно найти глобальный экстремум функции от двух переменных
• Разбиение популяции на части позволяет во многих случаях избежать сходимости к локальному оптимуму
• Введение силы мутации позволяет также избежать сходимости к локальному оптимуму и в разы увеличивает точность результата
• Визуализация может помочь в отладке и улучшении алгоритма, а так же помогает понимать ход и принципы самого генетического алгоритма
• повертеть графики, попроверять свои гипотезы и посмотреть код можно тут

В следующих сериях.

• Реализация других функций селекции, скрещивания и мутации. Например, интересно посмотреть, как в поставленной задаче будет работать турнирный метод селекции aka естественный отбор
• Сравнение по времени и эффективности подобных алгоритмов со стандартными методами оптимизации, например, градиентным спуском
• Новые функции пакета (вероятно)

Источник

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

License

pasaranax/GA

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

#Genetic Algorithm Генетический алгоритм, реализация на Python 3.

##Пример использования: Попробуем найти одно из решений диофантова уравнения (с целочисленными корнями): a + 2b + 3c + 4d = 30. Фитнес-функция example_diophante получает на вход список предположительных корней уравнения и возвращает отрицательное расстояние (чем больше фитнес, тем лучше) до его равенства (30). То есть при корнях являющихся решением, фитнес-функция вернет 0, во всех других случаях отрицательное число, которое чем ближе к нулю, тем больше наши корни похожи на решение.

def example_diophante(x): '''Equation: a + 2b + 3c + 4d = 30''' a, b, c, d = x z = a + 2*b + 3*c + 4*d ans = 30 print("a= b= c= d= z=".format(a, b, c, d, z), "- Solved!" if z == ans else "") return -abs(ans-z)

• steps = 40 — дадим эволюции не более 40 поколений
• stop_fitness = 0 — останавливаем эволюцию, когда функция вернула 0, значит решение найдено
• bounds = (-100, 100, 1) — предположим корни лежат где-то в диапазоне (-100, 100), шаг единица, поскольку корни целочисленные. От шага зависит точность поиска решения. Иррациональные корни ГА сможет найти с указанной точностью (0-stop_fitness).
• num_genes = 4 — у нас 4 корня
• stagnation = 3 — если эволюция войдет в застой на 3 поколения, применяем катаклизм (более сильная мутация)
• mutagen = «1_step» — у каждой особи (потенциального решения) при рождении создаем мутацию — меняем один из параметров на размер шага
• cata_mutagen = «full_step» — если мы вошли в стагнацию, применяем катаклизм — меняем все параметры на размер шага
• population_limit = 10 — в каждом поколении будем тестировать 10 вариантов решения (особей)
• survive_coef = 0.2 — из каждого поколения выбираем 20% лучших решений (то есть 2 особи из 10 смогут оставить потомков)
• productivity = 4 — на каждую из двух выживших особей после скрещивания приходится 4 потомка, то есть в новом поколении будет 8 потомков, остальные 2 места в популяции займут особи сгенерированные случайным образом
• plot = True — если установлен matplotlib, будем наблюдать эволюционный прогресс на графике

if __name__ == '__main__': ga = GA(example_equation, bounds=(-100, 100, 1), num_genes=4, steps=40, stop_fitness=0, stagnation=3, population_limit=10, survive_coef=0.2, productivity=4, mutagen="1_step", cata_mutagen="full_step", plot=True) result = ga.evolve() print("Best solution:", result)

Большинство параметров можно оставить по умолчанию, обязательны первые три.

. a=-96 b=-73 c= -4 d= 70 z= 26 a=-94 b=-71 c= -3 d= 71 z= 39 a=-94 b=-70 c= -4 d= 71 z= 38 a=-95 b=-71 c= -4 d= 70 z= 31 a=-94 b=-73 c= -4 d= 71 z= 32 a=-95 b=-73 c= -4 d= 69 z= 23 a=-94 b=-71 c= -5 d= 70 z= 29 a=-95 b=-71 c= -4 d= 71 z= 35 a=-18 b= 61 c=-100 d=-87 z=-544 a=-78 b= 74 c= 65 d= 48 z=457 - Step 9 / 40 results: best: -1.000, spread: 0.000, elapsed: 0m 1s, remaining: 0m 0s a=-94 b=-71 c= -5 d= 69 z= 25 a=-96 b=-71 c= -4 d= 70 z= 30 - Solved! a=-94 b=-70 c= -4 d= 70 z= 34 a=-94 b=-71 c= -4 d= 69 z= 28 a=-95 b=-71 c= -6 d= 70 z= 25 a=-94 b=-71 c= -6 d= 70 z= 26 a=-94 b=-71 c= -4 d= 69 z= 28 a=-95 b=-72 c= -5 d= 70 z= 26 a= 93 b=-79 c=-95 d=-26 z=-454 a=-42 b=-81 c= 30 d= 13 z=-62 - Step 10 / 40 results: best: 0.000, spread: 2.000, elapsed: 0m 1s, remaining: 0m 0s - Evolution completed: best fitness = 0.000  

Источник