Python division without remainder

Obtaining Remainder in Python Without Division: A Guide

To illustrate the issue, consider this example. In order to determine the remainder, one approach is to locate the number below N that is a multiple of D and then subtract that number from N. The remainder can then be obtained by multiplying this value by D and subtracting the result from N.

Find Quotient and Remainder of two integer without using division operators

Our objective is to determine both the quotient and remainder of two positive integers, dividend and divisor, without utilizing either the mod operator or division.

For the given input values of dividend as 10 and divisor as 3, the resulting output is 3 for the quotient and 1 for the remainder. This output demonstrates that when 10 is divided by 3, the quotient is 3 and the remainder is 1.

Given a dividend of 11 and divisor of 5, the result of the division can be represented as 2 with a remainder of 1. To clarify, this means that 5 goes into 11 twice with a remainder of 1.

To address the previously stated issue, we will employ the Binary Search approach. The search will be performed within the range of 1 through N, where N refers to the dividend. Utilizing multiplication will aid in determining this range. Upon exiting the binary search loop, the quotient will be obtained, and the remainder can be calculated using multiplication and subtraction. In instances where the dividend is less than or equal to the divisor, the special case must be handled without utilizing binary search.

Here is how the approach mentioned above has been implemented:

C++

The following list contains 101 codes: msdt_code1, msdt_code2, msdt_code3, msdt_code4, msdt_code5, msdt_code6, msdt_code7, msdt_code8, msdt_code9, msdt_code10, msdt_code11, msdt_code12, msdt_code13, msdt_code14, msdt_code15, msdt_code16, msdt_code17, msdt_code18, msdt_code19, msdt_code20, msdt_code21, msdt_code22, msdt_code23, msdt_code24, msdt_code25, msdt_code26, msdt_code27, msdt_code28, msdt_code29, msdt_code30, msdt_code31, msdt_code32, msdt_code33, msdt_code34, msdt_code35, msdt_code36, msdt_code37, msdt_code38, msdt_code39, msdt_code40, msdt_code41, msdt_code42, msdt_code43, msdt_code44, msdt_code45, msdt_code46, msdt_code47, msdt_code48, msdt_code49, msdt_code50, msdt_code51, msdt_code52, msdt_code53, msdt_code54, msdt_code55, msdt_code56, msdt_code57, msdt_code58, msdt_code59, msdt_code60, msdt_code61, msdt_code62, msdt_code63, msdt_code64, msdt_code65, msdt_code66, msdt_code67, msdt_code68, msdt_code69, msdt_code70, msdt_code71, msdt_code72, msdt_code73, msdt_code74, msdt_code75, msdt_code76, msdt_code77, msdt_code78, msdt_code79, msdt_code80, msdt_code81, msdt_code82, msdt_code83, msdt_code84, msdt_code85, msdt_code86, msdt_code87, msdt_code88, msdt_code89, msdt_code90, msdt_code91, msdt_code92, msdt_code93, msdt_code94, msdt_code95, msdt_code96, msdt_code97, msdt_code98, msdt_code99, and msdt_code100, and msdt_code101.

Java

Источник

Python division without remainder

Last updated: Feb 20, 2023
Reading time · 2 min

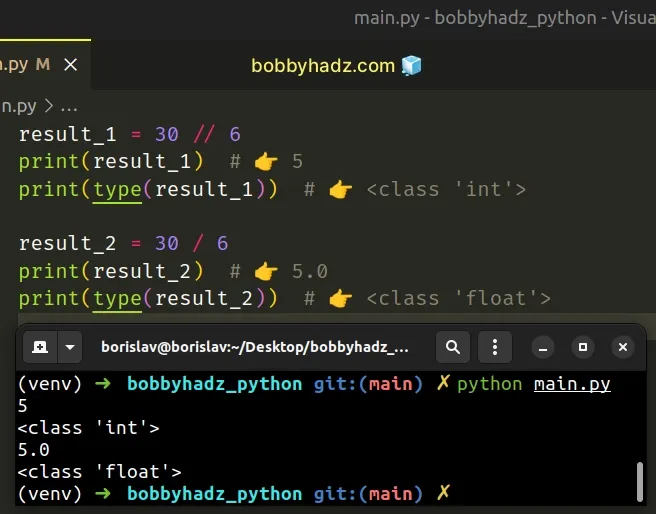
# Divide without a remainder in Python

Use the floor division operator // to divide without a remainder.

The floor division operator will always return an integer and is like using mathematical division with the floor() function applied to the result.

Copied! 
result_1 = 30 // 6 print(result_1) # 👉️ 5 print(type(result_1)) # 👉️ result_2 = 30 / 6 print(result_2) # 👉️ 5.0 print(type(result_2)) # 👉️ 

We used the floor division // operator to return an integer from integer division.

The result of using the floor division operator is that of a mathematical division with the floor() function applied to the result.

Copied! 
print(11 // 2) # 👉️ 5 print(11 / 2) # 👉️ 5.5 

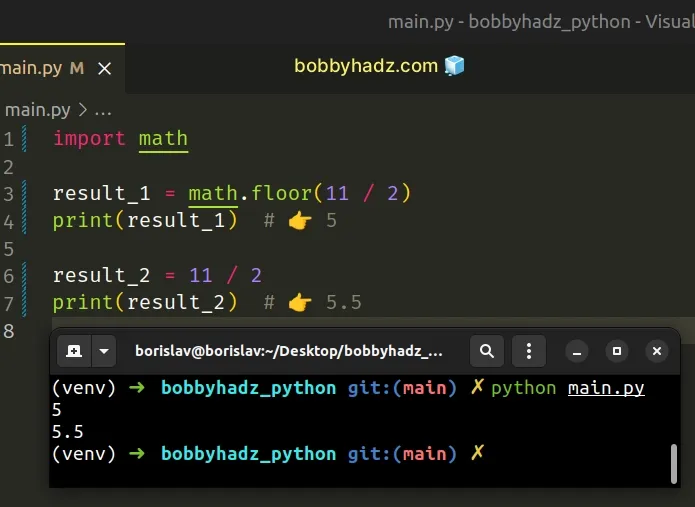
# Using math.floor()

You can use the math.floor() method in a similar way to how we used the floor division // operator.

Copied! 
import math result_1 = math.floor(11 / 2) print(result_1) # 👉️ 5 result_2 = 11 / 2 print(result_2) # 👉️ 5.5 

The math.floor method returns the largest integer less than or equal to the provided number.

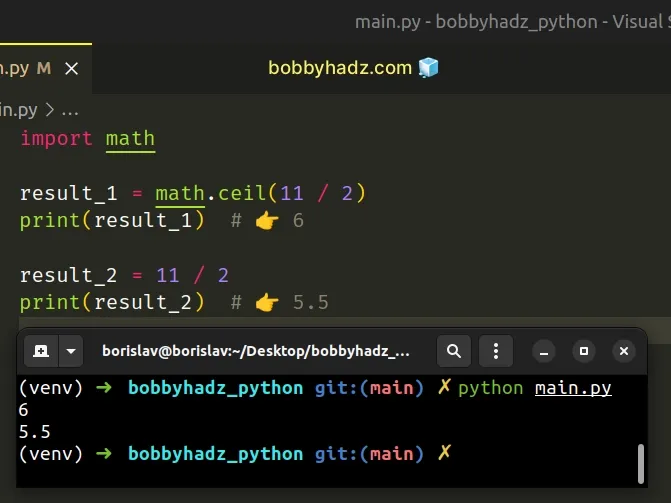
# Using math.ceil()

There is also a math.ceil() method.

Copied! 
import math result_1 = math.ceil(11 / 2) print(result_1) # 👉️ 6 result_2 = 11 / 2 print(result_2) # 👉️ 5.5 

The math.ceil method returns the smallest integer greater than or equal to the provided number.

# Using round()

You can also use the round() function if you want to round to the nearest integer when dividing.

Copied! 
result_1 = round(15 / 4) print(result_1) # 👉️ 4 result_2 = 15 / 4 print(result_2) # 👉️ 3.75 

The round function takes the following 2 parameters:

Name	Description
number	the number to round to ndigits precision after the decimal
ndigits	the number of digits after the decimal, the number should have after the operation (optional)

The round function returns the number rounded to ndigits precision after the decimal point.

If ndigits is omitted, the function returns the nearest integer.

# Divide without a remainder using int()

You can also use the int() class to remove the division decimal.

The int() class truncates floating-point numbers toward zero, so it will return an int that represents the number without the decimal places.

Copied! 
result_1 = int(7 / 2) print(result_1) # 👉️ 3 result_2 = int(-7 / 2) print(result_2) # 👉️ -3 

We used the int() class to remove the division decimal.

The int class returns an integer object constructed from the provided number or string argument.

This approach allows us to remove the division decimal from a negative number and get a predictable result.

Copied! 
result_2 = int(-7 / 2) # 👉️ = -3.5 print(result_2) # 👉️ -3 

# Divide without a remainder using math.trunc()

Alternatively, you can use the math.trunc() method.

The math.trunc() method removes the fractional part and returns the integer part of the given number.

Copied! 
import math result_1 = math.trunc(7 / 2) print(result_1) # 👉️ 3 result_2 = math.trunc(-7 / 2) print(result_2) # 👉️ -3 

The math.trunc method takes a number, removes its fractional part and returns its integer part.

The math.trunc() method rounds towards zero.

Copied! 
print(math.trunc(3.45)) # 👉️ 3 print(math.trunc(-3.45)) # 👉️ -3 

This approach achieves the same result as passing the result from the division to the int() class.

# Additional Resources

You can learn more about the related topics by checking out the following tutorials:

I wrote a book in which I share everything I know about how to become a better, more efficient programmer.

Источник

Python code to find numbers with no remainder

To execute it according to your preference, if there is no remaining value, utilize a semicolon, otherwise use a comma. To perform this in one step, use the comma operator as demonstrated in the code examples provided on codepade: first, second, third. Observe that in the if-condition, the Comma Operator is employed. To comprehend this operator, refer to the example provided.

Numbers without remainder python

It’s essential to check all three conditions in a single statement rather than dividing them into three.

for i in range(1, entered_number): if i % 2 != 0 and i % 3 != 0 and i % 5 != 0: print("The number", i, "is ok.") 

The operators at and location ensure that printing only occurs when all three requirements are fulfilled.

Your testing method evaluates each condition separately. For instance, if the number is 10 and not divisible by 3, you still print The number 10 is ok. . In contrast, for numbers that pass all tests, The number . is ok. gets printed three times since the code checks for non-divisibility by three different numbers separately.

If something divides by 7 then:

If a number is divisible by both 7 and 9, then.

something % 7 == 0 and something % 9 == 0 

On the other hand, in case a number is divisible by either 7 or 9:

something % 7 == 0 or something % 9 == 0 

The expression provided represents a value that is not divisible by either 7 or 9.

not (something % 7 == 0 or something % 9 == 0) 

To simplify your code, you can use an if-statement with a three-bit if-expression instead of using both the else: pass bits and another if-statement.

It’s advisable to verify all three conditions simultaneously.

if i%2 != 0 and i%3 != 0 and i%5 != 0: print("The number", i, "is ok.") 

Otherwise, you would end up repeating the message multiple times for a single number.

Regarding your second inquiry, the function denoted as % is referred to as modulo , which returns the remainder of a division operation. As an illustration, 5%3 = 2 holds a value of 5 = 3*1 + 2 after undergoing the said operation. Furthermore, by verifying i%2 != 0 , you are essentially checking whether i is divisible by 2.

Program to print all the numbers divisible by 3 and 5 for a given, For this divide each number from 0 to N by both 3 and 5 and check their remainder. If remainder is 0 in both cases then simply print that

Print if remainder of division with certain number is zero

To use a conditional operator, a value of else is necessary. However, if there is no intention to print anything when the condition is false, an ordinary if statement must be used instead of a conditional expression.

To create a solitary statement, use the end argument in print() to display nothing and add the newline character to the output that you want to print.

print(str(i) + '\n' if i % 1e4 == 0 else '', end='') 

for i in range(int(1e5)): if (i%1e4==0): print(i) 

0 10000 20000 30000 40000 50000 60000 70000 80000 90000 

Python Remainder Operator, In Python, the remainder is obtained using numpy.ramainder() function in numpy. It returns the remainder of the division of two arrays and returns 0 if the

Python3 function to check if parameter is a power of 2 with a while loop and without using math function

Your code encountered an infinite loop due to a unique situation with n=0 that causes 0 % 0 == 0 .

Utilizing return n == 1 can help simplify your return statement.

def is_power_of_two(n): if n == 0: return False while n % 2 == 0: n = n / 2 return n == 1 

print(is_power_of_two(0)) # Should be False print(is_power_of_two(1)) # Should be True print(is_power_of_two(8)) # Should be True print(is_power_of_two(9)) # Should be False print(is_power_of_two(8.1)) # Should be False 

False True True False False 

def is_power_of_two(n): # Check if the number can be divided by two without a remainder # special cases: 0, because 0 % 2 = 0 # you can either use the n > 0 extra test below # if n == 0: return False # or an explicit test for zero while (n > 0) and (n % 2 == 0): n = n / 2 # If after dividing by two the number is 1, it's a power of two return n == 1 

How to check if two variables have a remainder when divided, 6 days ago · Also if rem != 0 can be written as if rem , since non-zero numbers are truthy anyway. Also your while True loop is unbroken, so it will continue

How to check if the / operator has no remainder in C？

Initially, it is required to utilize the modulo operator represented by % .

Please be aware that if you are working with float or double data types, the solution would not be feasible. Instead, you should opt for fmod (double numer, double denom); .

Furthermore, to execute it according to your preference.

1. In case there is no remainder, execute x = x — 1 after if (x = 16 / 4) .
2. After executing If (x = 16 / 5) , the next step is to perform x = x + 1 .

By utilizing the comma operator expressed in , , accomplishing the task can be done in a solitary step as per the accompanying comments.

To review the functional codes, visit codepade and look for the first, second, and third ones. It is important to note that the if-condition employs the Comma Operator, which can be understood by referring to , and reading about the comma operator, along with an illustration in , .

Employ the modulus operator to compute the remainder of a division.

if (number % divisor == 0) < //code for perfect divisor >else < //the number doesn't divide perfectly by divisor >

To calculate the remainder of a division involving integers, you can utilize the modulus operator ( % ).

Function that finds how many times n can be divided in half, your loop condition isn’t correct, as repeated division will never reduce a value below zero. Given the example data, your terminating condition

Источник