Python cosine similarity matrix

Cosine Similarity – Text Similarity Metric

Text Similarity has to determine how the two text documents close to each other in terms of their context or meaning. There are various text similarity metric exist such as Cosine similarity, Euclidean distance and Jaccard Similarity. All these metrics have their own specification to measure the similarity between two queries.

In this tutorial, you will discover the Cosine similarity metric with example. You will also get to understand the mathematics behind the cosine similarity metric with example. Please refer to this tutorial to explore the Jaccard Similarity.

Cosine similarity is one of the metric to measure the text-similarity between two documents irrespective of their size in Natural language Processing. A word is represented into a vector form. The text documents are represented in n-dimensional vector space.

Mathematically, Cosine similarity metric measures the cosine of the angle between two n-dimensional vectors projected in a multi-dimensional space. The Cosine similarity of two documents will range from 0 to 1. If the Cosine similarity score is 1, it means two vectors have the same orientation. The value closer to 0 indicates that the two documents have less similarity.

The mathematical equation of Cosine similarity between two non-zero vectors is:

Let’s see the example of how to calculate the cosine similarity between two text document.

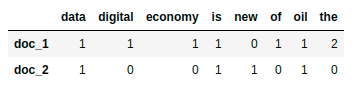
doc_1 = "Data is the oil of the digital economy" doc_2 = "Data is a new oil" # Vector representation of the document doc_1_vector = [1, 1, 1, 1, 0, 1, 1, 2] doc_2_vector = [1, 0, 0, 1, 1, 0, 1, 0] 

The Cosine Similarity is a better metric than Euclidean distance because if the two text document far apart by Euclidean distance, there are still chances that they are close to each other in terms of their context.

Compute Cosine Similarity in Python

Let’s compute the Cosine similarity between two text document and observe how it works.

The common way to compute the Cosine similarity is to first we need to count the word occurrence in each document. To count the word occurrence in each document, we can use CountVectorizer or TfidfVectorizer functions that are provided by Scikit-Learn library.

TfidfVectorizer is more powerful than CountVectorizer because of TF-IDF penalized the most occur word in the document and give less importance to those words.

Define the Data

Let’s define the sample text documents and apply CountVectorizer on it.

doc_1 = "Data is the oil of the digital economy" doc_2 = "Data is a new oil" data = [doc_1, doc_2]

Call CountVectorizer

from sklearn.feature_extraction.text import CountVectorizer count_vectorizer = CountVectorizer() vector_matrix = count_vectorizer.fit_transform(data) vector_matrix

' with 11 stored elements in Compressed Sparse Row format>

The generated vector matrix is a sparse matrix, that is not printed here. Let’s convert it to numpy array and display it with the token word.

Here, is the unique tokens list found in the data.

tokens = count_vectorizer.get_feature_names() tokens

['data', 'digital', 'economy', 'is', 'new', 'of', 'oil', 'the']

Convert sparse vector matrix to numpy array to visualize the vectorized data of doc_1 and doc_2.

array([[1, 1, 1, 1, 0, 1, 1, 2], [1, 0, 0, 1, 1, 0, 1, 0]])

Let’s create the pandas DataFrame to make a clear visualization of vectorize data along with tokens.

import pandas as pd def create_dataframe(matrix, tokens): doc_names = [f'doc_' for i, _ in enumerate(matrix)] df = pd.DataFrame(data=matrix, index=doc_names, columns=tokens) return(df)

create_dataframe(vector_matrix.toarray(),tokens)

data digital economy is new of oil the doc_1 1 1 1 1 0 1 1 2 doc_2 1 0 0 1 1 0 1 0

Find Cosine Similarity

Scikit-Learn provides the function to calculate the Cosine similarity. Let’s compute the Cosine Similarity between doc_1 and doc_2.

from sklearn.metrics.pairwise import cosine_similarity cosine_similarity_matrix = cosine_similarity(vector_matrix) create_dataframe(cosine_similarity_matrix,['doc_1','doc_2'])

doc_1 doc_2 doc_1 1.000000 0.474342 doc_2 0.474342 1.000000

By observing the above table, we can say that the Cosine Similarity between doc_1 and doc_2 is 0.47

Let’s check the cosine similarity with TfidfVectorizer, and see how it change over CountVectorizer.

Call TfidfVectorizer

from sklearn.feature_extraction.text import TfidfVectorizer Tfidf_vect = TfidfVectorizer() vector_matrix = Tfidf_vect.fit_transform(data) tokens = Tfidf_vect.get_feature_names() create_dataframe(vector_matrix.toarray(),tokens)

data digital economy is new of oil the doc_1 0.243777 0.34262 0.34262 0.243777 0.000000 0.34262 0.243777 0.68524 doc_2 0.448321 0.00000 0.00000 0.448321 0.630099 0.00000 0.448321 0.00000

cosine_similarity_matrix = cosine_similarity(vector_matrix) create_dataframe(cosine_similarity_matrix,['doc_1','doc_2'])

doc_1 doc_2 doc_1 1.000000 0.327871 doc_2 0.327871 1.000000

Here, using TfidfVectorizer we get the cosine similarity between doc_1 and doc_2 is 0.32. Where the CountVectorizer has returned the cosine similarity of doc_1 and doc_2 is 0.47. TfidfVectorizer penalized the most frequent words in the document such as stopwords.

In this tutorial, you learn about cosine similarity and how to find it with example in Python. Please refer to this tutorial to explore the other text similarity metric Jaccard Similarity.

Источник

How to Create Similarity Matrix in Python (Cosine, Pearson)

Cosine similarity measures the cosine of the angle between two non-zero vectors in a high-dimensional space. It is often used in natural language processing to compare documents or words based on their term frequency or Term frequency–inverse document frequency (TF-IDF) values.

TF-IDF, is a numerical statistic that is intended to reflect how important a word is to a document in a collection or corpus.

To build cosine similarity matrix in Python we can use:

• collect a list of documents
• create a TfidfVectorizer object
• compute the document-term matrix
• compute the cosine similarity matrix

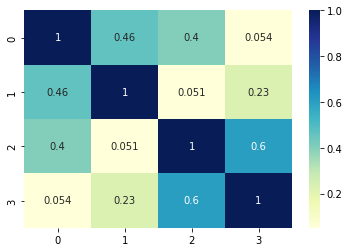
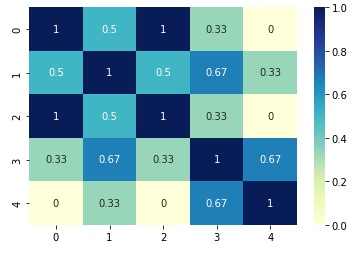
from sklearn.metrics.pairwise import cosine_similarity from sklearn.feature_extraction.text import TfidfVectorizer documents = [ "The quick brown fox jumps over the lazy dog", "A quick brown dog outpaces a quick fox", "The slow grey cat watches the fast dog", "A slow grey dog outpaces a fast cat", ] vectorizer = TfidfVectorizer() doc_term_matrix = vectorizer.fit_transform(documents) cosine_sim_matrix = cosine_similarity(doc_term_matrix) print(cosine_sim_matrix) 

The resulted cosine similarity matrix is shown below:

[[1. 0.46466784 0.39981419 0.05364441] [0.46466784 1. 0.05067865 0.22611742] [0.39981419 0.05067865 1. 0.60042396] [0.05364441 0.22611742 0.60042396 1. ]] 

Visualize similarity matrix

We can visualize the similarity matrix by using seaborn library:

import seaborn as sns import matplotlib.pyplot as plt sns.heatmap(cosine_sim_matrix, annot=True, cmap="YlGnBu") plt.show() 

Euclidean distances

To compute euclidean distances of several numerical vectors we can use numpy.

The example below shows how to create similarity matrix based on euclidean distances:

import numpy as np vectors = np.array([ [3, 4, 6, 1, 3, 4], [7, 5 ,3, 1, 3, 6], [2, 7, 4, 8, 9, 6], [3, 5, 6, 8, 7, 9] ]) euclidean_distances = np.sqrt(((vectors[:, np.newaxis] - vectors) ** 2).sum(axis=2)) print(euclidean_distances) 

[[ 0. 5.47722558 10.14889157 9.53939201] [ 5.47722558 0. 10.72380529 9.94987437] [10.14889157 10.72380529 0. 4.69041576] [ 9.53939201 9.94987437 4.69041576 0. ]] 

Difflib

We can build a custom similarity matrix using for and library difflib. We will use method: .SequenceMatcher(None,n,m).ratio() — to compute similarity between two numerical vectors in Python:

• loop over each list of numbers
• then loop the rest
• calculate the similarity of both lists
• store the similarity ratio

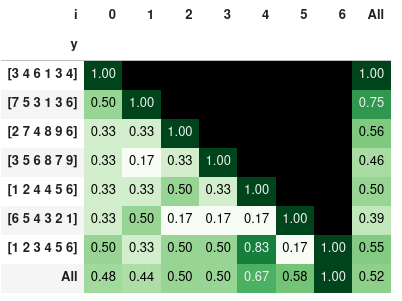
import difflib vectors = np.array([ [3, 4, 6, 1, 3, 4], [7, 5 ,3, 1, 3, 6], [2, 7, 4, 8, 9, 6], [3, 5, 6, 8, 7, 9], [1, 2, 4, 4, 5, 6], [6, 5, 4, 3, 2, 1], [1, 2, 3, 4, 5, 6,] ]) s = [] for i, n in enumerate(vectors): for m in vectors[i:]: r = difflib.SequenceMatcher(None,n,m).ratio() s.append() df_p = pd.DataFrame(s) df_p[['x', 'y']] = df_p[['x', 'y']].astype(str) df_p 

x	y	r	i
0	[3 4 6 1 3 4]	[3 4 6 1 3 4]	1.000000	0
1	[3 4 6 1 3 4]	[7 5 3 1 3 6]	0.500000	0
2	[3 4 6 1 3 4]	[2 7 4 8 9 6]	0.333333	0
3	[3 4 6 1 3 4]	[3 5 6 8 7 9]	0.333333	0
4	[3 4 6 1 3 4]	[1 2 4 4 5 6]	0.333333	0

Now we can visualize the similarity ratio in matrix form by using Pandas pivot table and styling:

pd.pivot_table(df_p, index='y', columns='i', values='r', sort=False, margins=True)\ .style.background_gradient(cmap='Greens',axis=None).format(na_rep='', precision=2) 

the similarity ratio styled with colors:

Note: the last 3 examples show that order is important. So you may sort the lists prior comparison — in case that you would like to compare only the elements and not the order.

Pearson correlation matrix

We can use Pandas library to calculate Pearson correlation coefficients in Python. We will use method: df.corr(method=’pearson’) :

import pandas as pd data = df = pd.DataFrame(data) corr_matrix = df.corr(method='pearson') sns.heatmap(corr_matrix, annot=True, cmap="YlGnBu") plt.show() 

we can display the matrix with seaborn again:

To understand the results consider:

• coefficients range between -1 and 1
• -1 indicates a perfect negative linear correlation
• 0 indicates no linear correlation
• 1 indicates a perfect positive linear correlation

Jaccard similarity matrix

For Jaccard similarity we will use only binary values. The example below use library sklearn to calculate Jaccard score:

from sklearn.metrics import jaccard_score data = [[0, 1, 0], [0, 1, 1], [0, 1, 0], [1, 1, 1], [1, 0, 1]] similarity_matrix = [] for i in range(len(data)): row = [] for j in range(len(data)): row.append(jaccard_score(data[i], data[j])) similarity_matrix.append(row) sns.heatmap(pd.DataFrame(similarity_matrix), annot=True, cmap="YlGnBu") plt.show() 

The result is shown below:

Inter element similarity

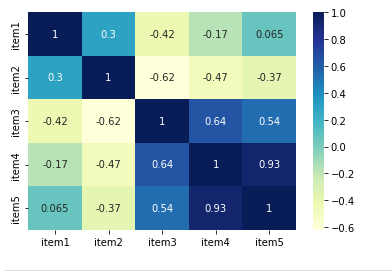
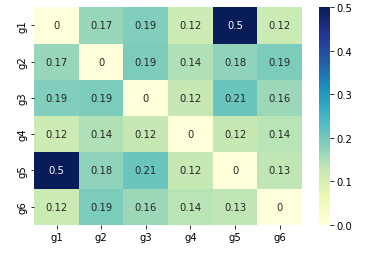
We can also check the similarity, correlation or distance between elements of arrays. We will show one example using scipy.

In this example we are comparing six variables: [«g1″,»g2″,»g3″,»g4″,»g5», «g6»]

import pandas as pd from scipy.spatial.distance import euclidean, pdist, squareform def similarity_func(u, v): return 1/(1+euclidean(u,v)) DF_var = pd.DataFrame.from_dict(<"s1":[3, 4, 6, 1, 3, 4],"s2":[3, 5 ,3, 1, 3, 6],"s3":[3, 7, 4, 8, 3, 6],"s4":[3, 5, 6, 8, 4, 9]>) DF_var.index = ["g1","g2","g3","g4","g5", "g6"] dists = pdist(DF_var, similarity_func) DF_euclid = pd.DataFrame(squareform(dists), columns=DF_var.index, index=DF_var.index) sns.heatmap(DF_euclid, annot=True, cmap="YlGnBu") plt.show() 

So we have strongest relatation between g1 and g5:

Resources

Источник