Python check if point in polygon

Point in Polygon in Python

About the algorithm and language used in this code snippet:

Point in Polygon Algorithm

The Point in Polygon (PIP) problem is the problem of determining whether a point is any arbitrary polygon. This might sound trivial for a simple polygon like a square or a triangle, but gets more complex with more complex polygons like the one in the example below. In this post, the even-odd algorithm, also called crossing number algorithm or Jordan’s algorithm (since it can be proven using the Jordan curve theorem), will be introduced.

Description of the Algorithm

The basic principle behind the Even-odd aka. Jordan aka. Cross Number Algorithm is to count the number of times a line from the point in question (in any, arbitrary direction) crosses any edge of the polygon. This line will always be outside of the polygon at it’s “end” in infinity, so if it is inside the polygon at the start (the point in question), it will have to leave the polygon at some point, crossing some edge. It can re-enter the polygon (see the example below), but it always has to leave again, making the total number of crossings uneven if the point is in the polygon. The opposite is also true; if the number of crossings is even, the point is always outside of the polygon. This is the above mentioned Jordan’s curve theorem.

The algorithm checks every edge of the polygon in a loop to determine if the line from the point to infinity crosses it. In the example below, this line is drawn from the point to infinity to the right, but it can be any direction.

1. For each edge in the polygon:
2. If the edge crosses the imaginary line from the point to infinity, increase a counter.
3. At then end, if the counter is uneven, return true. Else, return false.

A simple boolean variable that is inverted every time a crossing is found is also possible.

Example of the Algorithm

Consider the following polygon with 8 edges and two points for which we want to determine whether they are in the polygon:

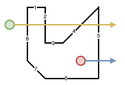
The steps the algorithm performs on this polygon to determine whether the first (green) point is in the polygon are, starting from the first edge:

1. Green Point crosses edge 8
2. Green Point does not cross edge 1
3. Green Point crosses edge 2
4. Green Point does not cross edge 3
5. Green Point crosses edge 4
6. Green Point crosses edge 5
7. Green Point does not cross edge 6
8. Green Point does not cross edge 7
9. Total number of crossings: 4
10. Even number of edge crossings, therefore the point is not in the polygon

The steps the algorithm performs on this polygon to determine whether the second (red) point is in the polygon are, starting from the first edge:

1. Red Point does not cross edge 8
2. Red Point does not cross edge 1
3. Red Point does not cross edge 2
4. Red Point does not cross edge 3
5. Red Point does not cross edge 4
6. Red Point crosses edge 5
7. Red Point does not cross edge 6
8. Red Point does not cross edge 7
9. Total number of crossings: 1
10. Uneven number of edge crossings, therefore the point is in the polygon

Runtime Complexity of the Algorithm

The runtime complexity of the Jordan Algorithm aka. Crossing Number Algorithm aka. Even-Odd Algorithm to solve the point-in-polygon problem for a single point is linear with respect to the number of edges. This is evident by looking at the code, which contains a single loop over the edges, with no recursion or further function calls or loops.

Formally the runtime is O(|V|), |V|:=number of edges in the polygon.

Space Complexity of the Algorithm

The space complexity is also linear w.r.t. the number of edges, since only fixed-size variables need to be stored in addition to the polygon. Additionally, the algorithm can be implemented on-line, meaning there is no need to look at past edges during the loop, so they can be evicted from memory (or comparable performance improvement measures).

Источник

Run Fast Point-in-Polygon Tests

Performing point-in-polygon queries is one of the most commonplace operations in geospatial analysis and GIS. As Python is a great tool for automating GIS workflows, being able to solve this basic problem of computational geometry as efficiently as possible is often a prerequisite for further analysis.

How to check if a point is inside a polygon in Python

To perform a Point in Polygon (PIP) query in Python, we can resort to the Shapely library’s functions .within(), to check if a point is within a polygon, or .contains(), to check if a polygon contains a point.

Here’s some example code on how to use Shapely.

from shapely.geometry import Point, Polygon # Create Point objects p1 = Point(24.82, 60.24) p2 = Point(24.895, 60.05) # Create a square coords = [(24.89, 60.06), (24.75, 60.06), (24.75, 60.30), (24.89, 60.30)] poly = Polygon(coords) # PIP test with 'within' p1.within(poly) # True p2.within(poly) # False # PIP test with 'contains' poly.contains(p1) # True poly.contains(p2) # False 

How to get a list of points inside a polygon in Python

One of the simplest and most efficient ways of getting a list of points inside a polygon with Python is to rely on the Geopandas library and perform a spatial join. To do this, we simply create one geodataframe with points and another one with polygons, and join them with ‘sjoin’.

In this example, we will use, as polygons, the shapefile of US counties and a list of random points, uniformly distributed in the lat-long region of (23,51)x(-126,-64).

Let’s begin by importing all the libraries we are going to need

import geopandas as gpd import pandas as pd import numpy as np import matplotlib.pyplot as plt from shapely.geometry import Point

Now we open a shapefile containing our polygons

# Open the shapefile counties = gpd.GeoDataFrame.from_file('cb_2018_us_county_20m.shp')

That’s it for the polygons, let’s move on now to generate a GeoDataFrame with some points

# Generate random points N=10000 lat = np.random.uniform(23,51,N) lon = np.random.uniform(-126,-64,N) # Create geodataframe from numpy arrays df = pd.DataFrame('lon':lon, 'lat':lat>) df['coords'] = list(zip(df['lon'],df['lat'])) df['coords'] = df['coords'].apply(Point) points = gpd.GeoDataFrame(df, geometry='coords', crs=counties.crs)

Finally, let’s perform the spatial join:

# Perform spatial join to match points and polygons pointInPolys = gpd.tools.sjoin(points, counties, predicate="within", how='left')

That’s it, we have just matched points and polygons!

Now, let’s use this to retrieve the points from a specific polygon, as follows:

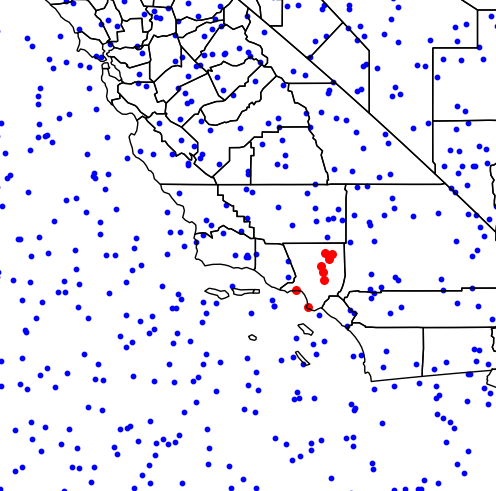
# Example use: get points in Los Angeles, CA. pnt_LA = points[pointInPolys.NAME=='Los Angeles']

That’s it, now let’s plot everything

# Plot map with points in LA in red base = counties.boundary.plot(linewidth=1, edgecolor="black") points.plot(ax=base, linewidth=1, color="blue", markersize=1) pnt_LA.plot(ax=base, linewidth=1, color="red", markersize=8) plt.show()

This will produce the following image:

You can download the complete script here

Speeding up Geopandas point-in-polygon tests

Performance issues become increasingly important as the size of the datasets under consideration grows to millions of points or thousands of polygons. For this matter, it is important to employ the most efficient algorithms and implementations at hand.

Importantly, projects like Shapely and Geopandas continue to evolve and subsequent releases include performance optimizations. Within Geopandas, an important thing to look for is to install some optional dependencies.

Use Rtree

Spatial indexing techniques such as R-trees can provide speed-ups of orders of magnitudes for queries like intersections and joins.

For example, Geopandas optionally includes the Python package Rtree as an optional dependency (see the github repo).

Be sure to install the C-library libspatialindex first, on which Rtree relies upon.

Use the optimized PyGEOS library

Another interesting development has been the Cythonised version of Geopandas, reported here. Currently, the fast Cython implementations live in the PyGEOS package, and instructions on how to build Geopandas with the optional PyGEOS dependency can be checked in the documentation. PyGEOS can significantly improve the performance of sjoin.

Final remarks

Point-in-polygon queries are one of the most commonplace operations in geospatial analysis and GIS. As shown in this small tutorial, they can be performed easily and efficiently within Python. It is important also to stay tuned with the ongoing development of the underlying libraries, and to be sure to have the last versions installed, together with all relevant dependencies!

Источник

Point in Polygon & Intersect¶

Finding out if a certain point is located inside or outside of an area, or finding out if a line intersects with another line or polygon are fundamental geospatial operations that are often used e.g. to select data based on location. Such spatial queries are one of the typical first steps of the workflow when doing spatial analysis. Performing a spatial join (will be introduced later) between two spatial datasets is one of the most typical applications where Point in Polygon (PIP) query is used.

For further reading about PIP and other geometric operations, see Chapter 4.2 in Smith, Goodchild & Longley: Geospatial Analysis — 6th edition.

How to check if point is inside a polygon?¶

Computationally, detecting if a point is inside a polygon is most commonly done using a specific formula called Ray Casting algorithm. Luckily, we do not need to create such a function ourselves for conducting the Point in Polygon (PIP) query. Instead, we can take advantage of Shapely’s binary predicates that can evaluate the topolocical relationships between geographical objects, such as the PIP as we’re interested here.

There are basically two ways of conducting PIP in Shapely:

1. using a function called .within() that checks if a point is within a polygon
2. using a function called .contains() that checks if a polygon contains a point

Notice: even though we are talking here about Point in Polygon operation, it is also possible to check if a LineString or Polygon is inside another Polygon.

from shapely.geometry import Point, Polygon # Create Point objects p1 = Point(24.952242, 60.1696017) p2 = Point(24.976567, 60.1612500) 

# Create a Polygon coords = [(24.950899, 60.169158), (24.953492, 60.169158), (24.953510, 60.170104), (24.950958, 60.169990)] poly = Polygon(coords) 

# Let's check what we have print(p1) print(p2) print(poly) 

POINT (24.952242 60.1696017) POINT (24.976567 60.16125) POLYGON ((24.950899 60.169158, 24.953492 60.169158, 24.95351 60.170104, 24.950958 60.16999, 24.950899 60.169158))

# Check if p1 is within the polygon using the within function p1.within(poly) 

Источник

Point-in-polygon queries#

Finding out if a certain point is located inside or outside of an area, or finding out if a line intersects with another line or polygon are fundamental geospatial operations that are often used e.g. to select data based on location. Such spatial queries are one of the typical first steps of the workflow when doing spatial analysis. Performing a spatial join (will be introduced later) between two spatial datasets is one of the most typical applications where Point in Polygon (PIP) query is used.

For further reading about PIP and other geometric operations, see Chapter 4.2 in Smith, Goodchild & Longley: Geospatial Analysis — 6th edition.

How to check if point is inside a polygon?#

Computationally, detecting if a point is inside a polygon is most commonly done using a specific formula called Ray Casting algorithm. Luckily, we do not need to create such a function ourselves for conducting the Point in Polygon (PIP) query. Instead, we can take advantage of Shapely’s binary predicates that can evaluate the topolocical relationships between geographical objects, such as the PIP as we’re interested here.

Point-in-polygon queries on shapely geometries#

There are basically two ways of conducting PIP in Shapely:

1. using a function called within() that checks if a point is within a polygon
2. using a function called contains() that checks if a polygon contains a point

Even though we are talking here about Point in Polygon operation, it is also possible to check if a LineString or Polygon is inside another Polygon.

Let’s first create a couple of point geometries:

import shapely.geometry point1 = shapely.geometry.Point(24.952242, 60.1696017) point2 = shapely.geometry.Point(24.976567, 60.1612500) 

polygon = shapely.geometry.Polygon( [ (24.950899, 60.169158), (24.953492, 60.169158), (24.953510, 60.170104), (24.950958, 60.169990) ] ) 

print(point1) print(point2) print(polygon) 

POINT (24.952242 60.1696017) POINT (24.976567 60.16125) POLYGON ((24.950899 60.169158, 24.953492 60.169158, 24.95351 60.170104, 24.950958 60.16999, 24.950899 60.169158))

Let’s check if the points are within() the polygon:

Источник