Python быстрое умножение матриц

numpy.matmul#

A location into which the result is stored. If provided, it must have a shape that matches the signature (n,k),(k,m)->(n,m). If not provided or None, a freshly-allocated array is returned.

For other keyword-only arguments, see the ufunc docs .

New in version 1.16: Now handles ufunc kwargs

The matrix product of the inputs. This is a scalar only when both x1, x2 are 1-d vectors.

If the last dimension of x1 is not the same size as the second-to-last dimension of x2.

If a scalar value is passed in.

Complex-conjugating dot product.

Sum products over arbitrary axes.

Einstein summation convention.

alternative matrix product with different broadcasting rules.

The behavior depends on the arguments in the following way.

• If both arguments are 2-D they are multiplied like conventional matrices.
• If either argument is N-D, N > 2, it is treated as a stack of matrices residing in the last two indexes and broadcast accordingly.
• If the first argument is 1-D, it is promoted to a matrix by prepending a 1 to its dimensions. After matrix multiplication the prepended 1 is removed.
• If the second argument is 1-D, it is promoted to a matrix by appending a 1 to its dimensions. After matrix multiplication the appended 1 is removed.

matmul differs from dot in two important ways:

• Multiplication by scalars is not allowed, use * instead.
• Stacks of matrices are broadcast together as if the matrices were elements, respecting the signature (n,k),(k,m)->(n,m) :

>>> a = np.ones([9, 5, 7, 4]) >>> c = np.ones([9, 5, 4, 3]) >>> np.dot(a, c).shape (9, 5, 7, 9, 5, 3) >>> np.matmul(a, c).shape (9, 5, 7, 3) >>> # n is 7, k is 4, m is 3 

The matmul function implements the semantics of the @ operator introduced in Python 3.5 following PEP 465.

It uses an optimized BLAS library when possible (see numpy.linalg ).

For 2-D arrays it is the matrix product:

>>> a = np.array([[1, 0], . [0, 1]]) >>> b = np.array([[4, 1], . [2, 2]]) >>> np.matmul(a, b) array([[4, 1], [2, 2]]) 

For 2-D mixed with 1-D, the result is the usual.

>>> a = np.array([[1, 0], . [0, 1]]) >>> b = np.array([1, 2]) >>> np.matmul(a, b) array([1, 2]) >>> np.matmul(b, a) array([1, 2]) 

Broadcasting is conventional for stacks of arrays

>>> a = np.arange(2 * 2 * 4).reshape((2, 2, 4)) >>> b = np.arange(2 * 2 * 4).reshape((2, 4, 2)) >>> np.matmul(a,b).shape (2, 2, 2) >>> np.matmul(a, b)[0, 1, 1] 98 >>> sum(a[0, 1, :] * b[0 , :, 1]) 98 

Vector, vector returns the scalar inner product, but neither argument is complex-conjugated:

Scalar multiplication raises an error.

>>> np.matmul([1,2], 3) Traceback (most recent call last): . ValueError: matmul: Input operand 1 does not have enough dimensions . 

The @ operator can be used as a shorthand for np.matmul on ndarrays.

>>> x1 = np.array([2j, 3j]) >>> x2 = np.array([2j, 3j]) >>> x1 @ x2 (-13+0j) 

Источник

Умножение матриц в Python без NumPy

Умножение матриц является фундаментальной операцией в линейной алгебре.

Обычно мы используем его во многих приложениях, таких как обработка изображений, машинное обучение и многие другие. NumPy — известный пакет Python для научных вычислений.

Однако в этом посте мы рассмотрим различные методы умножения матриц в Python без использования NumPy.

мы будем использовать вложенные циклы, встроенная функция map() и понимание списка.

Кроме того, мы рассмотрим преимущества и недостатки каждой стратегии, а также когда применять каждую из них. Если вы новичок в линейной алгебре и хотите узнать больше об умножении матриц; продолжайте читать.

Где мы используем умножение матриц?

Умножение матриц используется в компьютерная графика изменять 2D и 3D изображения. Например, вы можете вращать, масштабировать и перемещать объекты на экране. Матрицы используются при обработке изображений для представления изображений в виде массивов пикселей. Кроме того, матрицы могут использоваться для проведения таких операций, как фильтрация изображений.

Мы также используем матрицы в обучение с помощью машины. Они могут помочь нам представить данные и параметры модели. Мы можем выполнять множество операций, таких как вычисление скалярных произведений и матрично-векторных произведений.

Несомненно, эта операция очень выгодна и в научных операциях. Мы можем использовать его в физике и технике для описания физических величин. Следовательно, мы можем оперировать векторами и тензорами.

Почему мы не можем использовать NumPy?

В то время как NumPy является Библиотека Python, это не всегда идеальный вариант для умножения матриц. Мы можем не использовать NumPy по таким причинам, как размер и зависимость, обучение и устаревшие системы.

В некоторых случаях использование встроенных функций Python или разработка собственного кода могут оказаться более эффективными. Однако важно отметить, что NumPy — мощная библиотека. Кроме того, вы также можете использовать его для умножения матриц.

Теперь давайте посмотрим, как мы можем добиться умножения матриц без NumPy.

Метод вложенных циклов

Техника вложенных циклов использует вложенные циклы для выполнения умножения матриц в Python. Функция перебирает каждый элемент матрицы. И он умножает их, используя серию вложенных циклов. Функция возвращает результат, который сохраняется в новой матрице.

Этот подход прост для понимания. Однако он может быть не таким эффективным, как другие способы, особенно для больших матриц. Тем не менее, это прекрасный выбор для вас, если вы новичок в линейной алгебре.

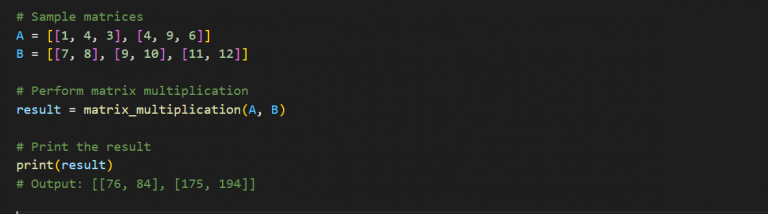
def matrix_multiplication(A, B):

# Determine the matrices’ dimensions.

# Установить матрицу результатов в нули.

result = [[0 for row in range(cols_B)] for col in

# Iterate through rows of A

# Iterate through columns of B

# Iterate through rows of B

Давайте рассмотрим пример того, как это сделать. Вы можете просто добавить эти строки кода ниже, чтобы протестировать этот пример.

# Perform matrix multiplication

result = matrix_multiplication(A, B)

Выгоды:

• Легко понять.
• Отлично подходит для новичков или тех, кто ищет более глубокое понимание матричного умножения.

Минусы:

• Не так эффективен, как альтернативные методы, особенно для больших матриц.
• Это не так читабельно, как альтернативные подходы.

Метод функции map()

Метод функции map() предоставляет альтернативный подход к умножению матриц в Python. В этом подходе мы используем встроенную функцию map(). Следовательно, мы используем инструмент функционального программирования, который применяет предоставленную функцию к каждому итерируемому элементу (списку, кортежу и т. д.). Кроме того, функция map() принимает два параметра: функцию и итерируемый объект. И он возвращает итератор, который применяет функцию к каждому итерируемому элементу.

В этом подходе мы просматриваем каждый элемент матрицы и выполняем умножение с помощью вложенной функции map().

Функция zip() используется для параллельного перебора каждого элемента матриц.

Наконец, функция sum() используется для суммирования результатов.

def matrix_multiplication(A, B):

# To get the dimensions of the matrices

# We use map() function for multiplication.

result = [[sum(a * b for a, b in zip(row_a, col_b)) for

col_b in zip(*B)] for row_a in A]

Теперь снова мы можем протестировать наш код на примере.

# Use map() function to perform matrix multiplication

result = list(map(lambda x: list(map(lambda y: sum(i*j

Преимущества

• Более эффективен, чем метод сложенных циклов
• Он использует функциональное программирование, чтобы сделать код проще.

Недостатки бонуса без депозита

• Некоторым людям, не знакомым с функциональным программированием, это может показаться менее читаемым.
• Это менее понятно, чем техника вложенных циклов.

Метод понимания списка

Понимание списков позволяет создать новый список в одной строке кода. Следовательно, это путем применения выражения к каждому члену существующего списка.

В этом подходе умножение выполняется путем многократного повторения каждого элемента матрицы. Мы используем понимание многоуровневого списка.

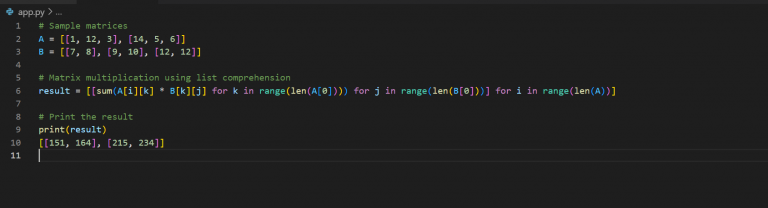
# Matrix multiplication using list comprehension

result = [[sum(A[i][k] * B[k][j] for k in range(len(A[0])))

for j in range(len(B[0]))] for i in range(len(A))]

Преимущества

Недостатки бонуса без депозита

• Это может быть менее эффективно, чем использование функции map(), особенно для больших матриц.
• Это сложнее, чем подход с вложенными циклами.

Заключение

В этом посте мы рассмотрели альтернативы использованию NumPy при умножении матриц в Python. Мы выполнили умножение матриц во вложенных циклах, встроенной функции map() и анализе списка.

Лучшая стратегия будет зависеть от конкретных потребностей вашего проекта.

Каждая из стратегий имеет свои плюсы и минусы. Чтобы убедиться, что функция работает правильно, рекомендуется добавить несколько тестовых случаев с различными размерами и значениями матрицы.

Вы также должны включить некоторые тесты производительности, чтобы сравнить, насколько хорошо эти методы работают.

Источник

Как ускорить перемножение матриц в numpy?

У меня есть 2 матрицы размером 2500*2500, заполненные с случными числами от 0 до 500. Сначала матрицы A и B разделяю на подматрицы с помощью numpy.array_slit. Потом умножаю подматрицы с помощью dot в одном потоке. Eсли так сделать, то уходит много времени.
Хочу сделать умножение подматриц в отдельных потоках. То есть например мартрицу А разделяю на две части на a1 и a2. Также B матрицу разделяю на b1 и b1. Хочу в tread1 умножить a1 и b1, в tread2 умножить a2 и b2. Как это реализовать? Какой нибудь метод есть в numpy, что отдельно умножить подматрицы?

import threading import numpy as np import timeit import time thread_lock = threading.Lock() class MyThread(threading.Thread): def __init__(self, name, delay, a, b): threading.Thread.__init__(self) self.name = name self.delay = delay self.a= a self.b = b def run(self): print('Starting thread %s.' % self.name) thread_lock.acquire() matrix_multiplctn(self.a,self.b, self.delay) thread_lock.release() print('Finished thread %s.' % self.name ) def matrix_multiplctn(a, b, delay): a1=np.array_split(a, 2, axis=1) #разделяю по столбцам b1=np.array_split(b, 2, axis=0) #разделяю по строкам start_time = timeit.default_timer() c = np.dot(a1,b1) print(timeit.default_timer() - start_time) time.sleep(delay) print(c) a=np.random.randint(0,500, size=(2500,2500)) b=np.random.randint(0,500, size=(2500,2500)) thread = MyThread("A", 0.1, a, b) start_time1 = timeit.default_timer() thread.start() thread.join() print("Время выполнения A: ", timeit.default_timer() - start_time1) print('Finished.')

Средний 1 комментарий

Источник