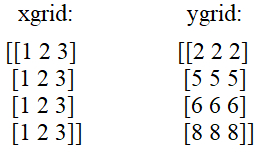Как строить трехмерные графики
Следующим шагом мы с вами рассмотрим возможности построения трехмерных графиков в пакете matplotlib. Такая возможность появилась, начиная с версии 0.99, поэтому убедитесь, что ваш пакет поддерживает трехмерные графики.
Все дополнительные классы для работы в 3D находятся в модуле:
и вначале мы его импортируем в нашу программу наряду с самим пакетом matplotlib и numpy:
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D
А, затем, создадим трехмерную систему координат:
fig = plt.figure(figsize=(7, 4)) ax_3d = Axes3D(fig) plt.show()
При выполнении этой простой программы, мы в окне увидим три пространственные оси, которые можно вращать с помощью курсора мышки:
Того же самого результат можно добиться, используя параметр projection при создании системы координат:
fig = plt.figure(figsize=(7, 4)) ax_3d = fig.add_subplot(projection='3d')
Как именно создавать трехмерные оси, зависит от вашего выбора и удобства при написании конкретных программ. Я остановлюсь на втором способе.
- plot() – линейный 2D график в трех измерениях;
- step() – ступенчатый 2D график в трех измерениях;
- scatter() – точеный график 3D график.
- plot_wireframe() – построение каркасной поверхности в 3D;
- plot_surface() – построение непрерывной 3D поверхности.
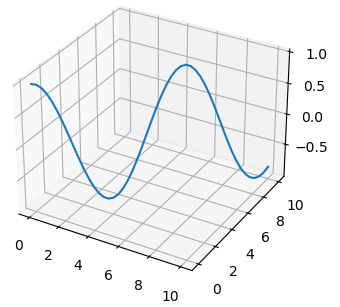
x = np.linspace(0, 10, 50) z = np.cos(x) ax_3d.plot(x, x, z)
То есть, мы здесь по координатам x, y выбираем одни и те же значения, а координата z (вертикаль) – это значение функции. Давайте подпишем оси, чтобы видеть, где какая расположена на этом графике:
ax_3d.set_xlabel('x') ax_3d.set_ylabel('y') ax_3d.set_zlabel('z')
Но то, что мы получили, это не совсем трехмерный график. Скорее, это двумерная косинусоида в трех измерениях. Давайте построим настоящее трехмерное изображение, например, вот такой функции: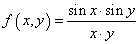 
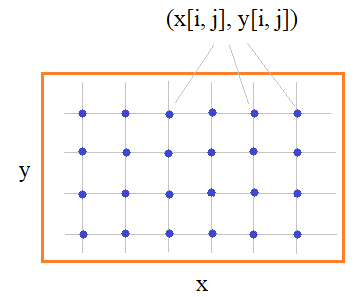
Первое, что нам здесь нужно сделать – это сформировать двумерную сетку координат по осям x и y: 
То есть, должны быть сформированы двумерные массивы x, y, которые для текущей точки с индексами (i, j) возвращают ее координаты в плоскости xy. Для регулярных сеток эти массивы можно сформировать следующим образом. Определим множество координат x (для столбцов) и y (для строк), например, так:
xgrid, ygrid = np.meshgrid(x, y)
На выходе получим двумерные массивы со значениями: То есть, смотрите, теперь для любой пары индексов (i, j) мы легко сможем получить координаты точки в плоскости xy:
(xgrid[1, 2], ygrid[1, 2]) = (3, 5) (xgrid[3, 0], ygrid[3, 0]) = (1, 8)
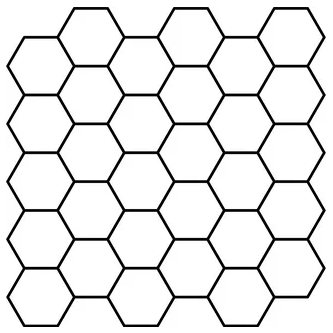
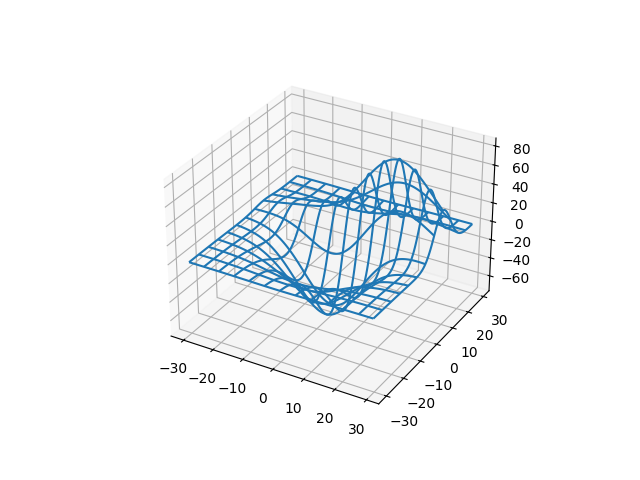
Но зачем было так все усложнять? Почему бы не использовать одномерные массивы x, y вместо двумерных xgrid, ygrid? Дело в том, что одномерные массивы, которые описывают расположение строк и столбов, могут формировать только регулярные сетки, то есть, прямоугольные. А что, если нужно сформировать гексагональную сетку, которая выглядит, следующим образом: Здесь уже не получится обойтись указанными одномерными массивами, а нужно прописывать узлы двумерными массивами. Именно поэтому, в общем случае, и реализовано отображение через двумерные массивы трехмерных графиков. Итак, давайте теперь построим полноценный трехмерный график синусоиды на регулярной сетке. Для этого мы сначала сформируем координаты узлов в плоскости xy:
x = np.arange(-2*np.pi, 2*np.pi, 0.2) y = np.arange(-2*np.pi, 2*np.pi, 0.2) xgrid, ygrid = np.meshgrid(x, y)
zgrid = np.sin(xgrid) * np.sin(ygrid) / (xgrid * ygrid)
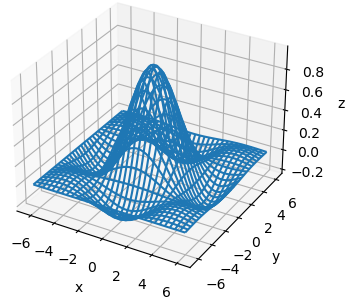
ax_3d.plot_wireframe(xgrid, ygrid, zgrid)
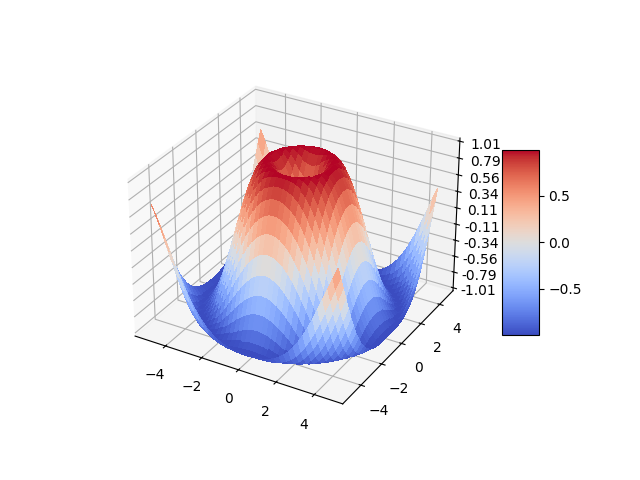
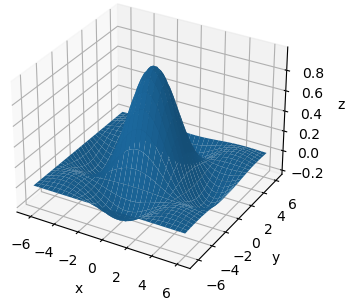
то результат будет следующий: Как видите, мы получили полноценный каркасный трехмерный график синусоиды. Или же можно построить полноценную поверхность в виде синусоиды, используя функцию plot_surface():
ax_3d.plot_surface(xgrid, ygrid, zgrid)
Фактически, только этим две эти функции и отличаются друг от друга: первая строит 3D-каркас, а вторая 3D-поверхность. У этих функций есть следующие параметры для настройки внешнего вида графика:
| Параметр | Описание |
| x, y, z | 2D массивы для построения трехмерных графиков. |
| rcount, ccount | Максимальное число элементов каркаса по координатам x и y (по умолчанию 50). |
| rstride, cstride | Величина шага, с которым будут выбираться элементы из массивов x, y (параметры rstride, cstride и rcount, ccount – взаимоисключающие). |
| color | Цвет графика |
| cmap | Цветовая карта графика |
Например, если установить параметры:
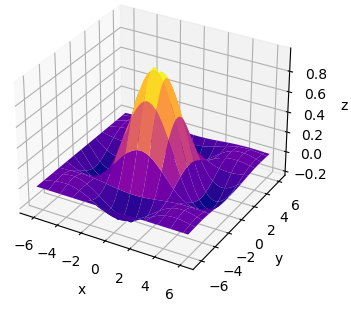
ax_3d.plot_surface(xgrid, ygrid, zgrid, rstride=5, cstride=5, cmap='plasma')
то получим следующий вид нашей синусоиды: В заключение этого занятия приведу пример построения этого же графика набором точек, используя функцию scatter():
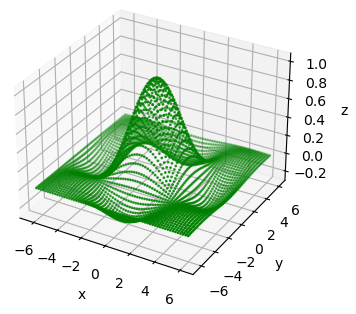
ax_3d.scatter(xgrid, ygrid, zgrid, s=1, color='g')
Увидим следующий результат: Вот так в базовом варианте можно выполнять построения трехмерных графиков в пакете matplotlib. Этой информации достаточно для большинства прикладных задач. Ну а если потребуется реализовать что-то особенное, тогда прямой путь к документации: https://matplotlib.org/stable/api/_as_gen/mpl_toolkits.mplot3d.axes3d.Axes3D.html
The mplot3d toolkit#
This tutorial showcases various 3D plots. Click on the figures to see each full gallery example with the code that generates the figures.
3D Axes (of class Axes3D ) are created by passing the projection=»3d» keyword argument to Figure.add_subplot :
import matplotlib.pyplot as plt fig = plt.figure() ax = fig.add_subplot(projection='3d')
Multiple 3D subplots can be added on the same figure, as for 2D subplots.
Changed in version 3.2.0: Prior to Matplotlib 3.2.0, it was necessary to explicitly import the mpl_toolkits.mplot3d module to make the ‘3d’ projection to Figure.add_subplot .
See the mplot3d FAQ for more information about the mplot3d toolkit.
Line plots#
See Axes3D.plot for API documentation.
Scatter plots#
See Axes3D.scatter for API documentation.
Wireframe plots#
See Axes3D.plot_wireframe for API documentation.
Surface plots#
See Axes3D.plot_surface for API documentation.
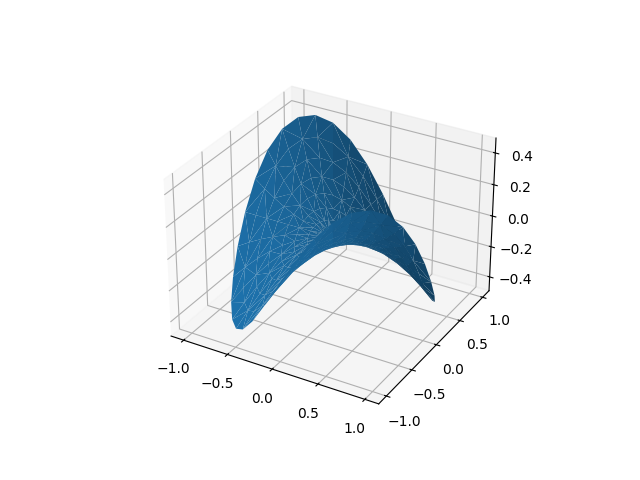
Tri-Surface plots#
See Axes3D.plot_trisurf for API documentation.
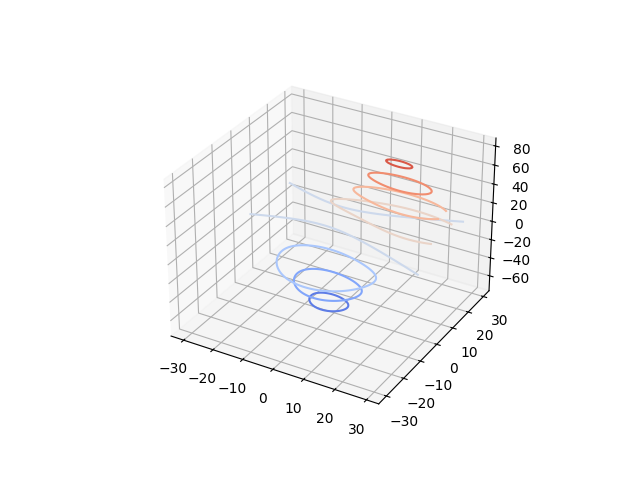
Contour plots#
See Axes3D.contour for API documentation.
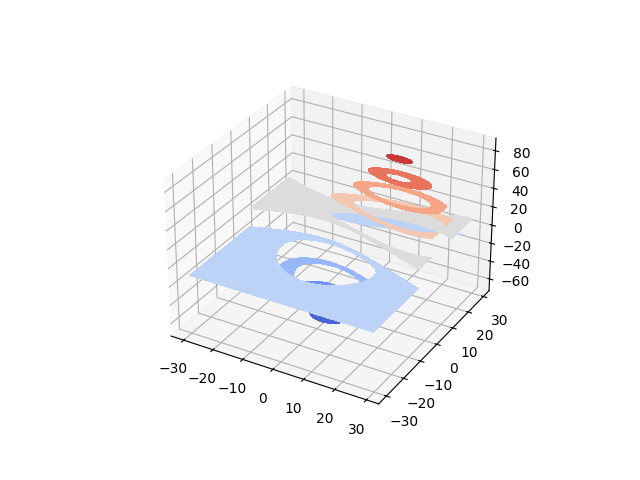
Filled contour plots#
See Axes3D.contourf for API documentation.
New in version 1.1.0: The feature demoed in the second contourf3d example was enabled as a result of a bugfix for version 1.1.0.
Polygon plots#
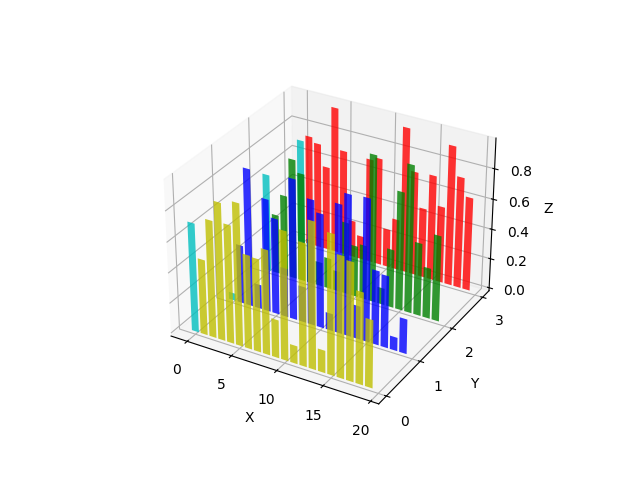
Bar plots#
See Axes3D.bar for API documentation.
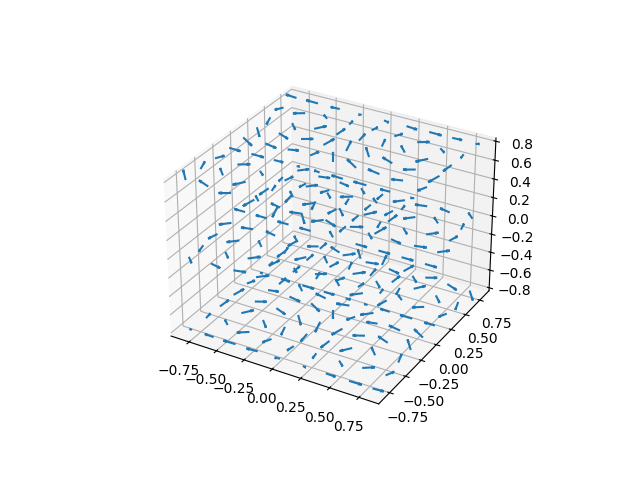
Quiver#
See Axes3D.quiver for API documentation.
2D plots in 3D#
Text#
See Axes3D.text for API documentation.
Three-Dimensional Plotting in Matplotlib
Matplotlib was initially designed with only two-dimensional plotting in mind. Around the time of the 1.0 release, some three-dimensional plotting utilities were built on top of Matplotlib’s two-dimensional display, and the result is a convenient (if somewhat limited) set of tools for three-dimensional data visualization. three-dimensional plots are enabled by importing the mplot3d toolkit, included with the main Matplotlib installation:
from mpl_toolkits import mplot3d
Once this submodule is imported, a three-dimensional axes can be created by passing the keyword projection=’3d’ to any of the normal axes creation routines:
%matplotlib inline import numpy as np import matplotlib.pyplot as plt
fig = plt.figure() ax = plt.axes(projection='3d')
With this three-dimensional axes enabled, we can now plot a variety of three-dimensional plot types. Three-dimensional plotting is one of the functionalities that benefits immensely from viewing figures interactively rather than statically in the notebook; recall that to use interactive figures, you can use %matplotlib notebook rather than %matplotlib inline when running this code.
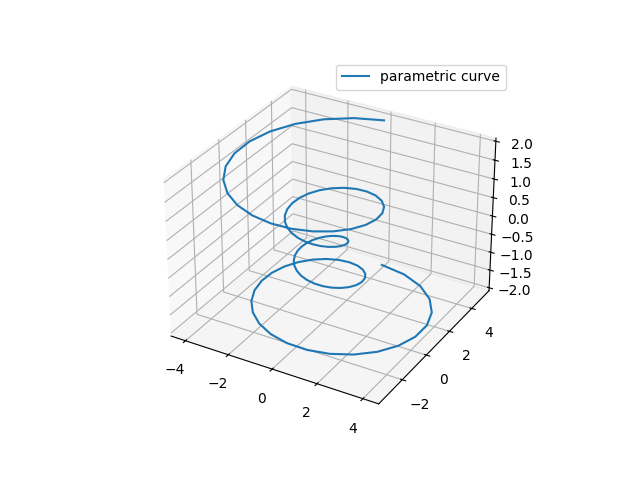
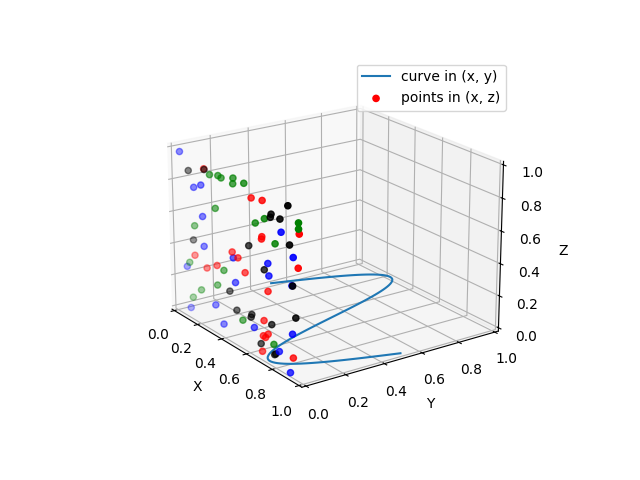
Three-dimensional Points and Lines¶
The most basic three-dimensional plot is a line or collection of scatter plot created from sets of (x, y, z) triples. In analogy with the more common two-dimensional plots discussed earlier, these can be created using the ax.plot3D and ax.scatter3D functions. The call signature for these is nearly identical to that of their two-dimensional counterparts, so you can refer to Simple Line Plots and Simple Scatter Plots for more information on controlling the output. Here we’ll plot a trigonometric spiral, along with some points drawn randomly near the line:
ax = plt.axes(projection='3d') # Data for a three-dimensional line zline = np.linspace(0, 15, 1000) xline = np.sin(zline) yline = np.cos(zline) ax.plot3D(xline, yline, zline, 'gray') # Data for three-dimensional scattered points zdata = 15 * np.random.random(100) xdata = np.sin(zdata) + 0.1 * np.random.randn(100) ydata = np.cos(zdata) + 0.1 * np.random.randn(100) ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens');