Решение производственной задачи в Excel 2007 и новее
В данном разделе мы рассмотрим, как можно решить производственную задачу в программе Microsoft Excel версий 2007, 2010, 2013 или 2016. Если у вас более старая версия программы Microsoft Excel, то перейдите в другой раздел.
Итак, запустим Microsoft Excel, и перейдем на вкладку «Данные». Справа должна располагаться кнопка «Поиск решения», как на картинке:
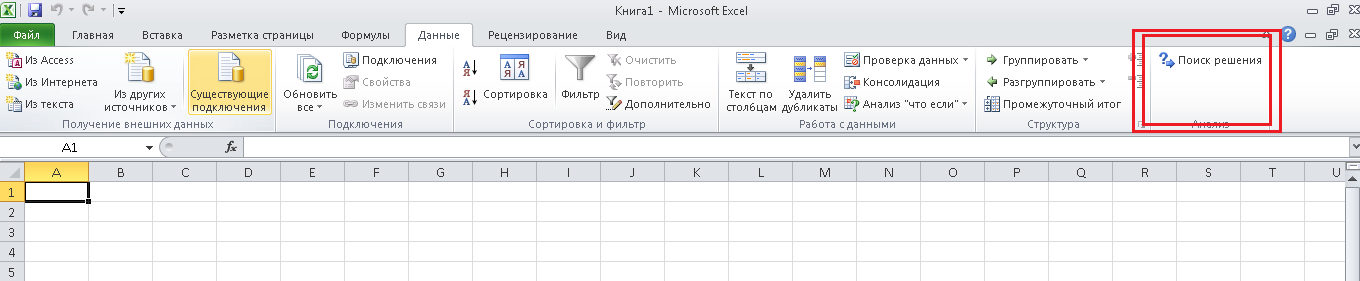
Если же этой кнопки нет, то необходимо включить соответствующую надстройку. Для этого откроем меню файл, и выберем пункт «Параметры»:
В открывшемся меню необходимо выбрать пункт «Надстройки»:
Затем в правой части, внизу, необходимо выбрать из выпадающего списка «Надстройки Excel», если они еще не выбраны, и нажать кнопку «Перейти»:
Появится следующее окно, в котором необходимо отметить галочкой необходимую надстройку (Поиск решения), и нажать кнопку «ОК». После этого на вкладке Данные, в правой части должна появиться показанная выше кнопка
Пример решения ЗЛП в Excel 2010
Возьмем ту же задачу, которую мы решали в предыдущем разделе, и попытаемся решить с помощью компьютера:
| Ресурс | Изделие A | Изделие B | Изделие C | Сколько ресурса на складах |
| R1 | 1 | 2 | 3 | 35 |
| R2 | 2 | 3 | 2 | 45 |
| R3 | 3 | 1 | 1 | 40 |
| Прибыль | 4 | 5 | 6 |
Как мы помним из предыдущего раздела, наши ограничения и целевая функция выглядят следующим образом
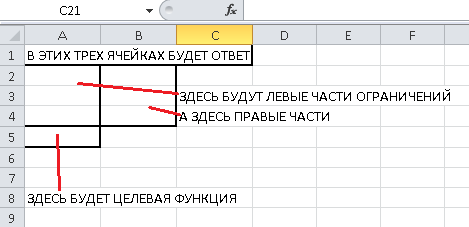
Мы будем заносить данные в следующие ячейки листа Excel:
Итак, начнем заполнение. В верхние три ячейки нужно занести ответ, то есть, количество производимых изделий A, B и C. Так как ответ мы не знаем (а иначе зачем бы мы задачу решали), то пока занесем туда три нуля:
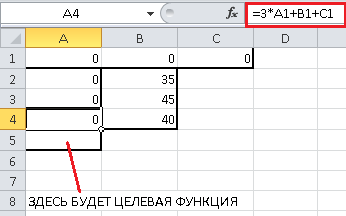
Занесем левые и правые части ограничений в соответствующие ячейки. Например, для первого ограничения $ + 2 + 3 \le 35$ нам нужно занести в ячейку A2 формулу «=A1+2*B1+3*C1», а в ячейку B2 — правую часть ограничения — 35. Точно так же занесем и два других ограничения. Не стоит пугаться, что в ячейках A2-A4 пока будут нули — это естественно, так как пока наше «решение» состоит в том, чтобы не производить ни одного изделия. Должно получиться следующее (красным цветом выделено значение ячейки A4, то есть, третье ограничение $3 + + \le 40$):
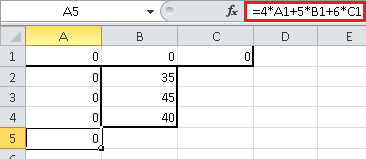
Точно так же, в ячейку A5 занесем формулу для целевой функции $F(,,) = 4 + 5 + 6$ — в Excel это будет формула «=4*A1+5*B1+6*C1». Точно так же, не обращаем внимания, что результатом будет 0 — это естественно, ведь целевая функция представляет из себя прибыль предприятия, а раз мы ничего не производим, то естественно, получаем нулевую прибыль:
Мы занесли все необходимые данные, теперь необходимо выполнить поиск решения. Для этого на вкладке «Данные» нажимаем кнопку «Поиск решения». Видим следующее окно:
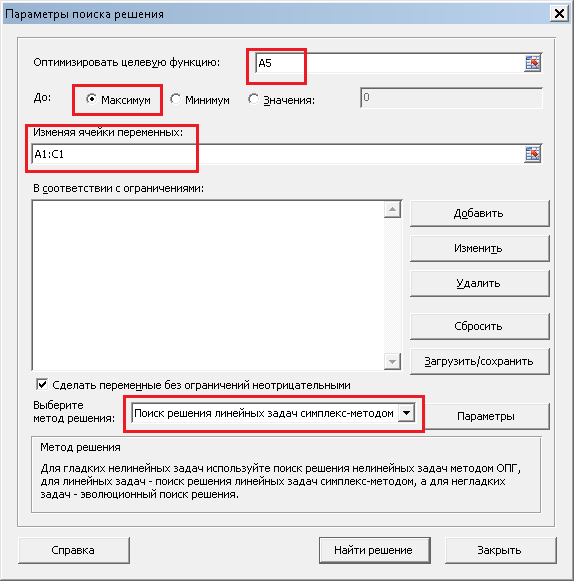
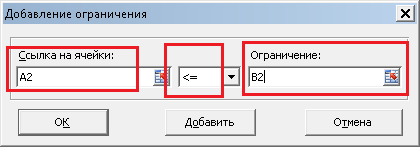
В поле «Оптимизировать целевую функцию» записываем A5, так как именно в ячейке A5 у нас записана целевая функция. На следующей строке выбираем «Максимум», так как нам необходимо максимизировать целевую функцию, то есть, прибыль. В поле «Изменяя ячейки переменных» записываем A1:C1, так как в ячейках A1, B1 и C1 у нас количество производимых товаров, которые необходимо подобрать. В поле «Выберите метод решения» выбираем «Поиск решения линейных задач симплекс-методом». Теперь необходимо задать ограничения. Для этого нажимаем на кнопку «Добавить», и пишем (для первого ограничения) следующее:
То есть, говорим, что значение ячейки A2 (первое ограничение) должно быть «меньше или равно» значению ячейки B2 (правой части первого ограничения). Нажимаем OK, и ограничение добавится в список. Таким же образом добавляем два других ограничения, а также еще три ограничения — что наши переменные должны быть больше или равны нулю. Должно получиться следующее:
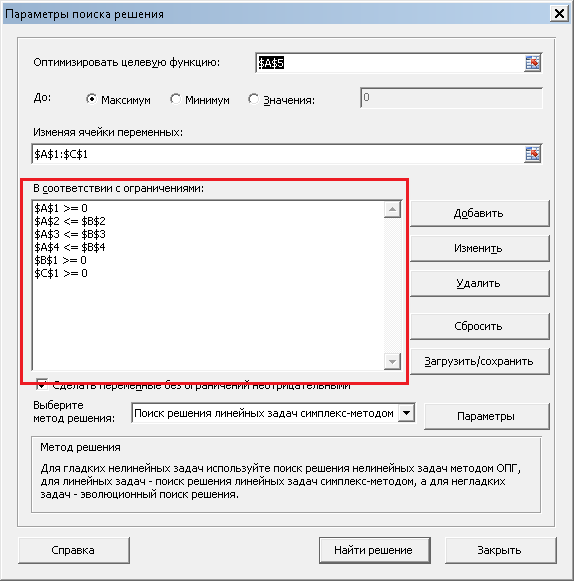
Задача почти решена. Просто нажимаем кнопку «Найти решение», и появляется окно, в котором нам сообщают, что задача решена (решение найдено), а также спрашивают, хотим ли мы его сохранить:
Нажимаем OK, и видим решение в ячейках A1, B1, C1:
В ячейке A1 мы видим число 10 — число изделий A, которые необходимо произвести, в ячейке A2 — число 5 — число изделий B, которые необходимо произвести, а в ячейке A3 — число 5 — число изделий C, которые необходимо произвести. То есть, мы получили решение (10;5;5) — такое же, как и в предыдущем разделе. Кроме того, в ячейке A5 мы видим максимальное значение целевой функции — тоже, такое же, как и в предыдущем разделе. Задача решена верно.
Конечно, мы решили задачу совсем без оформления. Если вам нужно решить такую задачу для сдачи в университет, то вы можете оформить ее, например, так:
Итоги
Мы научились решать производственную задачу с помощью надстройки Excel под названием «Поиск решения». В следующем разделе мы рассмотрим решение целочисленной производственной задачи, то есть задачи ЛП с дополнительным ограничением — все значения переменных должны быть целыми.
Полезное по теме
Решение задач линейного программирования в Excel
Изучив алгоритмы «ручного» решения задач линейного программирования, полезно познакомиться и со способом упростить этот процесс. Ясно, что чем сложнее задача, чем больше в ней переменных и условий, тем утомительнее и дольше ее решать. В таких случаях удобно использовать специальные математические пакеты, или доступную многим программу MS Excel (версии 2003, 2007, 2010, 2013 и др.).
Решить задачи линейного программирования в Excel достаточно просто:
- составить математическую модель задачи,
- внести исходные данные задачи и ограничения,
- выделить место под ячейки решения и целевую функцию, ввести ее формулу,
- запустить надстройку Поиск решения,
- установить нужные параметры решения и запустить выполнение.
Программа подберёт оптимальное решение и покажет его в нужных ячейках, вычислит значение целевой функции. При необходимости можно построить отчеты для анализа решения задачи.
Подробнее все эти этапы с пояснениями и скриншотами разобраны ниже в примерах на разных задачах линейного программирования — изучайте, ищите похожие, решайте.
Линейное программирование: примеры в Excel
Задача 1. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать выводы по полученным результатам.
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.
Задача 2. Цех производит 8 различных видов деталей для двигателей A, B, C1, C2, C3, D, E6, F имея в своем распоряжении перечисленный ниже парк из 7 видов универсальных станков: 2 шт. -ADF, 3 шт. -SHG, 3 шт. -BSD, 1 шт. -AVP, 1 шт. -BFG, 3 шт. -ABM, 2 шт. -RL.
Время, требуемое для обработки единицы каждого продукта на каждом станке, вклад в прибыль от производства единицы каждого продукта и рыночный спрос на каждый продукт за месяц даны в таблице.
Цех работает 12 часов в день. Каждый месяц содержит 26 рабочих дней. Для упрощения задачи считаем, что возможен произвольный порядок обработки деталей на различных станках.
Составьте оптимальный план производства.
Определите, производство каких продуктов лимитировано рынком, и каких – техническими возможностями цеха. Какие машинные ресурсы должны быть увеличены в первую очередь, чтобы добиться максимального увеличения прибыли (при заданных потребностях рынка)?
Есть ли продукт, который невыгодно производить? Почему? Что нужно изменить, чтобы все продукты стало выгодно производить?
Задача 3. Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов — К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в таблице.
Задача 4. Фирма «Компьютер-сервис» поставляет компьютеры под ключ четырех базовых комплектаций: «домашний», «игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.
Задача 5. На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?
Задача 6. Компания «Евростройтур» организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию. Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута).
Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.
Задача 7. Решить задачу методом ветвей и границ, решая отдельные задачи линейного нецелочисленного программирования с помощью функции «Поиск решения» в Microsoft Excel (в случае, если первая же задача ЛП выдает целочисленное решение, не позволяя ветвить задачу, немного изменить начальные условия).
Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?
Задача 8. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить a11 кг сырья первого типа, a21 кг сырья второго типа, a31 кг сырья третьего типа.
На изготовление единицы Изделия 2 требуется затратить a12 кг сырья первого типа, a22 кг сырья второго типа, a32 кг сырья третьего типа.
Производство обеспечено сырьем каждого типа в количестве b1 кг, b2 кг, b3 кг соответственно.
Рыночная цена единицы Изделия 1 составляет c1 тыс. руб., а единицы Изделия 2 — c2 тыс.руб.
Требуется:
1) построить экономико – математическую модель задачи;
2) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.
3) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи табличного симплекс – метода решения задачи линейного программирования.
4) составить план производства изделий, обеспечивающий максимальную выручку от их реализации, используя надстройку «Поиск решения» в среде MS EXCEL.