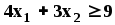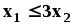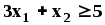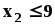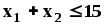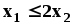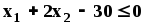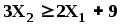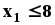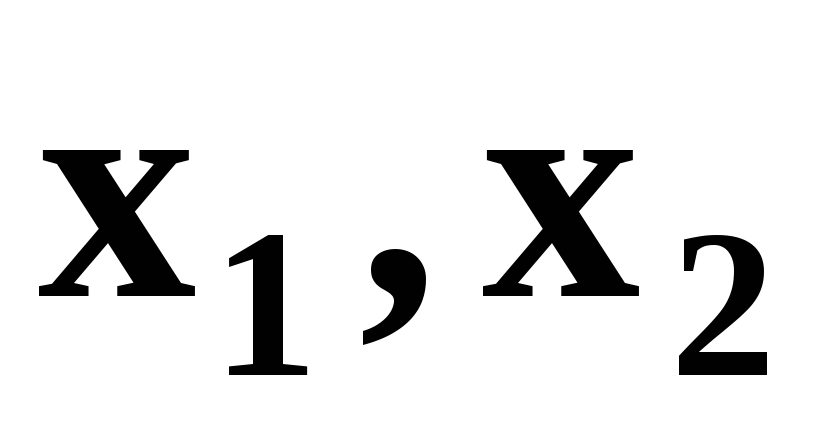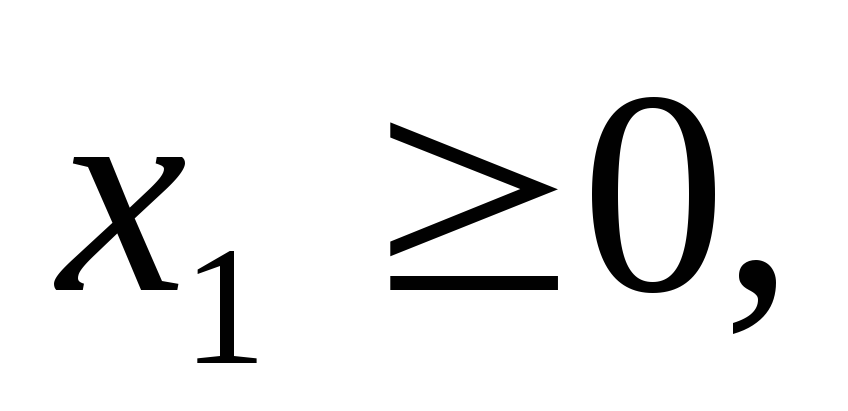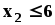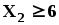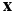5. Многомерная оптимизация. Линейное программирование
Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Количественная оценка оптимизируемого качества называется критерием оптимальности или целевой функцией. Её можно записать в виде:
, (5.1)
где –некоторые параметры объекта оптимизации.
Существуют два типа задач оптимизации – безусловные и условные.
Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (5.1) от n действительных переменных и определении соответствующих значений аргументов.
Условные задачи оптимизации, или задачи с ограничениями, — это такие, при формулировке которых на значения аргументов налагаются ограничения в виде равенств или неравенств.
Решение задач оптимизации, в которых критерий оптимальности является линейной функцией независимых переменных (то есть содержит эти переменные в первой степени) с линейными ограничениями на них, составляет предмет линейного программирования.
Слово «программирование» отражает здесь конечную цель исследования – определение оптимального плана или оптимальной программы, по которой из множества возможных вариантов исследуемого процесса выбирают по какому-либо признаку наилучший, оптимальный, вариант.
Примером такой задачи является задача оптимального распределения сырья между различными производствами при максимальной стоимости продукции.
Пусть из двух видов сырья изготавливается продукция двух видов.
–число единиц продукции первого и второго вида, соответственно;
–цена единицы продукции первого и второго вида, соответственно.
Тогда общая стоимость всей продукции будет
. (5.2)
В результате производства желательно, чтобы общая стоимость продукции была максимальной. – целевая функция в данной задаче.
–количество сырья первого и второго видов, имеющееся в наличии;
–число единиц i-го вида сырья, необходимое для производства единицы j-го вида продукции.
Учитывая, что расход данного ресурса не может превышать общего его количества, запишем ограничительные условия по ресурсам:
Относительно переменных можно ещё сказать, что они неотрицательны и не бесконечны.:
Среди множества решений системы неравенств (5.3) и (5.4) требуется найти такое решение (), для которого функция R достигает наибольшего значения.
В аналогичном виде формулируются так называемые транспортные задачи (задачи оптимальной организации доставки товаров, сырья или продукции из различных складов к нескольким пунктам назначения при минимуме затрат на перевозку) и ряд других.
Графический метод решения задачи линейного программирования.
Пусть требуется найти 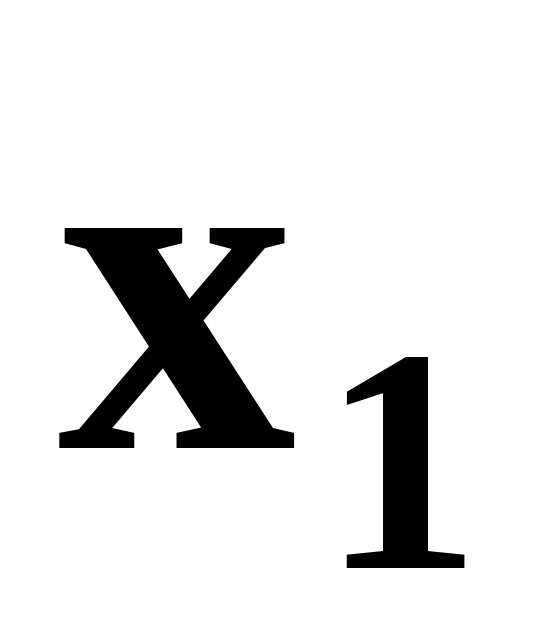
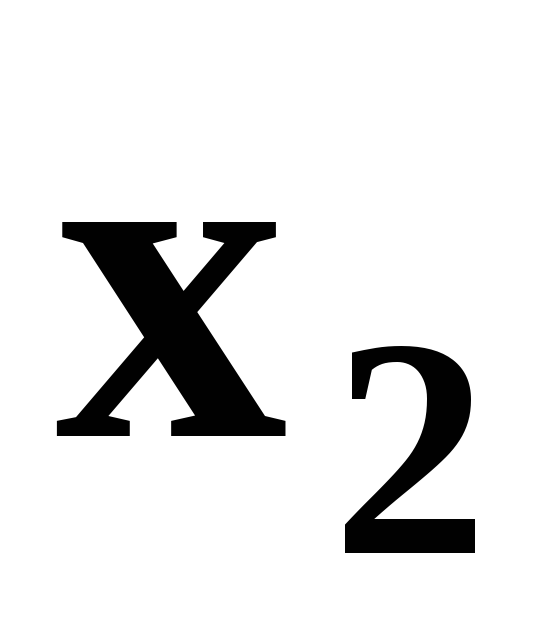
(5.5)
и условиям неотрицательности

(5.7)
Построим в системе прямоугольных координат 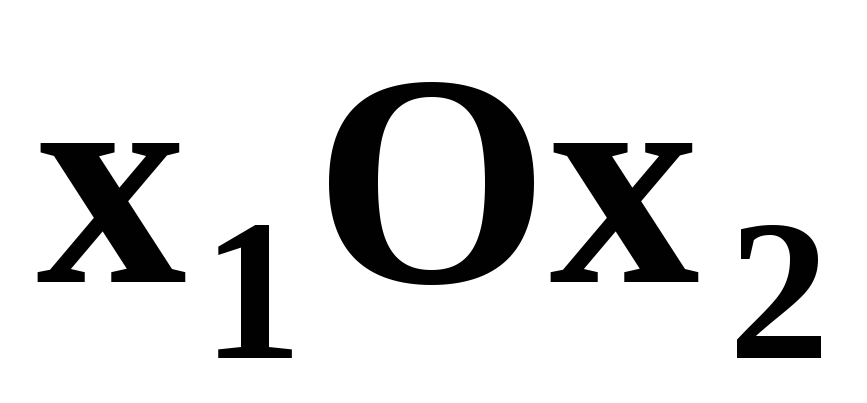
Эта прямая делит плоскость 




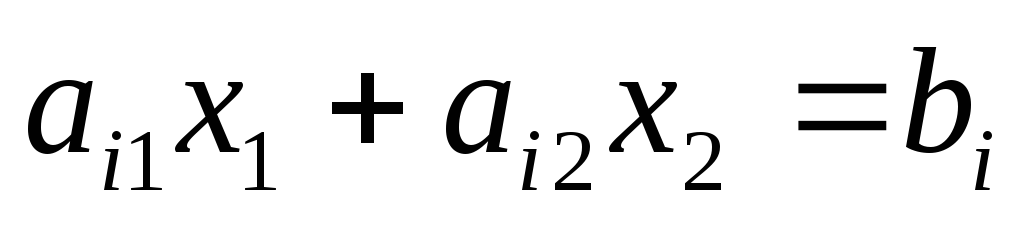
Для определения того, по какую сторону от граничной прямой располагается полуплоскость, соответствующая заданному неравенству, достаточно «испытать» одну какую-либо точку (проще всего точку О (0;0)). Если при подстановке её координат в левую часть неравенства оно удовлетворяется, то полуплоскость обращена в сторону к испытуемой точке, если же неравенство не удовлетворяется, то соответствующая полуплоскость обращена в противоположную сторону. Направление полуплоскости показывается на чертеже штриховкой. Неравенствам 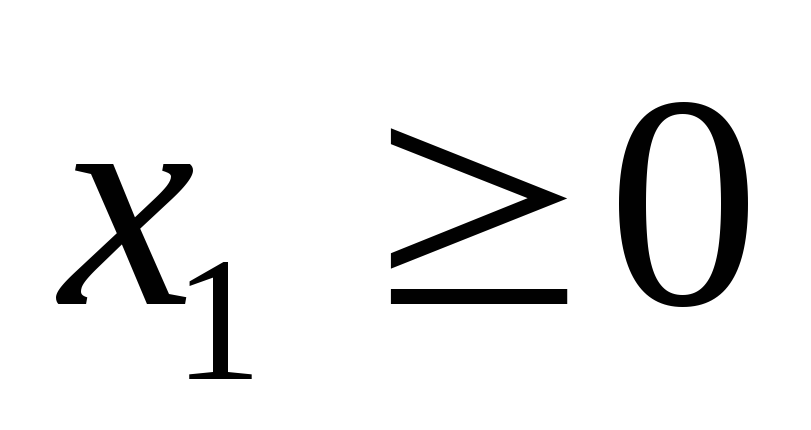

На рисунке строим граничные прямые и полуплоскости, соответствующие всем неравенствам.
Общая, часть (пересечение) всех этих полуплоскостей будет представлять собой область допустимых решений данной задачи.
При построении области допустимых решений в зависимости от конкретного вида системы ограничений (неравенств) на переменные может встретиться один из следующих четырех случаев:
Рис. 12. Область допустимых решений пустая, что соответствует несовместности системы неравенств; решения нет.
Рис. 13. Область допустимых решений изобра- жается одной точкой А, что соответствует единственному решению системы.
Рис. 14. Область допустимых решений ограниченная, изображается в виде выпуклого многоугольника. Допустимых решений бесконечное множество.
Рис. 15. Область допустимых решений неограни-ченная, в виде выпуклой многоугольной области. Допустимых решений бесконечное множество.
Графическое изображение целевой функции при фиксированном значенииR определяет прямую, а при изменении R — семейство параллельных прямых с параметром R. Для всех точек, лежащих на одной из прямых, функция R принимает одно определенное значение, поэтому указанные прямые называются линиями уровня для функции R.
Вектор градиента , перпендикулярный к линиям уровня, показывает направление возрастанияR.
Задача отыскания оптимального решения системы неравенств (5.5), для которого целевая функцияR (5.7) достигает максимума, геометрически сводится к определению в области допустимых решений точки, через которую пройдет линия уровня, соответствующая наибольшему значении параметра R
Если область допустимых решений есть выпуклый многоугольник, то экстремум функции R достигается, по крайней мере, в одной из вершин этого многоугольника.
Если экстремальное значение R достигается в двух вершинах, ‘то такое же экстремальное значение достигается в любой точке на отрезке, соединяющем эти две вершины. В этом случае говорят, что задача имеет альтернативный оптимум.
В случае неограниченной области экстремум функции R либо не существует, либо достигается в одной из вершин области, либо имеет альтернативный оптимум.
Пусть требуется найти значения 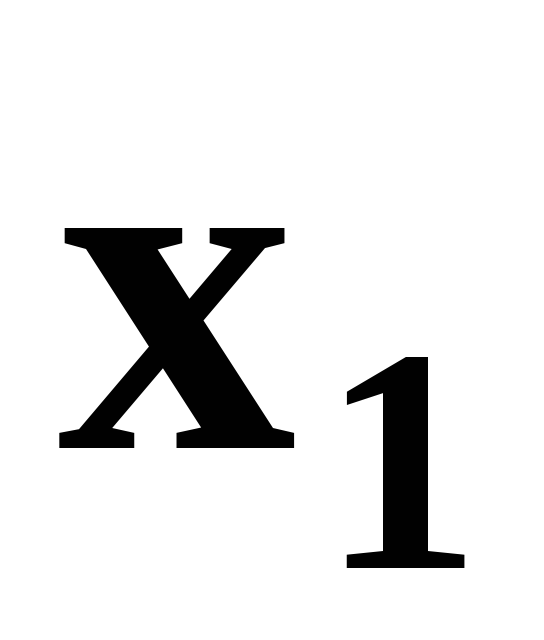

и условиям неотрицательности
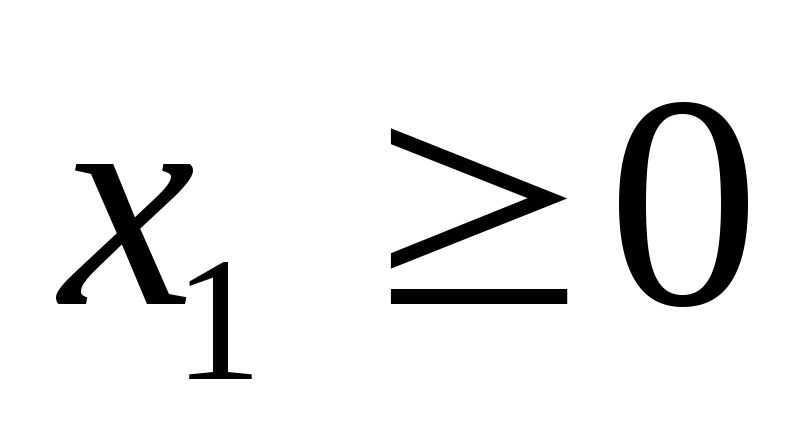

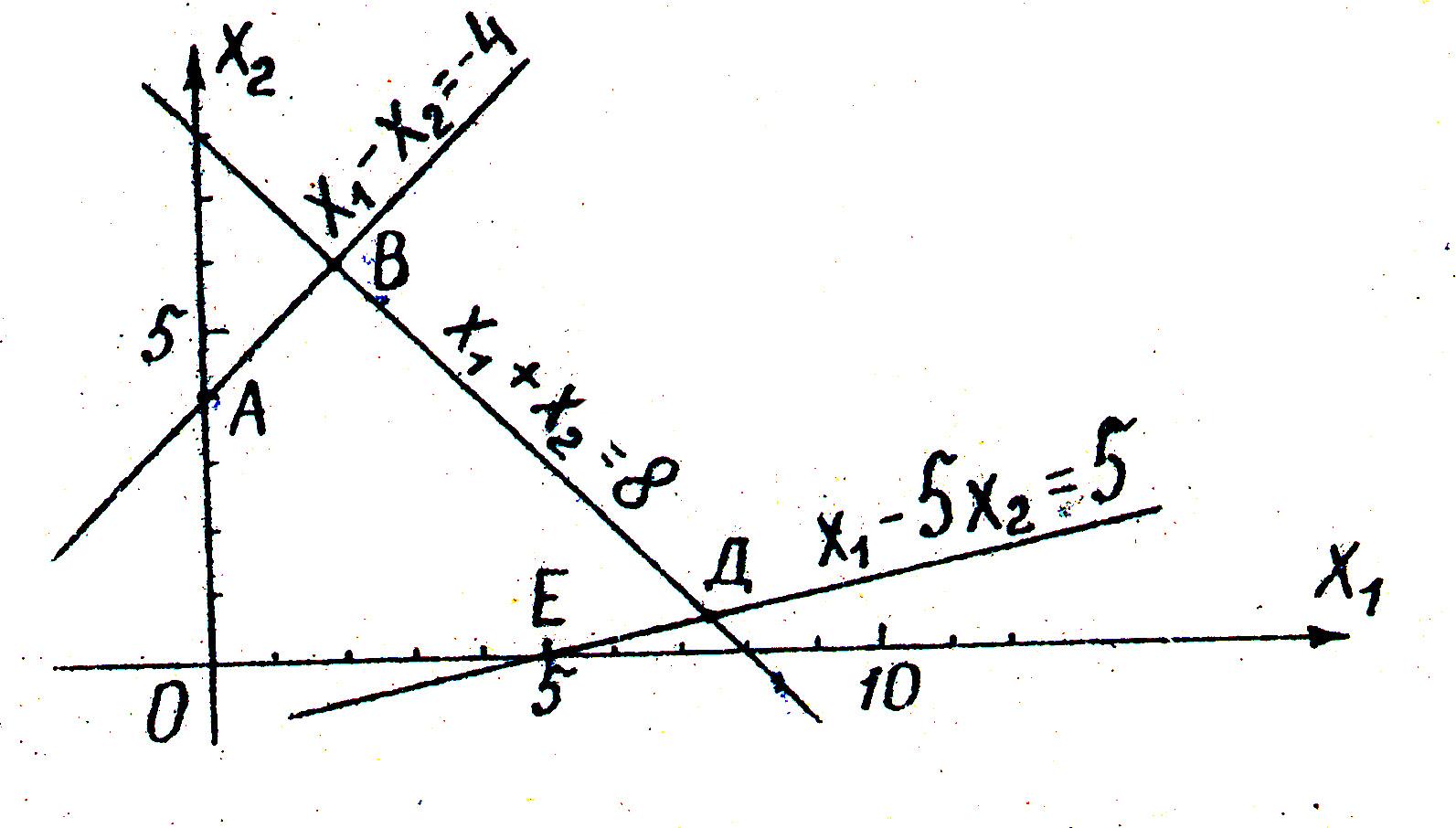
Заменим каждое из неравенств равенством и построим граничные прямые:
Определим полуплоскости, соответствующие данным неравенствам, путём «испытания» точки (0;0). С учетом неотрицательности 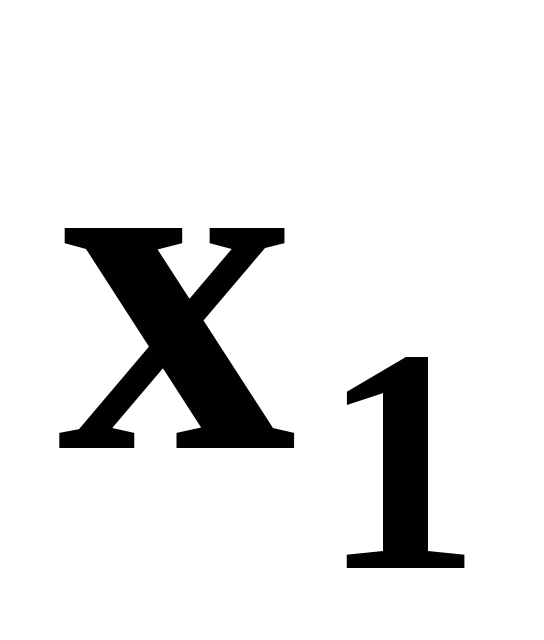

В области допустимых решений находим оптимальное решение, строя вектор градиента , показывающий направление возрастанияR.
Оптимальное решение соответствует точке В, координаты которой можно определить либо графически, либо путем решения системы двух уравнений, соответствующих граничным прямым АВ и ВД:
Ответ:
Задания. Найти положение точки экстремума и экстремальное значение целевой функции при заданных ограничениях.
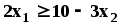

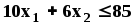




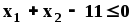


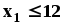

3