Алгоритм Дейкстры
Алгоритм Дейкстры (англ. Dijkstra’s algorithm) находит кратчайшие пути от заданной вершины $s$ до всех остальных в графе без ребер отрицательного веса.
Существует два основных варианта алгоритма, время работы которых составляет $O(n^2)$ и $O(m \log n)$, где $n$ — число вершин, а $m$ — число ребер.
#Основная идея
Заведём массив $d$, в котором для каждой вершины $v$ будем хранить текущую длину $d_v$ кратчайшего пути из $s$ в $v$. Изначально $d_s = 0$, а для всех остальных вершин расстояние равно бесконечности (или любому числу, которое заведомо больше максимально возможного расстояния).
Во время работы алгоритма мы будем постепенно обновлять этот массив, находя более оптимальные пути к вершинам и уменьшая расстояние до них. Когда мы узнаем, что найденный путь до какой-то вершины $v$ оптимальный, мы будем помечать эту вершину, поставив единицу ($a_v=1$) в специальном массиве $a$, изначально заполненном нулями.
Сам алгоритм состоит из $n$ итераций, на каждой из которых выбирается вершина $v$ с наименьшей величиной $d_v$ среди ещё не помеченных:
(Заметим, что на первой итерации выбрана будет стартовая вершина $s$.)
Выбранная вершина отмечается в массиве $a$, после чего из из вершины $v$ производятся релаксации: просматриваем все исходящие рёбра $(v,u)$ и для каждой такой вершины $u$ пытаемся улучшить значение $d_u$, выполнив присвоение
.</p><script data-noptimize=) /*
/*
Для начала отметим, что для любой вершины $v$ всегда выполняется $d_v \ge l_v$: алгоритм не может найти путь короче, чем кратчайший из всех существующих (ввиду того, что мы не делали ничего кроме релаксаций).
Доказательство корректности самого алгоритма основывается на следующем утверждении.
Утверждение. После того, как какая-либо вершина $v$ становится помеченной, текущее расстояние до неё $d_v$ уже является кратчайшим, и, соответственно, больше меняться не будет.
Доказательство будем производить по индукции. Для первой итерации его справедливость очевидна — для вершины $s$ имеем $d_s=0$, что и является длиной кратчайшего пути до неё.
Пусть теперь это утверждение выполнено для всех предыдущих итераций — то есть всех уже помеченных вершин. Докажем, что оно не нарушается после выполнения текущей итерации, то есть что для выбранной вершины $v$ длина кратчайшего пути до неё $l_v$ действительно равна $d_v$.
Рассмотрим любой кратчайший путь до вершины $v$. Обозначим первую непомеченную вершину на этом пути за $y$, а предшествующую ей помеченную за $x$ (они будут существовать, потому что вершина $s$ помечена, а вершина $v$ — нет). Обозначим вес ребра $(x, y)$ за $w$.
$: на каждой итерации мы находим аргминимум за $O(n)$ и проводим $O(n)$ релаксаций.</pre><p>Заметим также, что мы можем делать не $n$ итераций а чуть меньше. Во-первых, последнюю итерацию можно никогда не делать (оттуда ничего уже не прорелаксируешь). Во-вторых, можно сразу завершаться, когда мы доходим до недостижимых вершин ($d_v = \infty$).</p><h3>#Для разреженных графов</h3><p>Если $m \approx n$, то минимум можно искать быстрее. Вместо линейного прохода заведем структуру, в которую можно добавлять элементы и искать минимум — например std::set так умеет.</p><p>Будем поддерживать в этой структуре пары $(d_v, v)$, при релаксации удаляя старый $(d_u, u)$ и добавляя новый $(d_v + w, u)$, а при нахождении оптимального $v$ просто беря минимум (первый элемент).</p><p>Поддерживать массив $a$ нам теперь не нужно: сама структура для нахождения минимума будет играть роль множества ещё не рассмотренных вершин.</p><pre>Для каждого ребра нужно сделать два запроса в двоичное дерево, хранящее $O(n)$ элементов, за $O(\log n)$ каждый, поэтому асимптотика такого алгоритма составит $O(m \log n)$. Заметим, что в случае полных графов это будет равно $O(n^2 \log n)$, так что про предыдущий алгоритм забывать не стоит.</pre><h3>#С кучей</h3><p>Вместо двоичного дерева «правильнее» использовать более специализированную структуру, которая поддерживает именно добавление элементов и нахождение минимума: кучу. Удалять произвольные элементы в ней немного сложнее, поэтому вместо этого будем просто игнорировать все повторные вершины.</p><pre><span <span <span <span <span <span <span <span <span <span <span объявим очередь с приоритетами для *минимума* (по умолчанию ищется максимум)</span> </span></span><span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span >На практике вариант с priority_queue немного быстрее.</pre><p>Помимо обычной двоичной кучи, можно использовать и другие. С теоретической точки зрения, особенно интересна Фибоначчиева куча: у неё все почти все операции кроме работают за $O(1)$, но удаление элементов — за $O(\log n)$. Это позволяет облегчить релаксирование до $O(1)$ за счет увеличения времени извлечения минимума до $O(\log n)$, что приводит к асимптотике $O(n \log n + m)$ вместо $O(m \log n)$.</p><h3>#Восстановление путей</h3><p>Часто нужно знать не только длины кратчайших путей, но и получить сами пути.</p><p>Для этого можно создать массив $p$, в котором в ячейке $p_v$ будет хранится <em>родитель</em> вершины $v$ — вершина, из которой произошла последняя релаксация по ребру $(p_v, v)$.</p><p>Обновлять его можно параллельно с массивом $d$. Например, в последней реализации:</p><pre><span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <span <-- кратчайший путь в u идет через ребро (v, u)</span> </span></span><span <span <span >Для восстановления пути нужно просто пройтись по предкам вершины $v$:</pre><pre>Обратим внимание, что код распечатает путь в обратном порядке.</pre><p><a href=) Источник
Источник
Алгоритм Дейкстры. Поиск оптимальных маршрутов на графе
Из многих алгоритмов поиска кратчайших маршрутов на графе, на Хабре я нашел только описание алгоритма Флойда-Уоршалла. Этот алгоритм находит кратчайшие пути между всеми вершинами графа и их длину. В этой статье я опишу принцип работы алгоритма Дейкстры, который находит оптимальные маршруты и их длину между одной конкретной вершиной (источником) и всеми остальными вершинами графа. Недостаток данного алгоритма в том, что он будет некорректно работать если граф имеет дуги отрицательного веса.
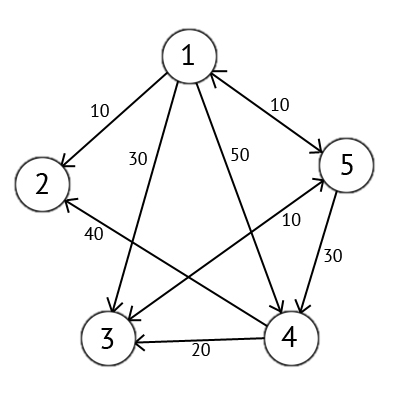
Для примера возьмем такой ориентированный граф G:
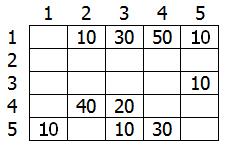
Этот граф мы можем представить в виде матрицы С:
Возьмем в качестве источника вершину 1. Это значит что мы будем искать кратчайшие маршруты из вершины 1 в вершины 2, 3, 4 и 5.
Данный алгоритм пошагово перебирает все вершины графа и назначает им метки, которые являются известным минимальным расстоянием от вершины источника до конкретной вершины. Рассмотрим этот алгоритм на примере.
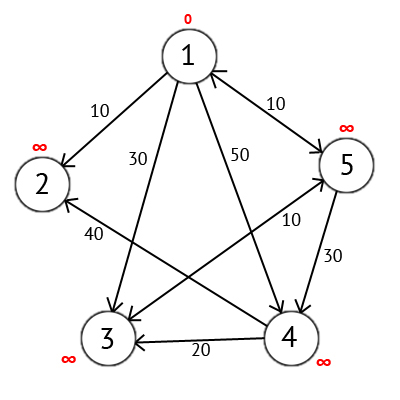
Присвоим 1-й вершине метку равную 0, потому как эта вершина — источник. Остальным вершинам присвоим метки равные бесконечности.
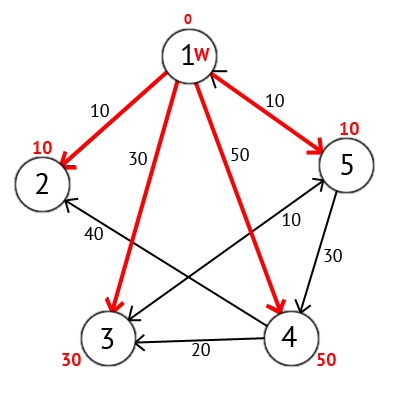
Далее выберем такую вершину W, которая имеет минимальную метку (сейчас это вершина 1) и рассмотрим все вершины в которые из вершины W есть путь, не содержащий вершин посредников. Каждой из рассмотренных вершин назначим метку равную сумме метки W и длинны пути из W в рассматриваемую вершину, но только в том случае, если полученная сумма будет меньше предыдущего значения метки. Если же сумма не будет меньше, то оставляем предыдущую метку без изменений.
После того как мы рассмотрели все вершины, в которые есть прямой путь из W, вершину W мы отмечаем как посещённую, и выбираем из ещё не посещенных такую, которая имеет минимальное значение метки, она и будет следующей вершиной W. В данном случае это вершина 2 или 5. Если есть несколько вершин с одинаковыми метками, то не имеет значения какую из них мы выберем как W.
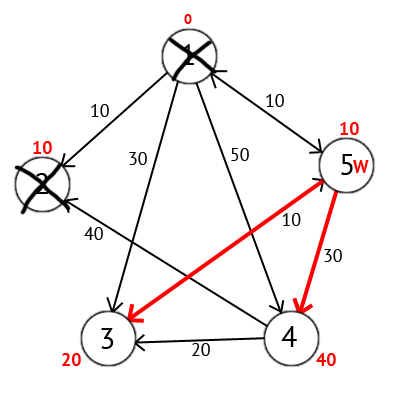
Мы выберем вершину 2. Но из нее нет ни одного исходящего пути, поэтому мы сразу отмечаем эту вершину как посещенную и переходим к следующей вершине с минимальной меткой. На этот раз только вершина 5 имеет минимальную метку. Рассмотрим все вершины в которые есть прямые пути из 5, но которые ещё не помечены как посещенные. Снова находим сумму метки вершины W и веса ребра из W в текущую вершину, и если эта сумма будет меньше предыдущей метки, то заменяем значение метки на полученную сумму.
Исходя из картинки мы можем увидеть, что метки 3-ей и 4-ой вершин стали меньше, тоесть был найден более короткий маршрут в эти вершины из вершины источника. Далее отмечаем 5-ю вершину как посещенную и выбираем следующую вершину, которая имеет минимальную метку. Повторяем все перечисленные выше действия до тех пор, пока есть непосещенные вершины.
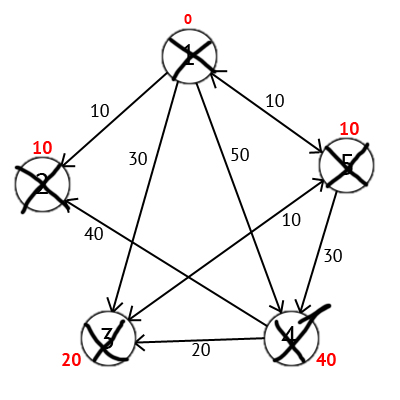
Выполнив все действия получим такой результат:
Также есть вектор Р, исходя из которого можно построить кратчайшие маршруты. По количеству элементов этот вектор равен количеству вершин в графе, Каждый элемент содержит последнюю промежуточную вершину на кратчайшем пути между вершиной-источником и конечной вершиной. В начале алгоритма все элементы вектора Р равны вершине источнику (в нашем случае Р = ). Далее на этапе пересчета значения метки для рассматриваемой вершины, в случае если метка рассматриваемой вершины меняется на меньшую, в массив Р мы записываем значение текущей вершины W. Например: у 3-ей вершины была метка со значением «30», при W=1. Далее при W=5, метка 3-ей вершины изменилась на «20», следовательно мы запишем значение в вектор Р — Р[3]=5. Также при W=5 изменилось значение метки у 4-й вершины (было «50», стало «40»), значит нужно присвоить 4-му элементу вектора Р значение W — P[4]=5. В результате получим вектор Р = .
Зная что в каждом элементе вектора Р записана последняя промежуточная вершина на пути между источником и конечной вершиной, мы можем получить и сам кратчайший маршрут.