Программирование основные алгоритмические структуры

8.3. Базовые алгоритмические структуры

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е. основных) элементов. Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов. Для их описания будем использовать язык схем алгоритмов и школьный алгоритмический язык.

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.

Характерной особенностью базовых структур является наличие в них одного входа и одного выхода. Ниже базовые структуры будут представляться в двух самых наглядных формах на школьном алгоритмическом языке и в графической форме

1. Базовая структура «следование«. Образуется последовательностью действий, следующих одно за другим: Алгоритм, в котором есть структура «следование» называется линейным.

Школьный алгоритмический язык

действие 1 действие 2 . . . . . . . . . действие n

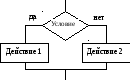
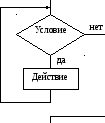
2. Базовая структура «ветвление«. Ветвление – это выбор действия в зависимости от выполнения какого-нибудь условия. Алгоритм, в котором есть структура «ветвление» называется разветвляющимся.

Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. В школьный алгоритмический языке служебное слово если обозначает начало ветвления, а все – конец ветвления.

Структура ветвление существует в четырех основных вариантах:

• если–то;
• если–то–иначе;
• выбор;
• выбор–иначе.

Школьный алгоритмический язык	Язык блок–схем
1. если–то
если условие то действия все Здесь представлена не полная форма ветвления. В этом случае выполнится действие (или группа действий), расположенное в строке то только при соблюдении условия. Если же условие не соблюдается, то исполнитель перейдет к выполнению действий, следующих за служебным словом все.
2. если–то–иначе
если условие то действия 1 иначе действия 2 все Здесь представлена полная форма ветвления. В полной форме в зависимости от условия в строке если выполняется только одно из действий ( или группа действий), расположенных либо в строке то (условие соблюдено), либо в строке иначе (условие не соблюдено).
3. выбор
выборпри условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N все
4. выбор–иначе
выборпри условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N иначе действия N+1 все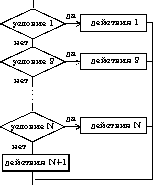

Примеры структуры ветвление

Школьный алгоритмический язык	Язык блок–схем
если x > 0 то y := sin(x) все
если a > b то a := 2*a; b := 1 иначе b := 2*b все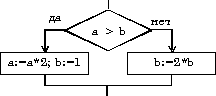
выборпри n = 1: y := sin(x) при n = 2: y := cos(x) при n = 3: y := 0 все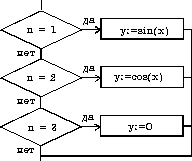
выборпри a > 5: i := i+1 при a = 0: j := j+1 иначе i := 10; j:=0 все

3. Базовая структура «цикл».Цикл– это неоднократное повторение каких–либо действий. Алгоритм, в котором есть структура «цикл» называется циклическим. Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла. Основные разновидности циклов представлены в таблице:

Школьный алгоритмический язык	Язык блок–схем
Цикл типа пока.
нц пока условие тело цикла (последовательность действий) кц Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.
Цикл типа для..
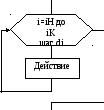
нц для i от i1 до i2 шаг k тело цикла (последовательность действий) кц Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне. Такой цикл называют циклом с параметром. Для организации цикла с параметром вводится величина (счетчик), которая меняет свое значение от начального до конечного с определенным шагом. Шаг равен разности между следующим и предыдущим значением величины. По умолчанию шал принимают равным единице.

Примеры структуры цикл

Школьный алгоритмический язык	Язык блок–схем
нцпока i кц
нц для i от 1 до 5 X[i] := i*i*i Y[i] := X[i]/2 кц

Цикл типа до

нц тело цикла условие кц Тело цикла размещается до проверки условия его окончания. Цикл выполнится хотя бы один раз.

Итерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия. На каждом шаге вычислений происходит последовательное приближение к искомому результату и проверка условия достижения последнего. Пример. Составить алгоритм вычисления бесконечной суммы 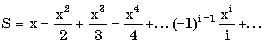с заданной точностью ε (для данной знакочередующейся бесконечной суммы требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше ε). Вычисление сумм – типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности. При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает. Решая эту задачу «в лоб» путем вычисления на каждом i-ом шаге частичной суммы S:=S + ((–1)**(i–1)) * (x**i) / i , мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р , то у следующего слагаемого числитель будет равен –р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m будет равно p/i , где i – номер слагаемого. Сравните эти два подхода по числу операций.

Алгоритм на школьном АЯ	Блок–схема алгоритма
алг Сумма (арг вещ x, Eps, рез вещ S) дано | 0 < x < 1 надо | S = x – x**2/2 + x**3/3 – . нач цел i, вещ m, p ввод x, Eps S := 0; i := 1 | начальные значения m := 1; p := –1 нц пока abs(m) > Eps p := –p*x | p – числитель | очередного слагаемого m := p/i | m – очередное слагаемое S := S + m | S – частичная сумма i := i + 1 | i – номер | очередного слагаемого кцвывод S кон

Алгоритм, в состав которого входит итерационный цикл, называется итеpационным алгоpитмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет «зацикливание» алгоритма, т.е. не будет выполняться основное свойство алгоритма – результативность. Вложенные циклы. Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной. При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла. Пример вложенных циклов «для» Вычислить сумму элементов заданной матрицы А(5,3).

Матрица А

S := 0; нц для i от 1 до 5 нц для j от 1 до 3 S:=S+A[i,j] кцкц

Пример вложенных циклов «пока» Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.

i:=2; P:=1 нцпока i нцпока j кц i:=i+2 кц

Алгоритм, который содержит несколько структур одновременно, называется комбинированным. Здесь представлен пример комбинированного алгоритма. При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм. Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы – компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем. Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке – программой для компьютера.

Источник

6.3 Базовые алгоритмические структуры

В теории программирования доказано, что для записи любого сколь угодно сложного алгоритма достаточно трёх базовых структур.

Линейная структура— все действия выполняются последовательно друг за другом (рис. 1). На практике редко удаётся представить схему алгоритма решения задачи в виде линейной структуры, так как задачи содержат различные условия или требуют многократного повторения вычислений.

Рис. 1. Линейная алгоритмическая структура.

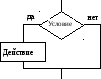
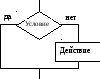
Разветвляющаяся структура— в зависимости от выполнения некоторого логического условия вычислительный процесс должен идти по одной или другой ветви (рис. 2). Условие — это логическое выражение, по которому происходит выбор направления выполнения алгоритма. В зависимости от значения логического выражения выполнение алгоритма идёт либо по левой, либо по правой ветви. Неполное ветвление применяется в тех случаях, если при выполнении одной из ветвей никаких изменений не происходит.

а)

Рис. 2. Разветвляющаяся алгоритмическая структура: а) полное ветвление, б) и в) неполное ветвление

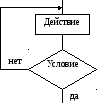
Циклическая структура содержит многократно выполняемые участки вычислительного процесса, называемые циклами (рис. 3). Использование циклов позволяет существенно сократить схему алгоритма. Различают циклы с заданным и неизвестным числом повторений, характеризующиеся последовательным приближением к исходному значению с заданной точностью.

Цикл с постусловием (с последующим условием) (рис. 3, а) служит для организации циклов с заранее неизвестным числом повторений. Цикл данного типа всегда выполняется, по крайней мере, один раз, так как проверка условия завершения цикла производится после выполнения тела цикла (блока «Действие»). Такой цикл называют ещё структурой с условием завершения цикла.

Цикл с предусловием(с предыдущим условием) (рис. 3, б) служит для организации циклов с заранее неизвестным числом повторений. Однако в отличие от цикла с последующим условием может не выполнится ни разу.

Цикл с параметром(рис. 3, в) используется для организации циклического повторения некоторого фрагмента программы в случаях, когда известно число повторений тела цикла.

б)

Рис. 3. Циклическая алгоритмическая структура: а) цикл с постусловием, б) цикл с предусловием, в) цикл с параметром

6.4 Примеры составления алгоритмов

6.4.1 Алгоритмы линейной структуры

Математическая формулировка задачи.

Определить площадь треугольника по формуле Герона

где a, b, c — длины сторон треугольника;

—полупериметр треугольника.

Описательный алгоритм решения задачи.

1. Ввод с клавиатуры исходных данных a,b,c.
2. Вычисление p по формуле.
3. Вычисление s по формуле .
4. Вывод результата s на экран монитора.

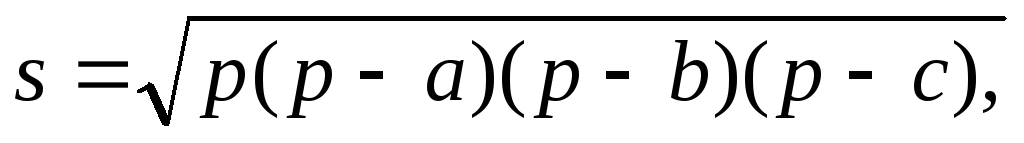
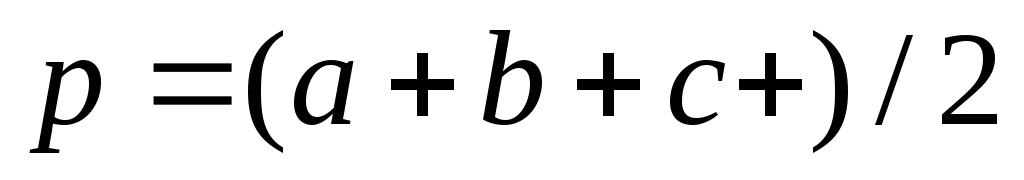
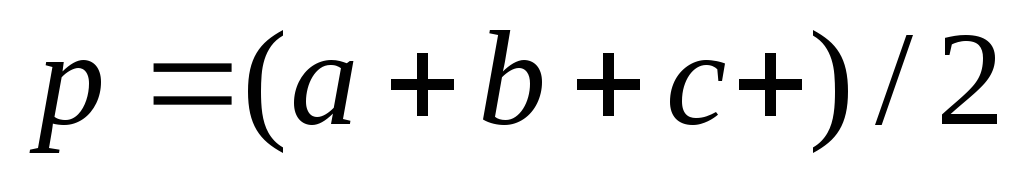Графический алгоритм решения задачи. Блок-схема алгоритма представлена на рисунке 1. На семе блоки расположены в той последовательности, в которой они должны выполняться Любая перестановка блоков приведёт к невозможности решения задачи. Рис. 4. Блок-схема алгоритма вычисления площади треугольника по формуле Герона.

Источник