Модель солнечной системы
Моделирование солнечной системы из 3-х планет
Написал прогу. Смысл её, это моделирование солнечной системы из 3-х планет.Вот код.. Собственно.
3D модель солнечной системы
Есть ли какие-то туториалы или справочная инфа по тому, как создать на java 3d модель солнечной.
Модель солнечной системы
Помогите пожалуйста как заставить планеты вращаться
Модель солнечной системы
Простой код, имитирующий движение планет солнечной системы. CLS SCREEN 12 WINDOW (0, 300)-(300.
Я думаю это нужно делать в потоке.
1) Описать класс Планеты, с полями размеров и скорости вращения и углом вращения
2) Описать метод вращения планеты вокруг солнца, которые принимает в аргументы экземпляр с полями из 1 пункта
3) Создать массив потоков(1 поток — 1 планета) и запустить их методом из 2 пункта. (Можно наверное и 1 потоком обойтись и в цикле каждым шагом перемещать все планеты)
Но если что умные люди меня поправят))
Добавлено через 26 минут
Класс планеты:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
public сlass Planet { public string Name; public int Radius; public double Alpha; public int Pos_X=0; public int Pos_Y=0; public int Centr_X=0; public int Centr_Y=0; public Planet(string a, int b, double c) { Name=a; Radius=b; Alpha=c; } }
public void DrawPlanet(ref Planet obj) { //здесь уже рисовать Планету //Рассчитывать следующие координаты для рисования }
Добавлено через 8 минут
Ах да, еще ось Z добавить надо, если 3D хотите, чтобы планета пряталась за солнцем или перекрывала её и другие планеты.
Получился какой то код но планеты крутятся одинаково хотя значения таймеров меняю, где здесь может быть ошибка?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows.Forms; namespace WindowsFormsApplication9 { public partial class Form1 : Form { public Form1() { InitializeComponent(); this.Load += Form1_Load; this.Paint += Form1_Paint; DoubleBuffered = true; } int r = 100; //радиус int x0 = 400; //координата X центра окружности int y0 = 300; //координата X центра окружности int q = 150; int w0 = 400; int e0 = 300; float x = 0, y = 0, z=0,c=0; double fi = 0.0; double fii = 0.0; void Form1_Load(object sender, EventArgs e) { Timer tmr = new Timer(); tmr.Interval = 10; tmr.Tick += tmr_Tick; tmr.Start(); Timer tmr2 = new Timer(); tmr2.Interval = 500; tmr2.Tick += tmr2_Tick; tmr2.Start(); } void tmr_Tick(object sender, EventArgs e) { fi += 0.01; if (fi > 2 * Math.PI) fi = 0.0; x = (float)(r * Math.Cos(fi) + x0); y = (float)(r * Math.Sin(fi) + y0); Invalidate(); } void tmr2_Tick(object sender, EventArgs e) { fii += 0.01; if (fii > 2 * Math.PI) fii = 0.0; z = (float)(q * Math.Cos(fi) + w0); c = (float)(q * Math.Sin(fi) + e0); Invalidate(); } void Form1_Paint(object sender, PaintEventArgs e) { e.Graphics.FillEllipse(Brushes.Yellow, x, y, 40, 40); e.Graphics.FillEllipse(Brushes.Blue, z, c, 60, 60); } private void timer1_Tick(object sender, EventArgs e) { } } }
Добавлено через 49 минут
Нашел ошибку, допустил синтаксическую ошибку связанную с «pi», надо было написать «pii»
Создаем симулятор солнечной системы
Предисловие
Вечная тяга к новому подтолкнула к изучению такого замечательного языка программирования, как Питон. Как это часто бывает, отсутствие идеи, на реализацию которой не жалко потратить свое время, сильно тормозило процесс.
Волею судьбы на глаза попался замечательный цикл статей о создании игры-платформера на Питоне
тут и тут.
Я решил взяться за один старый проект. За симулятор движения тел под действием сил гравитации.
Что из этого вышло читайте дальше.
Часть первая. Теоритическая
Чтобы решить задачу, нужно сначала четко себе ее представить.
Предположим, всеми правдами и неправдами нам удалось заполучить двумерный участок безвоздушного пространства с находящимися в нем телами. Все тела перемещаются под действием сил гравитации. Внешнего воздействия нет.
Нужно построить процесс их движения относительно друг друга. Простота реализации и красочность конечного результата послужат стимулом и наградой. Освоение Питона будет хорошей инвестицией в будущее.
Пускай наша система состоит из двух тел:
1. массивной звезды массой М и центром (x0, y0)
2. легкой планеты массой m, с центром в точке (x, y), скоростью v = (vx, vy) и ускорением a = (ax, ay).
Когда нам удастся разобрать этот случай, мы легко перейдем к сложным системам со взаимным влиянием звезд и планет друг на друга. Сейчас же речь пойдет о самом простом.
После несложных манипуляций со вторым законом Ньютона, законом всемирного тяготения и подобными треугольниками, я нашел, что:
ax = G * M * (x0-x) / r^3
ay = G * M * (y0-y) / r^3
Это позволяет составить алгоритм перемещения планеты в поле гравитации звезды:
1. Перед началом задаем начальное положение планеты (x, y) и начальную скорость (vx, vy)
2. На каждом шаге вычисляем новое ускорение по формуле выше, после этого пересчитываем скорость и координаты:
vx := vx + T * ax
vy := vy + T * ax
Осталось разобраться с константами G и T. Положим G = 1. Для нашей задачи это не так важно. Параметр T влияет на точность и скорость вычислений. Тоже положим 1 для начала.
Часть вторая. Практическая
Итак, моя первая программа на Питоне. При этом еще раз хочется поблагодарить Velese за практическое руководство.
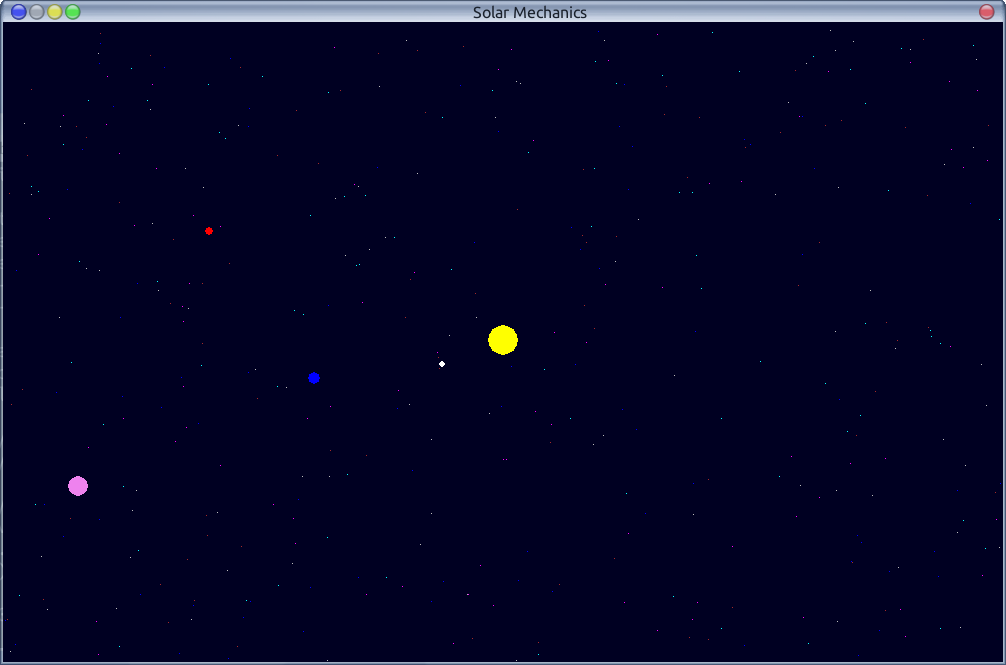
import pygame, math from pygame import * from math import * WIN_WIDTH = 800 WIN_HEIGHT = 640 PLANET_WIDTH = 20 PLANET_HEIGHT = 20 DISPLAY = (WIN_WIDTH, WIN_HEIGHT) SPACE_COLOR = "#000022" SUN_COLOR = "yellow" PLANET_COLOR = "blue" #Sun position X0 = WIN_WIDTH // 2 Y0 = WIN_HEIGHT // 2 #Sun mass M0 = 5000 #Stop conditions CRASH_DIST = 10 OUT_DIST = 1000 def main(): #PyGame init pygame.init() screen = pygame.display.set_mode(DISPLAY) pygame.display.set_caption("Solar Mechanics v0.1") #Space init bg = Surface((WIN_WIDTH,WIN_HEIGHT)) bg.fill(Color(SPACE_COLOR)) draw.circle (bg, Color(SUN_COLOR), (X0, Y0), 10) #Timer init timer = pygame.time.Clock() #Planet init planet = Surface((PLANET_WIDTH, PLANET_HEIGHT)) planet.fill(Color(SPACE_COLOR)) draw.circle (planet, Color(PLANET_COLOR), (PLANET_WIDTH // 2, PLANET_HEIGHT // 2), 5) #Planet to Sun distance r = 0.0 #Initial planet pos, speed and accel x = 100.0 y = 290.0 vx = 0.1 vy = 1.5 ax = 0.0 ay = 0.0 done = False while not done: timer.tick(50) for e in pygame.event.get(): if e.type == QUIT: done = True break r = sqrt((x - X0)**2 + (y - Y0)**2) ax = M0 * (X0 - x) / r**3 ay = M0 * (Y0 - y) / r**3 #New spped based on accel vx += ax vy += ay #New pos based on speed x += vx y += vy screen.blit(bg, (0, 0)) screen.blit(planet, (int(x), int(y))) pygame.display.update() if r < CRASH_DIST: done = True print("Crashed") break if r >OUT_DIST: done = True print("Out of system") break #Farewell print (":-)") if __name__ == "__main__": main() Так выглядит наша система после некоторого времени симуляции
Пока писалась эта заметка, симулятор разросся новой функциональностью: количество объектов в звездной системе не ограничевается, учитывается взаимное их влияние друг на друга, расчетная часть вынесена в свой класс, конфигурация системы задается в отдельном файле и добавлена возможность выбора систем.
Сейчас я занимаюсь поиском интересных сценариев системы и небольшими улучшениями интерфейса.
Вот пример того, что на данный момент в разработке:
Если эта заметка встретит положительные отзывы, обещаю продолжить рассказ о более новой версии.
1. Я благодарен всем комментаторам за критические замечания. Они дают большую пищу для размышлений.
2. Проект вырос. Все тела уже независимы, влияют друг на труга в соответствии с законом всемирного тяготения.Подсчитывается N^2 взаиможействий.
Сейчас есть возможность хранить конфигурации звездной системы во внешних файлах и выбирать на старте
Код тут
Запускать так: python3.3 main.py -f .ini
Различные конфигурации — там же.
3. Благодаря комментариям удалось найти и устранить главную недоработку — метод вычисления координат.
Сейчас используется метод Рунге-Кутты. По мере прочтения «Нежестких задач» буду осваивть новые методы.