Лабораторная работа № 2 Решение задач линейного программирования симплекс-методом
Программа для решения задач линейного программирования симплекс-методом. Имеется три режима решения задач:
В первом режиме программа сама выбирает разрешающий столбец и строку, которые обеспечивают максимальное возрастание или уменьшение целевой функции. А также автоматически пересчитывает все таблицы.
В пошаговом режиме, каждая пересчитанная таблица выводится на экран. Этот режим удобен для просмотра промежуточных результатов решения задачи. Разрешающий столбец и строку, в данном режиме, программа также выбирает сама.
В ручном режиме пользователь сам выбирает разрешающую строку и столбец.
Также есть возможность экспорта всех таблиц, полученных в ходе решения задачи, в Excel.
2) Интерфейс программы
Правило заполнения таблицы:
В первый столбец “b” вносятся свободные члены ограничений и целевой функции. В последнюю строку вносятся коэффициенты при целевой функции. В остальные ячейки вносятся коэффициенты при ограничениях.
Образец выполнения лабораторной работы
Пример задачи на максимизацию
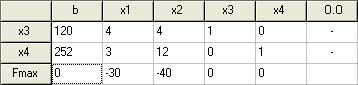
Завод выпускает продукцию 1-го и 2-го типа. Прибыль от реализации единицы продукции соответственно составляет 30 и 40 у.е. На выпуск единицы продукции 1-го типа расходуется 4 единиц сырья категории А, 4 ед. – категории В. Для выпуска единицы продукции 2-го типа расходуется сырья категории А — 3 ед., категории С – 12 единицы. Имеющиеся в наличие запасы сырья категории А – 120 единиц, В – 252 единицы.
Тип выпускаемой продукции
Прибыль от реализации единицы продукции (у.е.)
Необходимо определить количество продукции, при выпуске которой прибыль является максимальной.
Предположим, что будет изготовлено x1 единиц продукции 1-го типа, х2 – 2-го типа. Тогда для производства такого количества изделий потребуется затратить
Так как запас сырья данного вида не может превышать 7, то должно выполняться неравенство
Аналогичные рассуждения относительно возможного использования сырья вида B приведут к следующим неравенствам:
При этом так как количество выпускаемой продукции не может быть отрицательной, то
Далее, если будет выпущено х1 единиц продукции 1-го типа, х2 единиц продукции 2-го типа, то прибыль от их реализации составит
Таким образом, приходим к следующей математической задаче: дана система
трёх линейных неравенств с двумя неизвестными хj (j=1..2) и линейная функция относительно этих же переменных
требуется среди всех неотрицательных решений системы неравенств (2) найти такое, при котором функция (3) принимает максимальное значение.
Линейная функция (3), максимум которой требуется определить, вместе с системой неравенств (2) и условием неотрицательности переменных (1) образуют математическую модель исходной задачи.
Так как функция (3) линейная, а система (2) содержит только линейные неравенства, то задача (1)-(3) является задачей линейного программирования.
Заполняем симплекс-таблицу следующим образом:
Если задача на максимизацию, то меняются знаки при целевой функции:
Если задача на минимизацию, то меняются знаки при ограничениях:
В ячейки базисных переменных всегда вписывается единичная матрица. На пересечении строки с коэффициентами целевой функции и столбцов с базисными переменными всегда вписываются нули.
В ходе решения были получена следующая таблица:
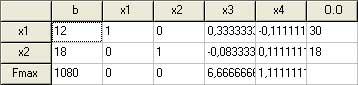
Базисным переменным x1, x2 – присваиваем значения свободных членов. Остальным переменным присваиваем нули.
Значение целевой функции показывается, в левом нижнем углу таблицы.
Таким образом, если предприятие изготовит 12 единиц изделий вида А и 18 единиц изделий В, то оно получит максимальную прибыль, равную: F=30*12 + 40*18 = 1080.
В соответствии с образцом выполнения работы составить экономико-математическую модель задачи линейного программирования. Затем, используя программу SCalc v1.6, решить задачу линейного программирования в трех режимах. Экспортировать все таблицы, полученные в ходе решения задачи, в Excel.
Сделать экономический анализ оптимального плана.
Результаты оформить в двух файлах следующим образом: первый – экономико-математическая модель задачи линейного программирования – должен быть выполнен в текстовом редакторе WORD, второй файл – решение данной задачи в табличном процессоре EXCEL.
Номер варианта заданий соответствует списочному номеру студента
Симплексный метод решения ЗЛП
Симплекс-метод — это итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения, улучшающих значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения.
- в виде симплексной таблицы (метод жордановых преобразований); базовой форме записи;
- модифицированным симплекс-методом; в столбцовой форме; в строчечной форме.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
- Также решают
Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word и Excel . При этом ограничения типа xi≥0 не учитывайте. Если в задании для некоторых xi отсутствуют ограничения, то ЗЛП необходимо привести к КЗЛП, или воспользоваться этим сервисом. При решении автоматически определяется использование М-метода (симплекс-метод с искусственным базисом) и двухэтапного симплекс-метода.
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X) зависит от количества реализованных партий товара Х и представлен в таблице.
| Объем товара Х (в партиях) | Доход G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
- Составление первого опорного плана. Переход к канонической форме задачи линейного программирования путем введения неотрицательных дополнительных балансовых переменных.
- Проверка плана на оптимальность. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить.
- Определение ведущих столбца и строки. Из отрицательных коэффициентов индексной строки выбирается наибольший по абсолютной величине. Затем элементы столбца свободных членов симплексной таблицы делит на элементы того же знака ведущего столбца.
- Построение нового опорного плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана—Гаусса.
Аналитическое введение в симплекс-метод
Симплексный метод является универсальным методом линейного программирования. Итак, если мы решаем ЗЛП в канонической форме, то система ограничений — это обычная система линейных уравнений. При решении задач ЛП получаются системы линейных уравнений, имеющие, как правило, бесконечно много решений. Например, пусть дана система
Здесь число уравнений равно 2, а неизвестных — 3, уравнений меньше. Выразим x1 и x2 через x3 :
Это общее решение системы. если переменной x3 придавать произвольные числовые значения, то будем находить частные решения системы. Например, x3=1 → x1=1 → x2=6. Имеем (1, 6, 1) — частное решение. Пусть x3=2 → x1=-3, x2= 1, (-3, 1, 2) — другое частное решение. Таких частных решений бесконечно много. Переменные x1 и x2 называются базисными, а переменная x3 — не базисная, свободная. Совокупность переменных x1 и x2 образует базис: Б (x1, x2). Если x3 = 0, то полученное частное решение (5, 11, 0) называется базисным решением, соответствующим базису Б (x1, x2). Базисным называется решение, соответствующее нулевым значениям свободных переменных.
В качестве базисных можно было взять и другие переменные: (x1, x3) или (x2, x3).
Как переходить от одного базиса Б(x1, x2) к другому базису Б(x1, x3)?
Для этого надо переменную x3 перевести в базисные, а x2 — в небазисные т. е. в уравнениях надо x3 выразить через x2 и подставить в 1-е: Базисное решение, соответствующее базису Б (x1, x3), таково: (-19/5; 0; 11/5). Если теперь от базиса Б (x1, x3) нам захочется перейти к базису Б (x2, x3), то
Базисное решение, соответствующее базису Б (x2, x3): (0;19/4; 7/8).
Из трех найденных базисных решений решение, соответствующее базису Б (x1, x3) — отрицательное x1 < 0, нас в ЗЛП интересуют только неотрицательные решения. Если задача ЛП имеет решение, то оно достигается на множестве базисных неотрицательных решений системы ограничений канонической формы. Поэтому идея симплекс-метода и состоит в последовательном переходе от одного базиса к другому, лучшему с точки зрения значения целевой функции. Пример . Решить задачу ЛП. Функцию F= x2 — x1 → min необходимо минимизировать при заданной системе ограничений:
-2x1 + x2 + x3 = 2
x1 + x2 + x5 = 5
x1 — 2x2 + x4 = 12
xi ≥ 0, i = 1, 5 Эти ограничения могут рассматриваться как произошедшие из неравенств, а переменные x3, x5, x4 — как дополнительные.
Запишем ограничения, выбрав базис из переменных Б< x3, , x4, x5>: Этому базису соответствует базисное неотрицательное решение
x1 = 0, x2 = 0, x3 = 2, x4 = 2, x5 = 5 или (0, 0, 2, 2, 5).
Теперь нужно выразить F через небазисные переменные, в нашем случае это уже сделано: F= x2 — x1.
Проверим, достигла ли функция F своего минимального значения. Для этого базисного решения F= 0 — 0 = 0 — значение функции равно 0. Но его можно уменьшить, если x1 будет возрастать, т. к. коэффициент в функции при x1 отрицателен. Однако при увеличении x1 значения переменных x4, x5 уменьшаются (смотрите второе и третье равенство системы ограничений). Переменная x1 не может быть увеличена больше чем до 2, иначе x4 станет отрицательной (ввиду равенства 2), и не больше, чем до 5, иначе x5 — отрицателен. Итак, из анализа равенств следует, что переменную x1 можно увеличить до 2, при этом значение функции уменьшится.
Перейдем к новому базису Б2, введя переменную x1 в базис вместо x4.
Б2x1, x3, x5>.
Выразим эти базисные переменные через небазисные. Для этого сначала выразим x1 из второго уравнения и подставим в остальные, в том числе и в функцию. Имеем:
F = -2 — x2 + x4.
Базисное решение, соответствующее базису Б2x1, x3, x5>, имеет вид (2, 0, 6, 0, 3), и функция принимает значение F= -2 в этом базисе.
Значение функции можно и дальше уменьшать, увеличивая x2. Однако, глядя на систему, x2 можно увеличивать лишь до 1, т. к. иначе из последнего равенства x5 = 3 — 3x2 + x4 следует, что при x2 > 1 x5 станет отрицательной. А у нас все переменные в ЗЛП предполагаются неотрицательными. Остальные уравнения системы не дают ограничений на x2. Поэтому увеличим x2 до 1, введя его в базис вместо x5: Б3x1, x2, x3>.
Выразим x2 через x5 и подставим во все уравнения:
Базисное решение, соответствующее базису Б3х1, х2, х3>, выписывается (4, 1, 9, 0, 0), и функция принимает значение F= -3. Заметим, что значение F уменьшилось, т. е. улучшилось по сравнению с предыдущим базисом.
Посмотрев на вид целевой функции , заметим, что улучшить, т. е. уменьшить значение F нельзя и только при x4 = 0, x5 = 0 значение F= -3. как только x4, x5 станут положительными, значение F только увеличится, т. к. коэффициенты при x4, x5 положительны. Значит, функция F достигла своего оптимального значения F* = -3. Итак, наименьшее значение F, равное -3, достигается при x1* = 4, x2* = 1, x3* = 9, x4* = 0, x5* = 0. На этом примере очень наглядно продемонстрирована идея метода: постепенно переходя от базиса к базису, при этом всегда обращая внимание на значения целевой функции, которые должны улучшиться, мы приходим к такому базису, в котором значение целевой функции улучшить нельзя, оно оптимально. Заметим, что базисов конечное число, поэтому количество шагов, совершаемых нами до того нужного базиса, конечно.