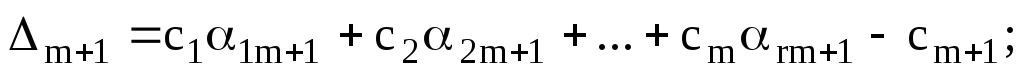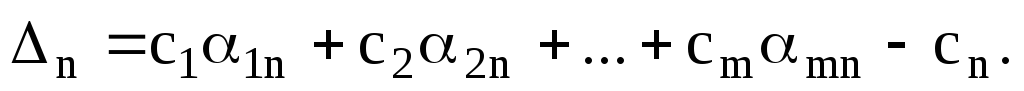- Симплексный метод решения задач линейного программирования
- 1) Построение начального опорного плана.
- 2) Составление симплексных таблиц. Критерий оптимальности.
- 2.3. Признак оптимальности опорного плана
- 2.4. Переход к нехудшему опорному плану
- 2.5. Симплексные преобразования
- 2.6. Признак оптимальности опорного плана. Симплексные таблицы
Симплексный метод решения задач линейного программирования
Симплексный метод – это метод последовательного улучшения плана. Этим методом можно решать задачи линейного программирования с любым количеством переменных и ограничений.
Этот метод включает в себя три основные этапа:
- Построение начального опорного плана.
- Правило перехода к лучшему (точнее, нехудшему) решению.
- Критерий проверки найденного решения на оптимальность.
1) Построение начального опорного плана.
Данную задачу линейного программирования необходимо сначала привести к каноническому виду; при этом правые части ограничений должны быть неотрицательными. Признаком возможности построения начального опорного плана служит наличие в каждом ограничении-равенстве с неотрицательной правой частью базисной переменной. Базисной называют плановую переменную, которая входит только в одно уравнение (а в другие не входит), и при этом имеет коэффициент, равный единице. Пусть задача линейного программирования приведена к каноническому виду, и все уравнения системы ограничений имеют свою базисную переменную. Приравняв базисные переменные к соответствующим правым частям ограничений, а остальные переменные к нулю, получим опорное или базисное решение задачи. Пример. Для данной задачи линейного программирования найти начальный опорный план (базисное решение). 


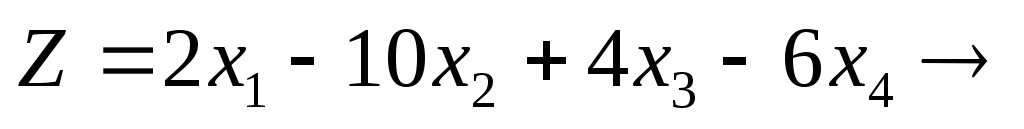
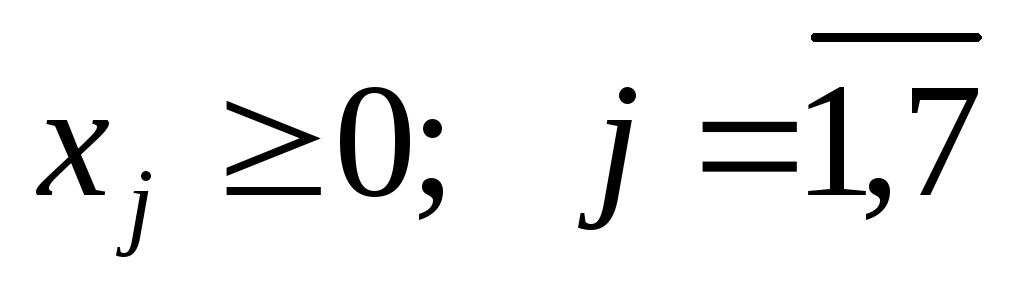




2) Составление симплексных таблиц. Критерий оптимальности.
Симплексный метод удобно применять, используя построение симплексных таблиц. Первая симплексная таблица, соответствующая начальному плану, имеет вид:
| Базис | 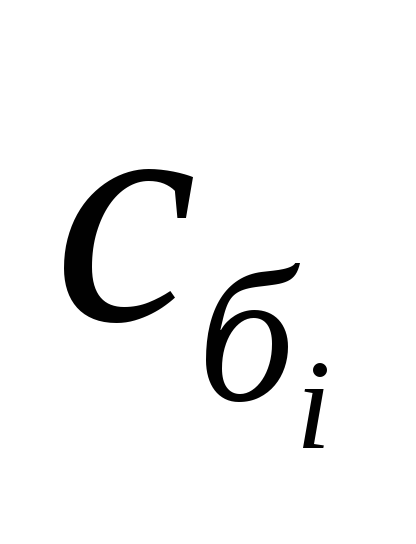 | В |  |  | … |  |  |
 | 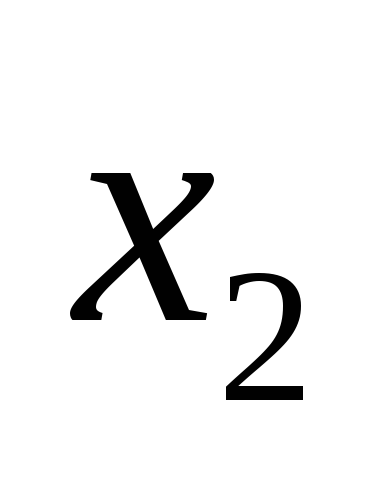 | … | 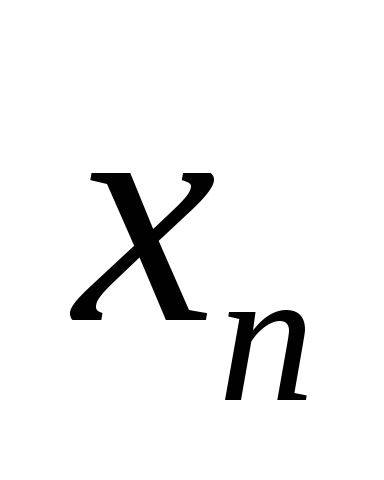 | ||||
 |  |  |  |  | … |  | |
 |  | 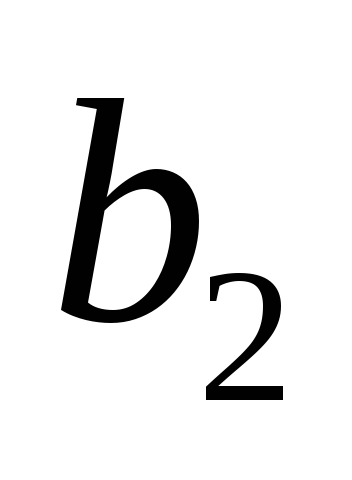 |  | 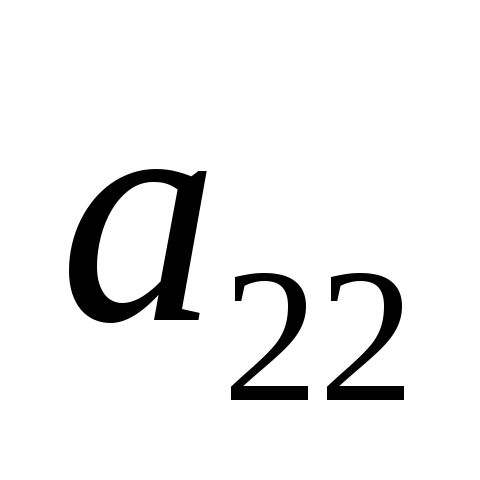 | … |  | |
| … | … | … | … | … | … | … | |
 | 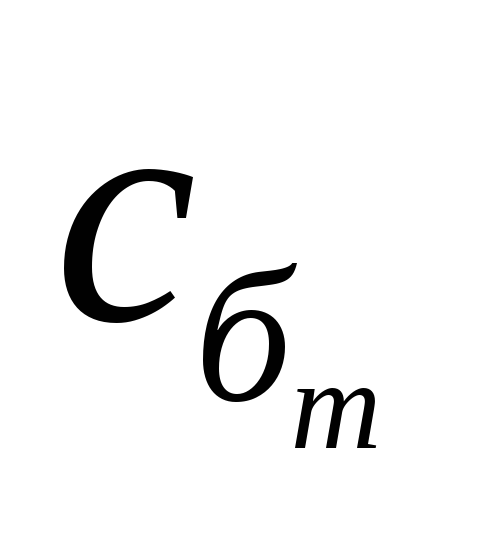 | 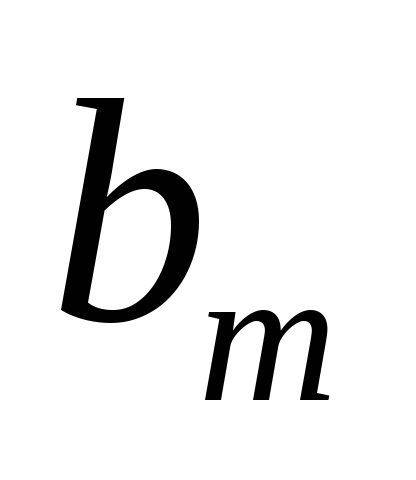 |  |  | … | 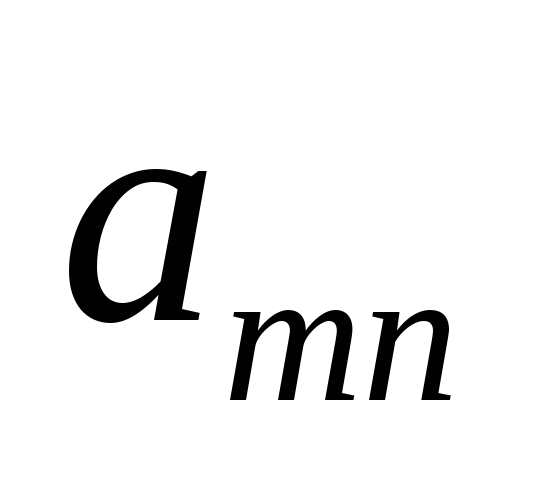 | |
 |  |  |  | … |  | ||
Здесь приняты следующие обозначения. Столбец «Базис» – это базисные переменные. Столбец «









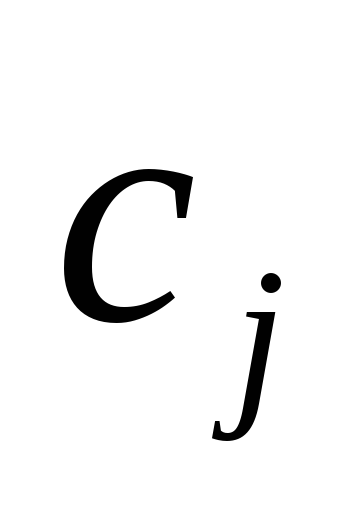










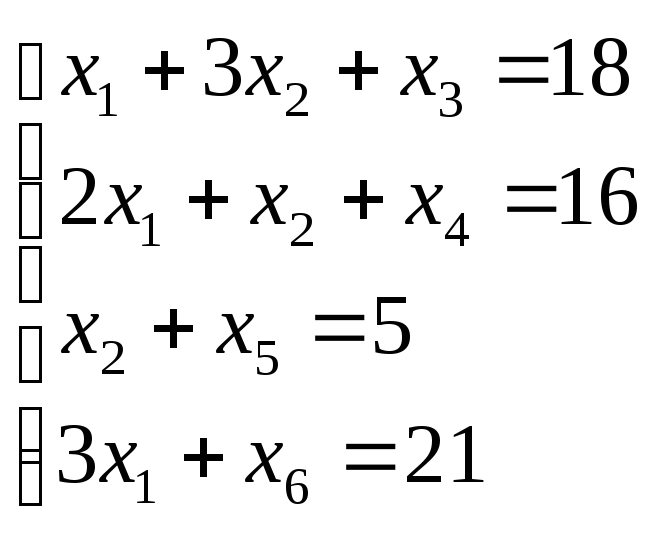



| Базис | 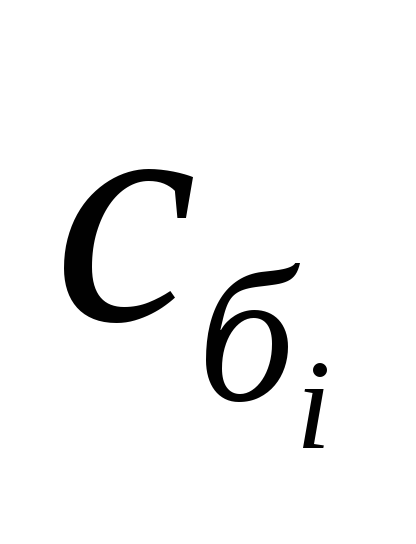 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 |  |  |  | 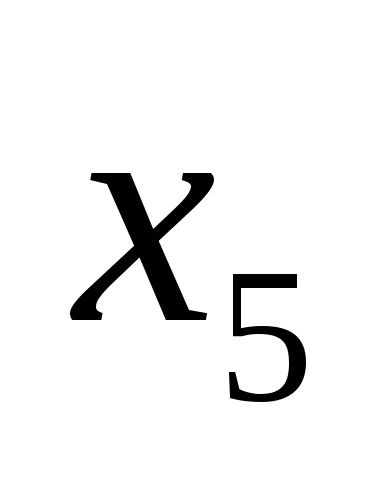 |  | ||||
 | 0 | 18 | 1 | 3 | 1 | 0 | 0 | 0 | 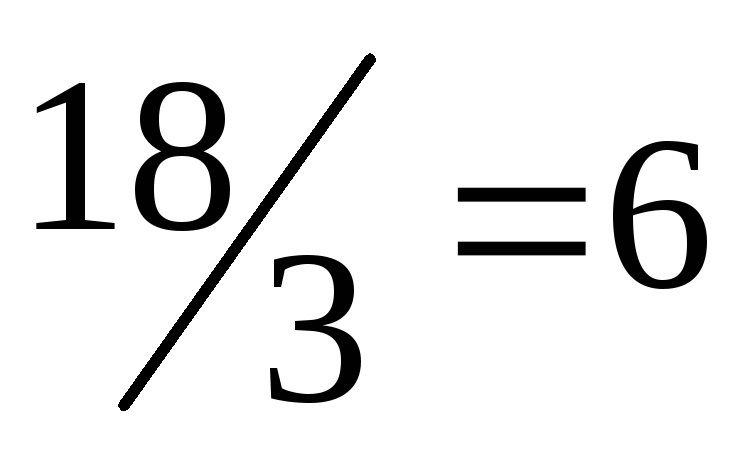 |
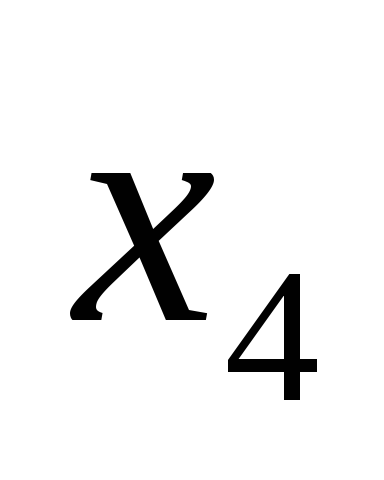 | 0 | 16 | 2 | 1 | 0 | 1 | 0 | 0 | 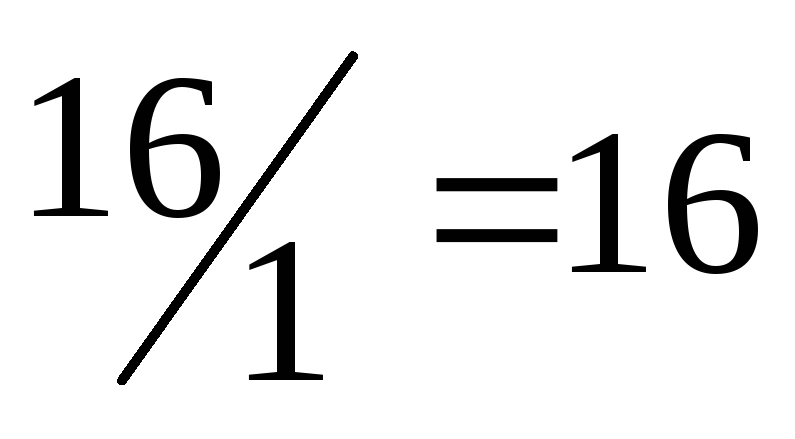 |
 | 0 | 5 | 0 | 1 | 0 | 0 | 1 | 0 |  |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | – |
 |  0 0 |  –2 –2 |  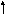 –3 –3 |  0 0 |  0 0 |  0 0 |  0 0 | ||
Здесь 






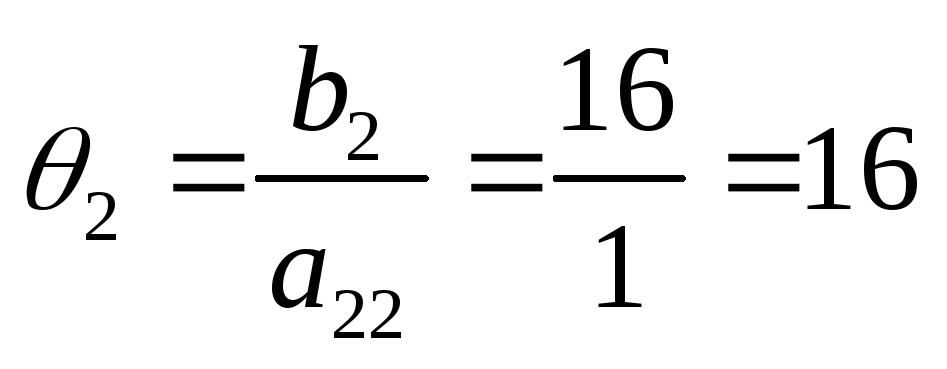

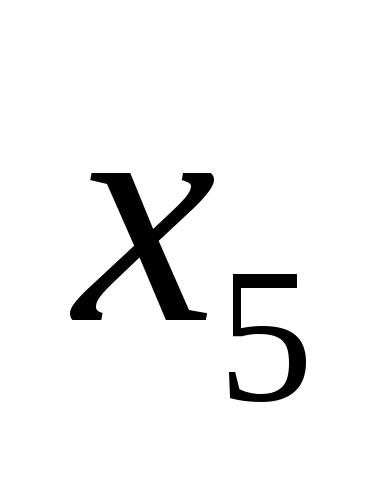
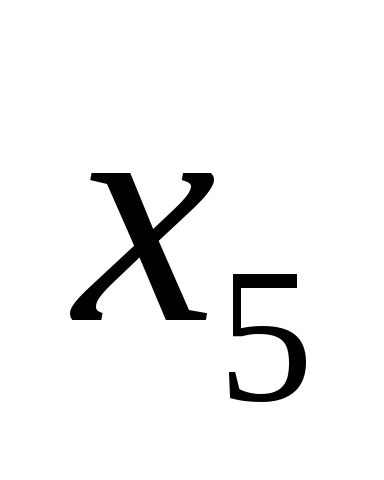

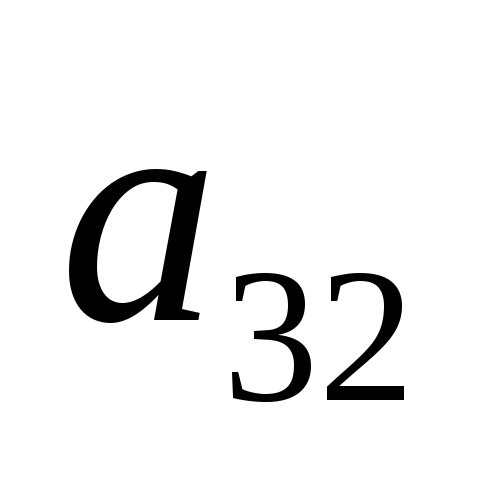
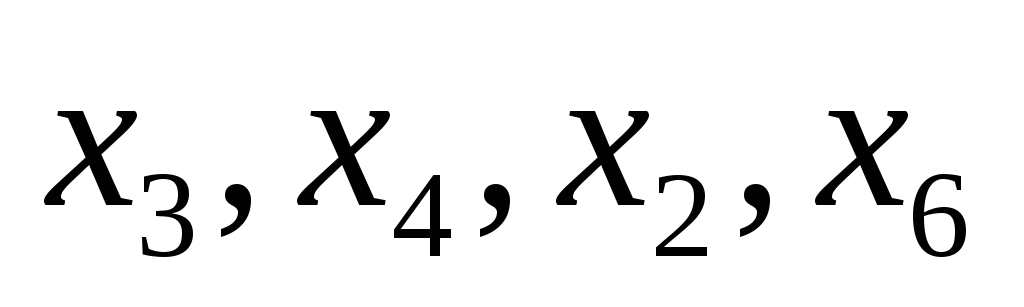




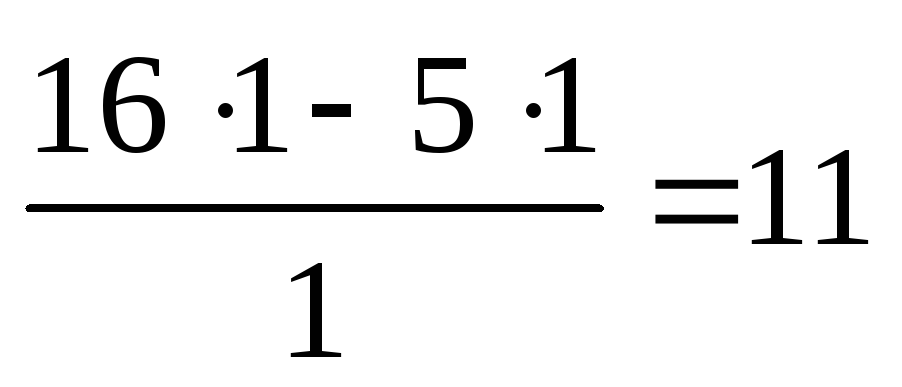



| Базис | 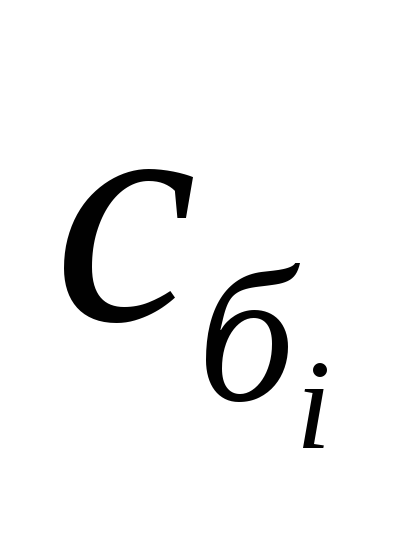 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 | 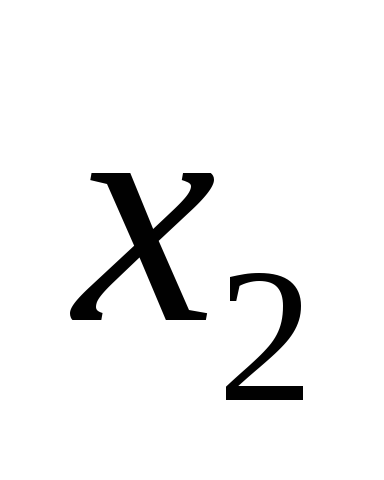 | 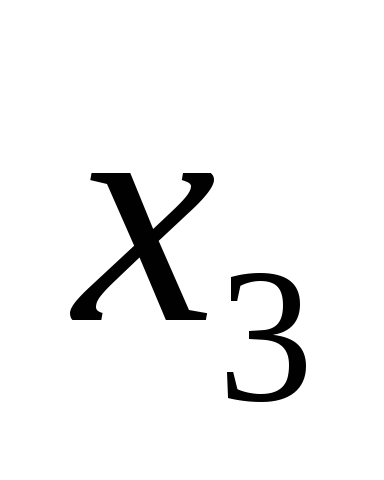 |  |  |  | ||||
 | 0 | 18 | 1 | 3 | 1 | 0 | 0 | 0 | 6 |
 | 0 | 16 | 2 | 1 | 0 | 1 | 0 | 0 | 16 |
 | 0 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5 |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | – |
 | 0 | –2 | –3 | 0 | 0 | 0 | 0 | таб. 1 | |
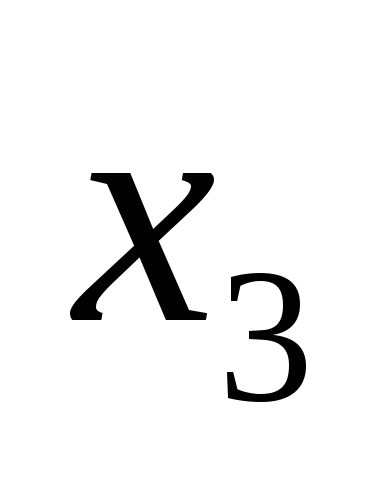 | 0 | 3 | 1 | 0 | 1 | 0 | –3 | 0 | 3 |
 | 0 | 11 | 2 | 0 | 0 | 1 | –1 | 0 | 5,5 |
 | 3 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | – |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | 7 |
 | 15 | –2 | 0 | 0 | 0 | 3 | 0 | таб. 2 | |
| Базис | 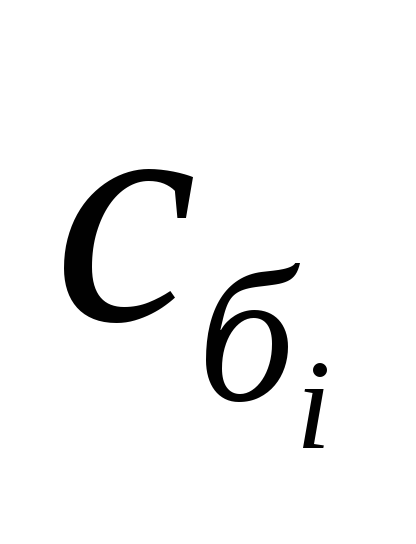 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 |  |  |  | 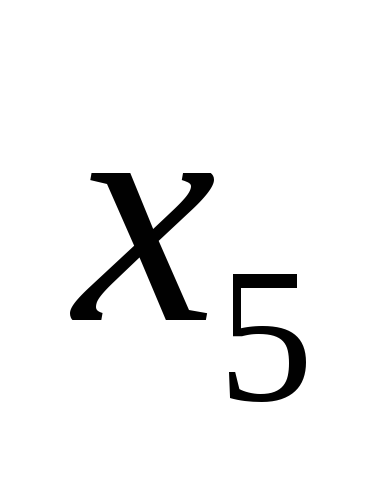 |  | ||||
 | 2 | 3 | 1 | 0 | 1 | 0 | –3 | 0 | – |
 | 0 | 5 | 0 | 0 | –2 | 1 | 5 | 0 | 1 |
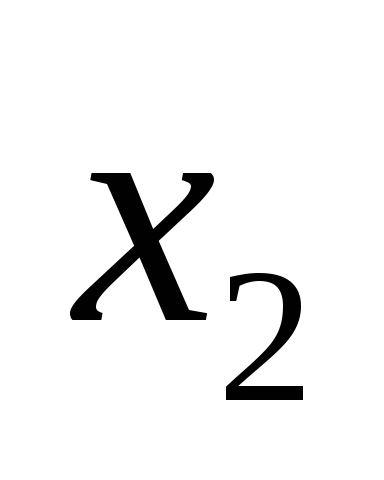  | 3 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5 |
 | 0 | 12 | 0 | 0 | –3 | 0 | 9 | 1 |  |
 | 21 | 0 | 0 | 2 | 0 | –3 | 0 | таб. 3 | |
 | 2 | 6 | 1 | 0 | –0,2 | 0,6 | 0 | 0 | |
 | 0 | 1 | 0 | 0 | –0,4 | 0,2 | 1 | 0 | |
 | 3 | 4 | 0 | 1 | 0,4 | –0,2 | 0 | 0 | |
 | 0 | 3 | 0 | 0 | 0,6 | –1,8 | 0 | 1 | |
 | 24 | 0 | 0 | 0,8 | 0,6 | 0 | 0 | таб. 4 | |
О













| а) | 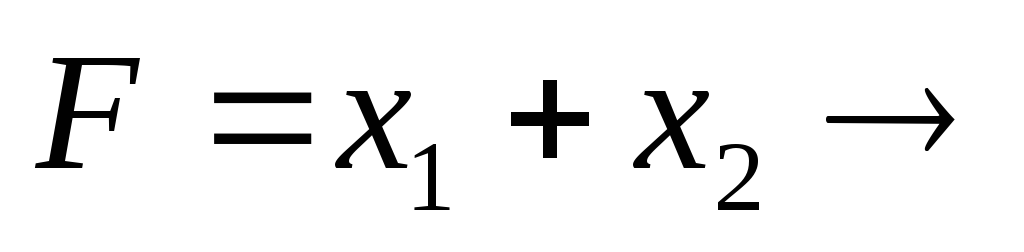 max max 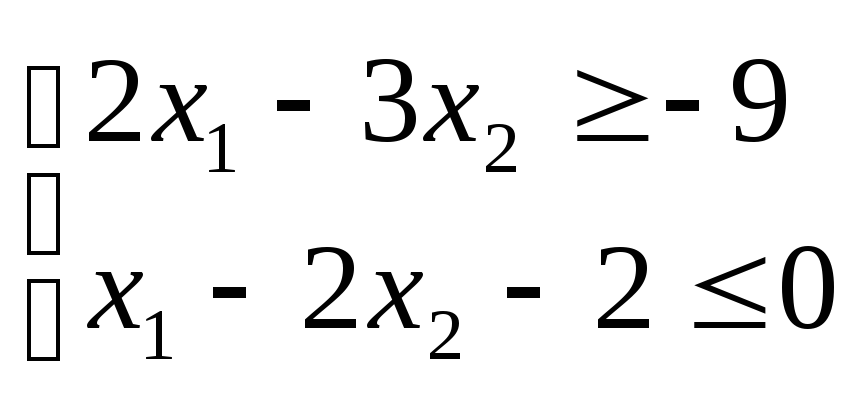 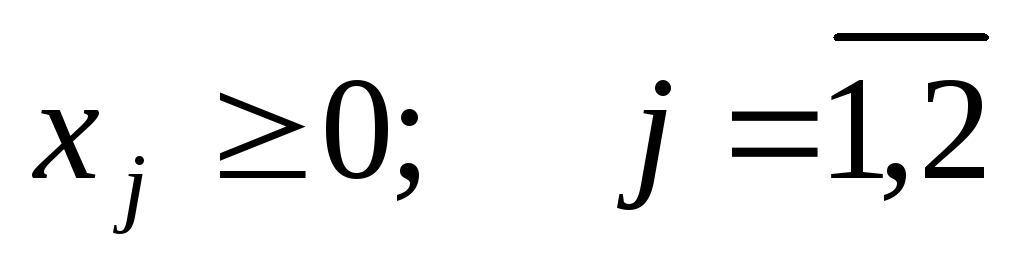 | б) |  min min   |
2.3. Признак оптимальности опорного плана
Теорема 1. Пусть исходная задача решается на максимум. Если для некоторого опорного плана все оценки неотрицательны, то такой планоптимален.
Теорема 2.Если исходная задача решается на минимум и для некоторого опорного плана все оценки неположительны, то такой планоптимален.
2.4. Переход к нехудшему опорному плану
Рассмотрим ЗЛП на максимум.Приведем ее к каноническому виду и занесем в симплексную таблицу.
Если все j0, то начальный опорный планx0оптимален.
С этой целью выбирают разрешающий элемент.
Выбор разрешающего столбца. Среди отрицательных оценок находят максимальную по абсолютной величине: .
Вектор-столбец 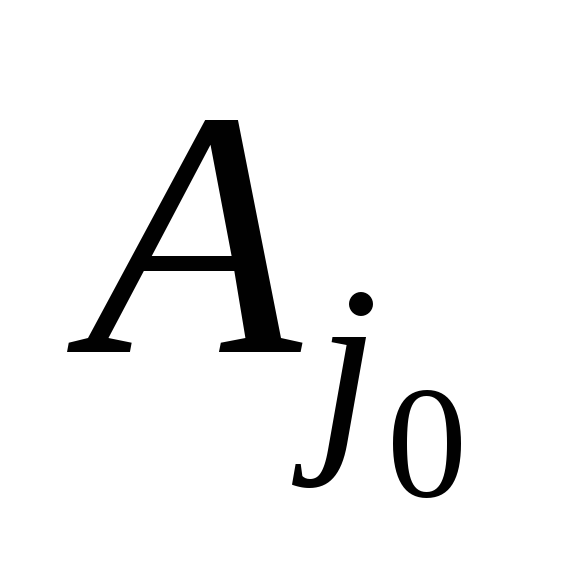

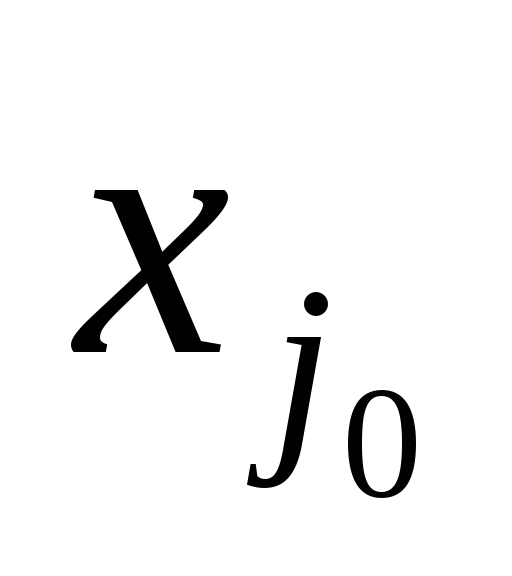
Замечание. Если задача решается на минимум, то разрешающий столбец выбирается из условия .
Выбор разрешающей строки. Находят отношения . Они называютсясимплексными.
Среди симплексных отношений определяют наименьшее, т. е.
.
Если это условие выполняется при нескольких i, то в качествеi0можно выбрать любое.
Оно и укажет строку, в которой содержится исключаемая из базиса переменная Строкаi0, соответствующая минимальному симплексному отношению, называетсяразрешающей.
Выбор разрешающего элемента.Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки будетразрешающим (илиключевым).
Переходим к новой таблице. Переменную 
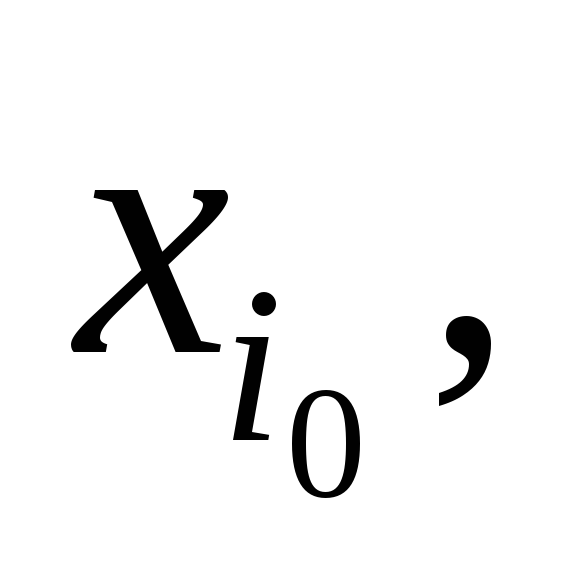
Замечание.Поскольку minz= –max (–z), задачу минимизации можно формально заменить задачей максимизации функции –z. Затем полученный максимум следует взять с противоположным знаком. Это и будет искомый минимум исходной ЗЛП.
2.5. Симплексные преобразования
Чтобы завершить шаг преобразований, ведущих к новому опорному плану, составляют таблицу по следующим правилам:
1. элементы строкиi0новой таблицы равны соответствующим элементам разрешающей строки старой таблицы, деленным на разрешающий элемент.
2. все элементы столбцаj0новой таблицы равны нулю, за исключением .
3. чтобы получить все остальные элементы (включая элементы индексной строки) новой таблицы, нужно воспользоватьсяправилом прямоугольника (рис. 6).
Для этого в прежней таблице выделяют прямоугольник, вершинами которого служат нужные для вычисления элементы. Диагональ, содержащую разрешающий 

.
Шаг симплексного метода, позволяющий перейти от одного опорного плана к другому, нехудшему, называется итерацией. Таким образом, симплексный метод являетсяитеративным методом последовательного улучшения плана.
2.6. Признак оптимальности опорного плана. Симплексные таблицы
Для того, чтобы было удобнее решать ЗЛП симплексным методом были придуманы симплексные таблицы, которые позволяют максимально алгоритмизировать процесс решения задачи линейного программирования. Симплексная таблица составляется только в том случае, если составлен начальный опорный план.
Пусть ЗЛП представлена в каноническом виде:
при
С помощью метода Гаусса (см. 1.12) преобразуем систему ограничений и приведем ее к следующему виду:
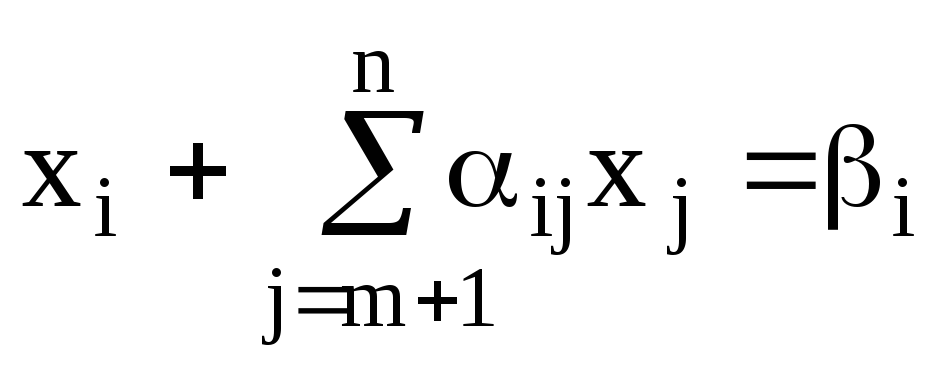

Из записи ЗЛП видно, что первые m переменных являются базисными. При этом мы не нарушаем общности рассуждений, так как то, что базисными будут первые m переменных, позволит более наглядно проиллюстрировать теорию.
Составим симплексную таблицу:
В первом столбце (БП) пишутся базисные переменные. Все базисные переменные пишутся В СООТВЕТСТВИИ С УРАВНЕНИЯМИ, ДЛЯ КОТОРЫХ ДАННЫЕ ПЕРЕМЕННЫЕ ЯВЛЯЮТСЯ ПРЕДПОЧТИТЕЛЬНЫМИ.
Во втором столбце (СБ) пишутся коэффициенты для соответственных базисных переменных в целевой функции.
В третьем столбце (А) пишутся свободные члены в уравнениях системы ограничений.
В первой строке после обозначения первых трех столбцов (БП, СБ, А) пишутся все переменные, которые есть в ограничениях, включая дополнительные и искусственные. Порядок следования переменных неизменен. под каждой переменной пишется ее коэффициент в целевой функции.
В таблице со второй строки четвертого столбца пишутся все коэффициенты соответственных переменных в системе ограничений.
В последней строке пишутся оценки. Оценки считаются по формулам (см. 1.12):
Оценки для базисных переменных равны 0.
Замечание: Оценки считаются как скалярное произведение соответственного столбца на столбец СБ минус коэффициент в целевой функции для данной переменной.
Последнюю строку называют индексной строкой симплексной таблицы. Значение – значением целевой функции для данного начального опорного плана, а все остальные Δ – оценками свободных переменных.
Теорема 1: (признак оптимальности опорного плана при решении задач на максимум) Пусть исходная ЗЛП решается на максимум. Если для некоторого опорного плана в индексной строке симплексной таблицы все оценки 

Теорема 2: (признак оптимальности опорного плана при решении задач на минимум) Пусть исходная ЗЛП решается на минимум. Если для некоторого опорного плана в индексной строке симплексной таблицы все оценки 

Пример 1: Составить симплексную таблицу и посчитать оценки для задачи линейного программирования вида:
Построение начального опорного плана рассмотрено в 2.5.
Базис системы составляют переменные: