Примеры решения задач линейного программирования геометрический метод

Геометрический метод решения задач линейного программирования

Если число переменных в общей задаче линейного программирования равно двум или трем, то такая задача имеет особенно простое геометрическое истолкование и, соответственно, ее решение может быть получено геометрическим методом. Для конкретности рассмотрим следующую задачу ЛП:

f(X) = c₁x₁ + c₂x₂ max

a₁₁x₁ + a₁₂x₂ b₁

a₂₁x₁ + a₂₂x₂ b₂

a_m1x₁ + a_m2x₂ b_m

x₁ 0, x₂ 0

Каждому из ограничений задачи (4) соответствует полуплоскость, а в совокупности они представляют на плоскости Ox₁x₂ многоугольник (или пустое множество). Геометрически, с учетом ограничений на знак переменных x₁ и x₂, имеем следующую картину:

Область допустимых решений (ОДР) – это область внутри шестиугольника ABCDEF. Фиксированным значениям целевой функции f(X) соответствует фиксированное положение прямой L (уравнение прямой L: c₁x₁ + c₂x₂ = d, где d фиксированное значение), возрастание f(X) соответствует движению прямой L в направлении, указанном стрелками. Когда прямая L занимает положение, соответствующее ее прохождению через точку C (точка C выделена жирно – это одна из вершин шестиугольника), целевая функция достигает своего наибольшего значения. Таким образом, решением задачи ЛП будет x₁ = x₁ c , x₂ = x₂ c , а f(X опт ) = f(X c ), где x₁ c , x₂ c – координаты точки C.

Пример. Решить следующую задачу линейного программирования:

Здесь для удобства студентов выбраны более привычные для них переменные x и y. Область допустимых решений изображена на Рис. 2:

Она представляет собой многоугольник ABCDEF (здесь уравнение прямой BC: y = 2, CD: x + 2y = 6, DE: x = 3, EF: y = 0, AF: x + y =1,AB: x = 0). Прямая L соответствует уравнению целевой функции: 2x + y = d, где d – параметр. Очевидно, что целевая функция будет достигать максимума в ОДР, когда прямая L будет проходить через точку D. Точка D это точка пересечения прямых CD и DE, решая совместно систему уравнений:

получим координаты точки D: x = 3, y = 3/2. Таким образом, решением данной задачи будет x = 3, y = 3/2, значение целевой функции при этом будет f(X опт ) = 4 + 3/2 = 11/2.

Программирования симплекс – методом

Каноническую задачу ЛП можно записать в виде таблицы:

Начальный базисный план задачи получается из этой таблицы и имеет вид вектора

X b = (0,0,…, 0,b₁,b₂, … ,b_r) т , то-есть x₁ b =0,x₂ b =0,…,x_k b =0,x_k+1 b =b₁,x_k+2 b =b₂, …,x_n b =b_r.

Описываемый ниже алгоритм решения канонической задачи ЛП основан на этой таблице.

Рассмотрим подробнее последний блок алгоритма о преобразовании таблиц. По условию, в этом случае в столбце таблицы, соответствующему положительному элементу c_p , есть положительные элементы a_ip ; для каждого из этих элементов находим отношение b_i/a_ip и находим наименьшее из этих отношений, пусть оно соответствует элементу a_kp, это означает, что таблицу нужно преобразовывать, переводя переменную x_k из базисных переменных в свободные переменные, а переменную x_p наоборот переводят из свободных переменных в базисные; делается это следующим образом: сначала преобразуется k –тая строка таблицы – путем деления всех элементов этой строки на a_kp — результаты заносятся в k – тую строку новой таблицы, затем по формулам метода Гаусса для систем линейных алгебраических уравнений преобразуются остальные элементы таблицы (табличный вариант этого метода носит название «правила двух перпендикуляров» и оно состоит в том, что элемент новой таблицы получается путем вычитания из соответствующего элемента старой таблицы произведения элементов, стоящих на концах перпендикуляров, проведенных от старого элемента на p – тый столбец и на уже полученную k — тую строку новой таблицы). Рассмотрим пример.

f(X)= — 3x₄ + 8x₅ + 2x₆ + 15 min

x₁ – 2x₄ + 3x₅ – 7x₆ = 12;

x₂ + 2x₄ + x₅ – 3x₆ = 8;

x₃ + x₄ + 4x₅ – 5x₆ = 7;

x_j 0; j = 1, 2, 3, 4, 5, 6.

Задача является канонической, переменные x₁, x₂, x₃ – базисные переменные, остальные переменные x₄, x₅, x₆ – свободные. Заполняем исходную симплекс – таблицу:

В строке для f(X) среди элементов c₁, c₂, …, c₆ есть только один положительный элемент c₄ = 3, а в столбце над этим элементом (столбец выделен жирным шрифтом) есть два положительных элемента (1 и 2). Вычисляем для этих двух элементов отношения b_i/a_ip, получаем 8/2 = 4, 7/1 = 7. Наименьшим из чисел 4 и 7 является 4, это число соответствует элементу a₂₄ =2, стоящем в строке таблицы, соответствующей базисной переменной x₂. Это означает, что переменная x₂ из базисных переменных перейдет в разряд свободных, а на ее место в разряд базисных придет переменная x₄, что и отражено в первом столбце следующей части таблицы. Преобразование таблицы начинается со старой строки для x₂: все элементы этой строки делятся на число a₂₄ =2 и результат заносится в строку для x₄ новой части таблицы (эта строка выделена жирным шрифтом). Дальнейшие преобразования таблицы осуществляются по правилу двух перпендикуляров (строка и столбец, на которые нужно опускать перпендикуляры, выделены жирным шрифтом). Например, первый элемент, стоящий в строке для x₁ (а там стоит число 12), получается по формуле 12 – 4(-2) = 20, потому что на концах перпендикуляров, опущенных из ячейки для числа 12 на выделенные жирным шрифтом строку и столбец, стоят числа 4 и (-2). Число 20 записывается в соответствующую ячейку новой части таблицы и так пересчитываются все остальные элементы старой части таблицы. После преобразования таблицы снова смотрим на строчку для f(X), среди элементов c_j этой строки есть положительный элемент c₆ = 5/2, а в столбце над этим элементом нет положительных элементов. В соответствии с алгоритмом, получаем, что задача не имеет решения в силу неограниченности целевой функции.

Для продолжения скачивания необходимо пройти капчу:

Источник

Решения X*

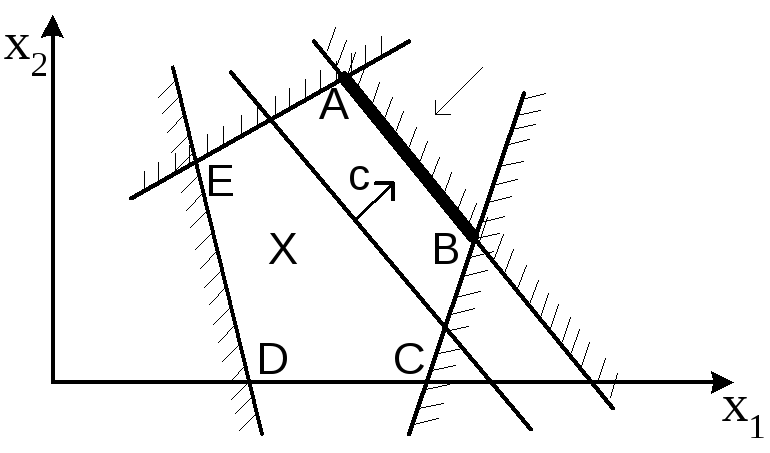
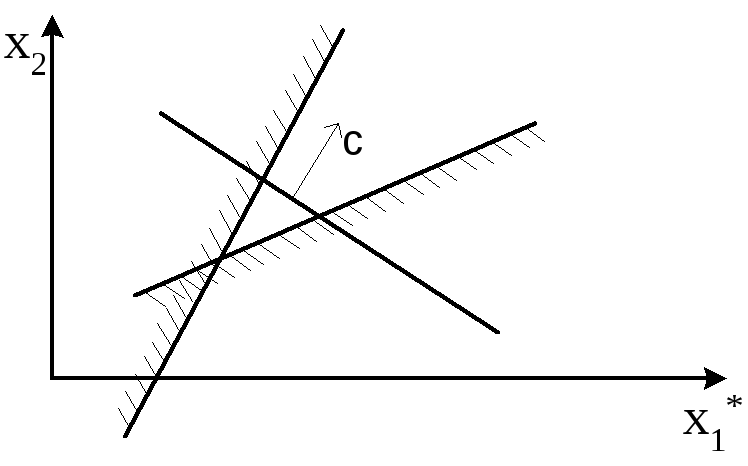
Во втором случае ЗЛП заведомо разрешима и имеет либо единственное решение (рис.1), совпадающее с одной из вершин допустимого многогранника X, либо бесконечное множество решений (рис.3) – ребро или грань многогранника, параллельные плоскостям семейства (3). Рис.3 Пример ЗЛП, имеющий бесконечное множество решений (ребро АВ многогранника допустимых решений ABCDE) Если допустимое множество решений ЗЛП неограниченно, ответ на вопрос о существовании ее решения для задачи максимизации зависит от того, ограничена сверху на этом множестве целевая функция zили нет. Если ограничена, задача разрешима, причем возможны те же ситуации, что и во втором из рассмотренных выше случаев. Если нет – решение отсутствует (рис.4). Для задачи минимизации, в случае неограниченного множества допустимых решенийX, ответ на вопрос о существовании решения ЗЛП Рис.4 Пример ЗЛП, имеющей неограниченное множество допустимых решений. зависит от того, ограничена снизу на множестве Xцелевая функцияzили нет. Возникающие ситуации те же что и у задач максимизации.

1. Геометрическое решение ЗЛП в стандартной форме.

Если задача линейного программирования в стандартной форме содержит всего лишь две переменные x₁ и x₂ (т.е. n=2), то ее можно решить следующим способом, основанным на ее геометрической интерпретации. Каждое неравенство системы ограничений и условие неотрицательности представляют собой полуплоскость. Пересечение полуплоскостей образует выпуклое многоугольное множество (многогранник допустимых решений). Целевая функция графически изображается множеством параллельных прямых, называемых линиями уровня, каждой из которых соответствует конкретное значение z. Для решения задачи линия уровня сдвигается в пределах области допустимых решений (многогранника допустимых решений) в направлении вектора-градиента grad z=f(x) = до самой крайней точки области для задачи максимизации , и в направлении антиградиента

• grad z=для задачи минимизации. Координаты этой

точки и определяют решение ЗЛП (оптимальный план задачи).

Пример 1 Решить геометрическим способом злп:

Z = 6x₁+2x₂  max 4x₁+5x₂  61 (a) -3x₁+4x₂  24 (б) 5x₁-3x₂  30 (в) x₁ 0, x₂ 0

Решение

Построим область допустимых решений ЗЛП, представляющую собой множество точек, удовлетворяющих ограничениям задачи. Область допустимых решений – ограниченный многоугольник, выделенный внешней (б) (в) Рис.5 Пример геометрического решения ЗЛП в стандартной форме при n=2. штриховкой. Вектор-градиент целевой функции grad z=c= определяет направление ее возрастания. Из рисунка видно, что целевая функция z принимает максимальное значение в точке пересечения прямых, задаваемых неравенствами (а) и (б): 4x₁+5x₂ = 61 5x₁-3x₂ = 30 Решив эту системы уравнений, получим x₁ * =9, x₂ * =5. Максимальное значение функции z_max=64. Пример 2 Решить геометрическим способом ЗЛП: Z = 8x₁+10x₂  max x₁+2x₂  220 (a) 2x₁+x₂  260 (б) 4x₁+5x₂  640 (в) x₁ 0, x₂ 0 Решение Построим область допустимых решений задачи. (б) (в) Р ис.6 Пример геометрического решения ЗЛП. Эта область предоставляет собой выпуклый многоугольник ОМ₁М₂М₃М₄. Определим координаты вершин многоугольника, как точки пересечения соответствующих прямых. Координаты вершины М₁ из решения системы x₁+2x₂=220 x₁=0 Решив эту систему, получим М₁=. Координаты вершины М₂= получим из системы x₁+2x₂=220 4x₁+5x₂=640 Координаты вершины М₃= получим из системы 2x₁+x₂=260 4x₁+5x₂=640 Координаты вершины М₄= получим из системы 2x₁+x₂=260 x₂=0 Из геометрической интерпретации ЗЛП видно, что, если задача имеет решение, то оно достигается в одной из вершин многоугольника допустимых решений. Поэтому для того, чтобы найти решение достаточно перебрать все вершины многоугольника допустимых решений. Вычислим значения целевой функции во всех вершинах этого многоугольника: z₀ = f(M₀) = 0, z₁ = f(M₁) = 1100, z₂ = f(M₂) = 1280, z₃ = f(M₃) = 1280, z₄ = f(M₄) = 1040. Отсюда видно, что целевая функция z достигает максимального значения в двух вершинах М₂ и М₃ , т.е. в своем крайнем положении линия уровня z = 8x₁+10x₂=const=1280 содержит вершины М₂, М₃ и, следовательно, все ребро (М₂ , М₃). Таким образом, решений бесконечно много – все точки ребра (М₂ , М₃). При этом максимальное значение целевой функции z равно 1280. Пример 3 Решить геометрическим способом ЗЛП z=x₁+x₂  max x₁+x₂  -1 (a) x₁  0, x₂  0

Источник

Решение задач линейного программирования
графическим методом

Существуют два наиболее распространенных способа решения задач линейного программирования (ЗЛП): графический метод и симплекс-метод. Графический метод существенно нагляднее и обычно проще для понимания и решения (хотя занимает много времени, так как требует тщательного построения чертежа). Также этот метод позволяет практически одновременно найти решение на минимум и максимум, тогда как симплекс-методом придется делать «два подхода».

Основные шаги по решению ЗПЛ графическим методом следующие: построить область допустимых решений задачи (выпуклый многоугольник), который определяется как пересечение полуплоскостей, соответствующих неравенствам задачи, построить линию уровня целевой функции, и, наконец, двигать линию уровня в нужном направлении, пока не достигнем крайней точки области — оптимальной точки (или множества). При этом можно найти единственное оптимальное решение (точку), множество (отрезок) или ни одного (область пустая или не ограниченная в нужном направлении).

А за конкретикой — к примерам ниже: вы найдете там решенные графическим способом задачи линейного программирования. Примеры решений выложены бесплатно для вашего удобства — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий по методам оптимальных решений, перейдите в раздел: Решение задач ЛП на заказ (решаем для студентов очников и заочников).

Графический метод решения ЗЛП: примеры онлайн

Задача 1. Колхоз имеет возможность приобрести не более 19 трехтонных автомашин и не более 17 пятитонных. Отпускная цена трехтонного грузовика — 4000 руб., пятитонного — 5000 руб. Колхоз может выделить для приобретения автомашин 141 тысяч рублей. Сколько нужно приобрести автомашин, чтобы их суммарная грузоподъемность была максимальной?
Задачу решить графическими и аналитическими методами.

Задача 2. Решить задачу графическим методом на минимум и на максимум

Задача 3. Решить задачу графическим методом на минимум и на максимум

Задача 4. Среди чисел x и y, удовлетворяющих условиям

найти такие, при которых разность этих чисел y-x принимает наибольшее значение.

Задача 5. Решить графическим методом ЗЛП, заданную указанной математической моделью.

Задача 6. Решите графически следующие задачи линейного программирования

Задача 7. Решить графическим методом

Источник