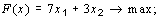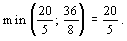Пример оптимизационной модели задача линейного программирования

19. Пример решения оптимизационной задачи линейного программирования симплексным методом

1. Построим ОМ ограничение по ресурсу А;ограничение по ресурсу В. 2. Преобразуем задачу в приведенную каноническую форму. Для этого достаточно ввести дополнительные переменные x3 и x4 . В результате неравенства преобразуются в строгие равенства:Построим исходную симплексную таблицу и найдем начальное базисное решение. Им будет пара значений дополнительных переменных, которым соответствует единичная подматрица х3=20 и х4=36.

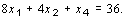
1-я итерация . Находим генеральный столбец и генеральную строку:

Генеральный элемент равняется 5.

2-я итерация . Найденное базисное решение не является оптимальным, так как строка оценок ( F j — C j ) содержит один положительный элемент. Находим генеральный столбец и генеральную строку: max(0,0,3,-1,4,0)=0,2

Найденное решение оптимально, так как все специальные оценки целевой функции (Fj — Cj) равны нулю или отрицательны. F (x) =29; x1=2; x2 =5.

20. Двойственная задача линейного програмирования

Двойственная задача ЛП может быть сформулирована следующим образом: найти переменные yi(i =1,2, . m), при которых целевая функция была бы минимальной

не нарушая ограничений

Данная задача называется двойственной. Компоненты решения двойственной задачи называются объективно обусловленными оценками .

Прямая и обратная задачи ЛП связаны между собой теоремами двойственности. Первая теорема двойственности . Если обе задачи имеют допустимые решения, то они имеют и оптимальное решение, причем значение целевых функций у них будет одинаково

илиЕсли же хотя бы одна из задач не имеет допустимого решения, то ни одна из них не имеет оптимального решения. Вторая теорема двойственности (теорема о дополняющей нежесткости). Для того чтобы векторыибыли оптимальными решениями соответственно прямой и двойственной задачи, необходимо и достаточно, чтобы выполнялись следующие условия:

Следствие 1 . Пусть оптимальное значение некоторой переменной двойственной задачи строго положительно

Тогда из условия (1) получим

или Экономический смысл данных выражений можно интерпретировать в следующей редакции. Если объективно обусловленная оценка некоторого ресурса больше нуля (строго положительна), то этот ресурс полностью (без остатка) расходуется в процессе выполнения оптимального плана. Следствие 2 . Пусть для оптимального значения некоторой переменной x i прямой задачи выполняется условие строгого неравенстваТогда, основываясь на том же первом условии (1), можно заключить, что y i = 0.

Экономически это означает, что если в оптимальном плане какой-то ресурс используется не полностью, то его объективно обусловленная оценка обязательно равна нулю.

Источник

2.2. Общая экономико-математическая модель линейного программирования

Как правило, в общем виде оптимизационная модель формируется следующим образом: надо отыскать значения управляемых параметров (показателей) x₁, x₂, . x_n, характеризующих управляемый экономический объект или процесс, придающие максимальное или минимальное значение целевой функции F (x₁, x₂, . x_n)при соблюдении ограничений, накладываемых на область изменения показателейx₁, x₂, . x_n, и связей между ними в виде системы из m неравенств и/или уравнений. Если целевая функция и все ограничения между искомыми показателями выражены в виде линейных зависимостей, то оптимизационная модель сводится к задаче линейного математического программирования и саму модель также называют линейной.

В математической форме задачу линейного программирования можно записать в следующем виде: среди решений системы изm линейных уравнений (неравенств) с n неизвестными

(2.1)

найти такой, при котором целевая функция линейной формы

(2.2)

достигает экстремального (максимального или минимального) значения.

Коефициенты – заданные константы (известные числовые значения).

В общей задачи линейного программирования используются следующие понятия.

Вектор , координаты (значения) которого удовлетворяют ограничения системы (2.1), называется планом или допустимым решением.

Совокупность всех допустимых решений (планов) задачи линейного программирования образует область допустимых решений.

Оптимальным планом или оптимальным решением задачи линейного программирования называется допустимый план, при котором целевая функция достигает своего экстремального значения.

2.3. Примеры линейных оптимизационных задач

Приведем несколько формализованных типичных постановок экономических задач, решаемых методами линейного программирования.

1. Задача оптимизации производства (планирования производства или об использовании ресурсов)

Некоторое предприятие выпускает n видов продукции. Руководству необходимо решить, какое именно количество каждого продукта необходимо производить, т.е. нужно составить план производства – вектор , где– количество единицj-го вида продукции . При этом считается, что предприятие располагает ограниченными ресурсами, объем которых известен (значения b_i ). Технологические возможности производства определяются значениями коэффициентов , показывающих какое количествоi-го ресурса необходимо потратить для выпуска одной единицы j-го продукта. В случае линейной задачи математического программирования технология производства считается линейной, т.е. предполагается, что все затраты ресурсов растут прямо пропорционально объемам выпуска.

Устанавливаемый руководителем план должен обладать экстремальными свойствами, т.е. должен обеспечить максимальную прибыль предприятию, если известно, что от продажи одной единицы j-го продукта предприятие получает прибыль в размере с_j .

Математическая модель данной задачи такова:

найти максимум функции при условиях:

2. Задача составления рациона («на диету»)

Некоторый рацион состоит из нескольких видов продуктов питания . Известны: стоимость единицы каждого компонента рациона с_j, минимальная потребность организма в питательных веществах (жиры, белки, углеводы, витамины и др.), содержание каждого питательного вещества в единице каждого продукта . Необходимо составить рацион, обеспечивающий организм количеством питательных веществ не менее минимальной потребности и с наименьшими затратами денежных средств продукты питания.

Математическая модель задачи: найти минимум функции при условиях:

3. Задача оптимального распределения производственных мощностей предприятий.

Есть несколько предприятий, производящих определенное количество видов продукции. Известны: фонд рабочего времени каждого предприятия; потребности в продукции каждого вида; матрица мощностей производства всех видов продукции, изготавливаемых на каждом предприятии; себестоимости производства единицы продукции каждого предприятия. Необходимо распределить производство продукции между предприятиями таким образом, чтобы удовлетворить потребности в изготовлении продукции и максимально использовать производственные мощности предприятий.

Критерий оптимальности – минимальные суммарные затраты на изготовление продукции либо максимальное использование производственных мощностей.

4. Транспортная задача

В данной задаче рассматривается определенное количество пунктов производства и потребления некоторой однородной продукции (количество пунктов производства и потребления может совпадать и не совпадать). Известны объемы произведенной продукции в каждом пункте производства и потребности каждого пункта потребления. Задана стоимость транспортировки единицы продукции от каждого пункта производства к каждому пункту потребления. Необходимо определить оптимальные объемы перевозок продукции, т.е. такие, которые бы минимизировали суммарную стоимость транспортировки продукции и при которых были бы учтены условия вывоза продукции от производителей и обеспечения требований потребителей в продукции нужного им количества.

Источник