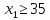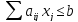Применение задач математического программирования

1. Определение задачи математического программирования

Математическое программирование — это область математики, разрабатывающая теорию, решения многомерных задач с ограничениями. В отличие от классической математики, мы находим наилучший вариант из всех возможных.

Итак, математическое программирование — это раздел высшей математики, занимающийся решением задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.

Общая задача М. п. состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

Классическая задача математического программирования – задача выбора таких значений некоторых переменных, подчиненных системе ограничений в форме равенств, при которых достигается max или min функции.

2. Допустимое решение задачи, одр, оптимальное решение задачи.

Допустимым решением задачи называется любой n-мерный вектор

x (x = (,,…,)), удовлетворяющий системе ограничений и условию неотрицательности.

Множество допустимых решений образует ОДР.

Оптимальным решением задачи называется такое допустимое решение, при котором целевая функция достигает экстремума.

3. Экономико–математические модели задач лп: задача о банке

К экономико-математическим моделям задач ЛП относятся:Задача планирования производства, определения оптимального ассортимента продукции, о диете, о банке, составления жидких смесей, Транспортная задача

Построение экономико – математической модели.

Задача о банке

Собственные средства банка в сумме с депозитами составляют 100 млн. $. Не менее 35 млн. $ из этой суммы размещена в кредитах (не ликвид). Ликвидное ограничение ценных бумаг должны составлять не менее 30 %, размещенных в кредитах и ликвидных активах.

Пусть 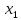— средства, размещенные в кредитах,– средства, размещенные в ликвидных активах.

Банк. Огран. (1)

Кред. Огран.

Ликвид. Огран.

Условие неопределенности ,≥0 (4)

— доходность кредитов, — доходность ликвидных активов

F = при услов. (1) – (4).

4. Экономико – математические модели задач лп: задача определения оптимального ассортимента продукции.

— П1, — П2

F = 3

2

3

5. Задача лп, стандартная форма, каноническая форма.

К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

В общем виде модель записывается следующим образом:

Целевая функция: F (x)= c1x1 + c2x2 + . + cnxn → max(min)

ограничения: a11x1 + a12x2 + . + a1nxn b1,

требование неотрицательности: xj ≥ 0,

Задача имеет каноническую форму, если является задачей на максимум (минимум) линейной функции F и ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х1, х2, . хn являются неотрицательными:

F (x) =

, i= 1,2…m

, j = 1,2…n

В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной функции f и система ограничений ее состоит из одних линейных неравенств типа «

F (x) =

, i= 1,2…m

, j = 1,2…n

Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.

Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации — ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.

Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума)

Источник

Раздел II. Задачи математического программирования

В этом разделе показано применение различных методов решения задач математического программирования (задач линейного программирования, транспортных задач). Для каждого метода приводится подробное решение примеров, аналогичных 2-му, 3-му и 4-му заданиям контрольной работы.

§1 Основные сведения из теории линейного программирования.

Задача математического программирования (3)(или (4))называется задачей линейного программирования (ЛП), если целевая функцияfесть линейная функция, а множество допустимых решений Х задается с помощью линейных неравенств или линейных уравнений:

(1)-(3) -это стандартная постановка задачи ЛП (в общем случае в ограничениях (2) могут быть различные соотношения вида “≥”, “≤”, “=”).Здесьc₁,…,c_n — коэффициенты при целевой функции,a₁₁. a_nn -коэффициенты при ограничениях,b₁,…,b_k— свободные члены при ограничениях. Все они являются известными числами (заданы); Неизвестными являются переменныеx₁,…,x_n

В задачах (1) — (3)требуется найти такие значения переменныхx₁*. x_n* (точку максимума), чтобы:

1)Эти переменные удовлетворяли воем ограничениям (2)и (3)(условие допустимости);

2)В точке х* = (х₁*. x_n* )целевая функцияfпринимала максимальное значениеf(x*) (условие оптимальности).

Аналогично ставится задача на минимум.

Свойства задач линейного программирования

1.Допустимое множество задачи ЛП либо пусто, либо является выпуклым многогранником вR n (как пересечение полупространств, описываемых неравенствами (2)-(3)). Оно может быть кfк ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.

2.Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации — ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.

3.Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечное множество точек максимума или минимума).

Методами решения задач ЛП являются: графический метод (в случае двух переменных), симплекс-метод или его разновидности (в общем случае).

§2. Решение задачи лп графическим методом :

Пример 1,(случаи единственного оптимального решения). Используя графический метод, найти решение следующей задачи ЛП:

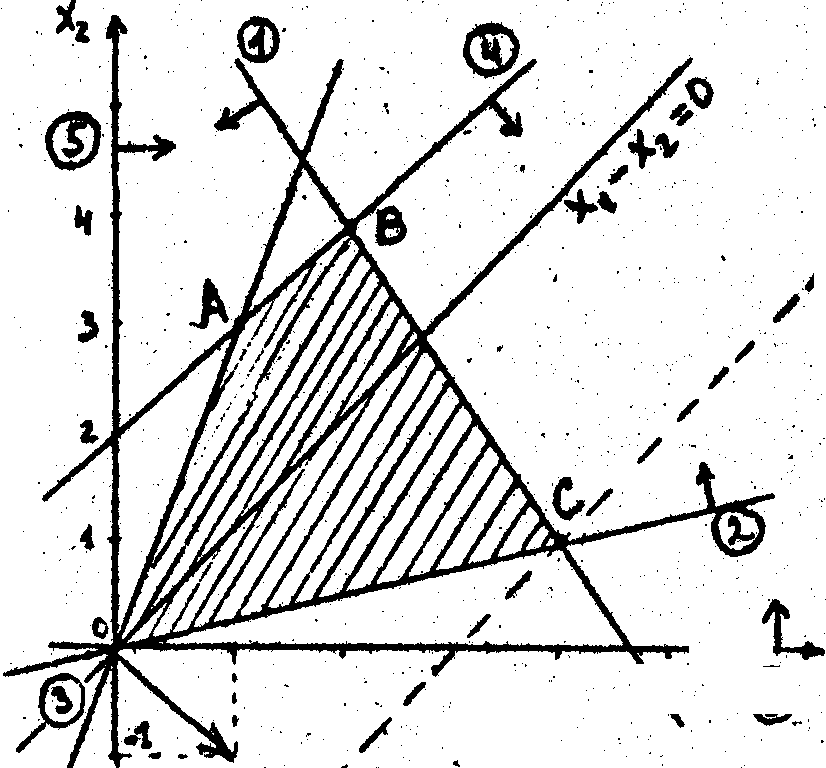
Решение. На плоскости R 2 построим допустимое множество, описываемое шестью неравенствами. Это будет пересечение шести полуплоскостей (каждое неравенство-ограничение задает на R 2 полуплоскость). Например, первую полуплоскость 3x₁+2х₂≤14 строим так. Проводим прямую 3x₁+2х₂=14, которая является границей этой полуплоскости. Чтобы определить, какую из полуплоскостей, лежащих по обе стороны от прямой 3x₁+2х₂=14, описывает неравенство 3x₁+2х₂≤14, достаточно поставить в это неравенство координаты начала координат, т.е. (0,0). Если неравенство выполняется, то берем ту полуплоскость, которая содержит начало координат, если не выполняется, то берем полуплоскость, не содержащую начала координат. В нашем случае 3*0 + 2*0≤14. На рис. 1в кружочках написаны номера линий (границ полуплоскостей), а полуплоскости обозначены стрелками. В результате пересечения построенных шести полуплоскостей получаем многогранник ОАВС. который и является допус­тимым множеством нашей задачи. Можно проверить, что любая точка этого многогранника удовлетворяет всем шести неравенствам, а для любой точки вне этого многогранника хотя бы одно неравенство из шести будет нарушено.

Таким образом, геометрически наша задача свелась к тому, чтобы в пределах многогранника ОАВС найти точку х* =(x₁*,x₂*). в которой целевая функцийf(x) =x₁-x₂получит максимальное значение.

Благодаря свойству 3(см. выше) мы заранее знаем, что точкой максимума нашей целевой функции является одна или некоторые из вершин О,А,В или С.

Для того, чтобы определить эту вершину, проведем какую-либо линию уровня целевой функции, т.е. проведем прямую f(x)=с₁, где с-const. Для простоты возьмем с=0,тогда линия уровня есть x₁-x₂=0.Увеличивая правую часть этого уравнения (например,x₁-x₂=1, x₁-x₂=3и т.д.), мы обнаружим параллельное смещение линии уровня вниз, причем, чем больше правая часть, тем дальше. Если же уменьшим правую часть (например, x₁-x₂=-1,x₁-x₂=-2и т.д.), то наблюдаем смещение вверх.

Отсюда понятно, что, смещая линию уровня в сторону возрастания целевой функции, мы найдем ту вершину многогранника ОАВС, которая соответствует точке максимума. Как видно из рисунка 1,это есть точка С.

Чтобы сразу определить направление возрастания функции t, вычисляют ее градиентf. Для линейной функции градиент всегда равен вектору, составленному из коэффициентов этой функции.

Для нашей целевой функции f(x)= x₁-x₂градиент f =(1,-1) (см. рис, 1). Известно, что градиент перпендикулярен линии уровня и показывает направление возрастания функции, а антиградиент, т.е. вектор -fпоказывает направление убывания функции.

Итак, «двигая» линию уровня x₁-x₂=0в сторону вектора f,находим точку максимума С.

Координаты точки С найдем решая совместно уравнения линий 1и 2, пересекающихся в точке С:

Ответ: х*=(4,1) -точка максимума,

f(x*) = 3 -максимальное значение целевой функции.

Отсюда получаем алгоритм графического метода:

1)построить на плоскости допустимое множество,

2)построитьлинию уровня целевой функции,

3)построитьградиент (в задаче на максимум) или антиградиент (в задаче на минимум) целевой функции,

4)найтии вычислить координаты точки максимума или минимум,

5)вычислить значение целевой функции в найденной точке.

Пример 2.(Случай бесконечного множества оптимальных решений):

Как видно из рис. 2,наиболее удаленным в сторону антиградиента -f=(1,2)местом касания линии уровняf(x)=с с допустимым множествомOABCDявляется грань ВС (т.е. выпуклая оболочка вершинB=(l, 3)и С=(3,2)).Поэтому любая точка грани ВС является точкой минимума целевой функции.

Ответ: х*=(1,3)+(1-)(3,2)=(3-2,2+) для любого[0, 1] — точка минимума,

f(x*)=-7 — минимальное значение целевой функции.

Пример 3.(Случай отсутствия оптимального решения ввиду неограниченности целевой функции на допустимом множестве):

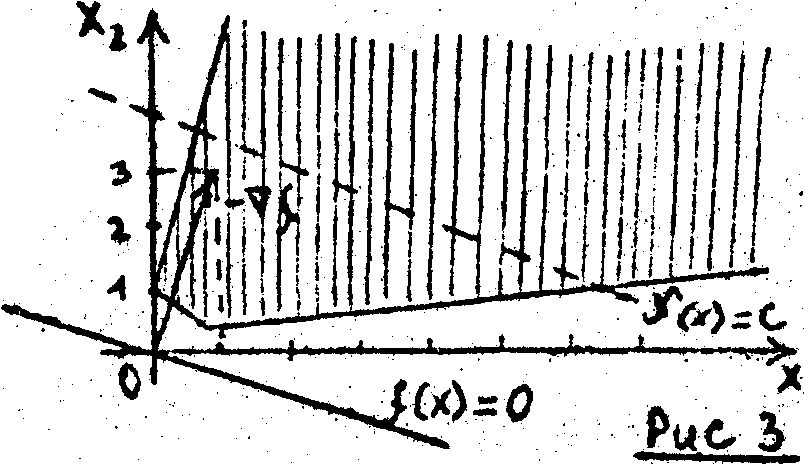
Допустимое множество этой задачи представляет собой неограниченный многогранник (рис. 3).

При параллельном переносе линии уровня f(x)=с вдоль антиградиента -f=(1,2) она всегда пересекает допустимое множество, т.е. нет «наиболее удаленной точки касания», а целевая функция неограниченно убывает.

Ответ:Точки минимума нет; целевая функция неограниченна снизу.

Пример 4.(Случай отсутствия оптимального решения ввиду пустоты допустимого множества):

Как показано на рис, 4,полуплоскости, образованные первыми двумя неравенствами, не пересекаются (система не совместна); Поэтому нет ни одной допустимой точки.

Графический метод применяется и в том случае, когда в задаче ЛП число линейно независимых ограничений-неравенств (каноническая форма) ровно на два меньше числа переменных. Об этом подробно можно почитать, например, в [8, стр. 49].

Источник