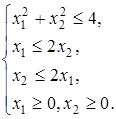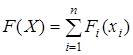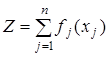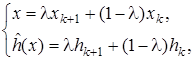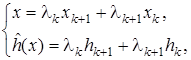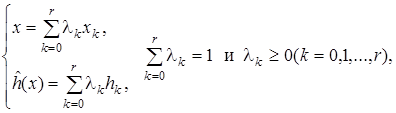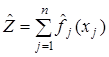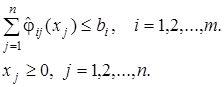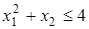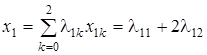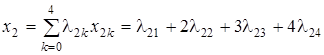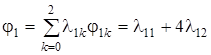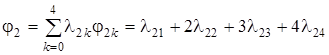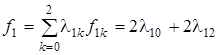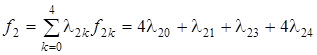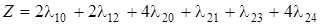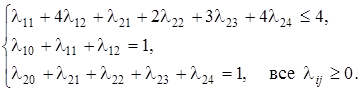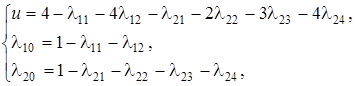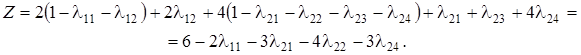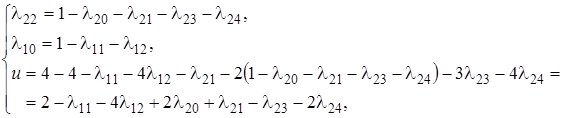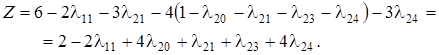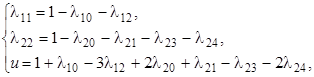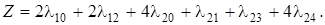Приближенное решение задач выпуклого программирования

Приближенное решение задач выпуклого программирования методом кусочно-линейной аппроксимации

причем все функции j _i (Х) является выпуклыми на некотором выпуклом множестве М, а функция Z либо выпукла на множестве М, либо вогнута. Задача выпуклого программирования (ВП) состоит в отыскании такого решения системы ограничений (11.6), при котором целевая функция Z достигает минимального значения, или вогнутая функция Z достигает максимального значения. (Условия неотрицательности переменных можно считать включенными в систему (11.6)).

Ввиду свойства 3 (разд. 11.1) всякая задача линейного программирования является частным случаем задачи ВП. В общем случае задачи ВП являются задачами нелинейного программирования. Выделение задач ВП в специальный класс объясняется экстремальными свойствами выпуклых функций: всякий локальный минимум выпуклой функции (локальный максимум вогнутой функции) является одновременно и глобальным; кроме того, ввиду свойства 2 выпуклая (вогнутая) функция, заданная на замкнутом ограниченном множестве, достигает на этом множестве глобального максимума и глобального минимума. Отсюда вытекает, что если целевая функция Z является строго выпуклой (строго вогнутой) и если область решений системы ограничений не пуста и ограничена, то задача ВП всегда имеет единственное решение. В этом случае минимум выпуклой (максимум вогнутой) функции достигается внутри области решений, если там имеется стационарная точка, или на границе этой области, если внутри нее нет стационарной точки. (В общем случае можно утверждать лишь, что множество оптимальных решений любой задачи ВП является выпуклым множеством).

Ñ 11. 4. Геометрически решить следующую задачу ВП: найти минимум функции Z = 2 + (x ₁ — 1) 2 + (x ₂ -1) 2 при ограничениях:

Решение. Строим область допустимых решений данной задачи:

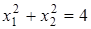
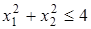
а) — окружность с центром в начале координат и радиусом R =2. (рис. 11.3). Область решений неравенства состоит из точек, лежащих внутри этой окружности и на ней самой;

б) x ₁ = 2 x ₂ — прямая, которую можно построить, например, по точкам (0; 0) и (2; 1). Область решений неравенства x ₁ £ 2 x ₂ — полуплоскость, лежащая над этой прямой, включая и саму прямую;

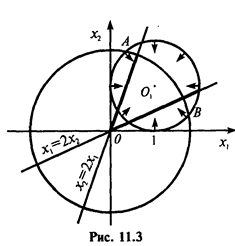в) x ₂ = 2 x ₁ — прямая, которая строится, например, по точкам (0; 0) и (1; 2). Область решений неравенства x ₂ £ 2 x ₁ — полуплоскость, лежащая под этой прямой, включая и саму прямую. Таким образом, с учетом условий неотрицательности переменных, областью допустимых решений данной задачи является замкнутый сектор ОАВ (рис. 11.3).

Теперь построим линию уровня функции Z и определим направление убывания Z. Все линии уровня имеют уравнение Z = С, т.е. (x ₁ ‑ 1) 2 + (x ₂ ‑ 1) 2 = С — 2. При C = 3 получаем линию уровня (x ₁ ‑ 1) 2 + (x ₂ ‑ 1) 2 = 1 — это окружность с центром в точке 0 ₁(1; 1) и радиусом R = 1. Ясно, что в любой точке этой линии уровня при перемещении от центра окружности 0 ₁ функция Z возрастает, а при перемещении к центру — убывает. Таким образом, минимум Z достигается в точке (1; 1), Z _min = 2 (нетрудно убедиться, что точка (1; 1) является стационарной точкой функции Z). Ñ

Функция F (X) = F (x ₁, x ₂, …, x_n) называется сепарабельной, если ее можно представить в виде суммы функций, каждая из которых зависит только от одной переменной, т.е. если

F (X) =F ₁(x ₁) + F (x ₂) + … + F_n (x_n), или (11. 8)

(не исключено, что F_i (х_i) = 0 при некоторых i).

Пусть в задаче ВП (11.6), (11.7) и функция цели Z, и все ограничения j _i являются сепарабельными. Тогда задача имеет вид: найти минимум выпуклой (максимум — вогнутой) функции при ограничениях

. (11. 9)

Идея метода кусочно-линейной аппроксимации состоит в том, что все f_i и все j _ij заменяются ломаными линиями, состоящими из прямолинейных отрезков. При этом исходная задача ВП заменяется новой, приближенной задачей, которая является задачей линейного программирования. Эта задача решается обычно симплексным методом, и ее решение является приближенным решением исходной задачи ВП.

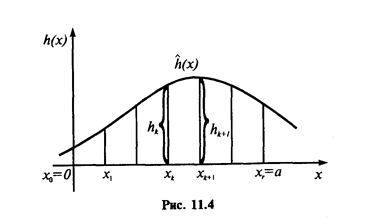
Для построения приближенной задачи рассмотрим кусочно-линейную аппроксимацию функции одной переменной h (x), за данной на отрезке [0, a ]. Разобьем этот отрезок на r частей точками x ₀ < x₁ < … < x_r так, чтобы x ₀ = 0, x_r = a (рис. 11.4). Вычислим значения функции h_k (x)(k = 0, …, r) в этих точках. Соединим попарно точки (x_k; h_k) и (x_{k +1}; h_{k +1}) отрезками прямых. Состоящая из этих отрезков ломаная аппроксимирует функцию h (x) на отрезке [0, a ]. (Не рассматривая здесь оценку точности приближения, отметим только, что точность можно увеличить за счет более мелкого разбиения отрезка).

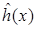
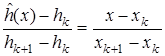
Уравнение участка ломаной между точками (x_k; h_k) и (x_{k +1}; h_{k +1}) имеет вид (уравнение прямой по двум точкам). Если каждое из отношений в этом равенстве обозначить через l, то получим:

. (11. 10)

Отметим, что для каждого x Î [ x_k; x_{k +1}] существует единственное значение l, удовлетворяющее условиям (11.10) (см. уравнение отрезка (11.2)). Обозначив 1 — l = l _k, l = l _k, можно переписать (11.10) в виде:

. (11. 11)

(Уравнения (11.11) называются параметрическими уравнениями отрезка. Если h (x)= 0, то второе из этих уравнений обращается в тождество 0 = 0, а первое принимает вид (11.2) — уравнение отрезка, лежащего на оси абсцисс.)

Таким образом, для любого x Î [0, a ] уравнение ломаной можно записать в виде:

. (11. 12)

причем всегда отличны от нуля только два значения l _k (если x является внутренней точкой k -го отрезка разбиения) или одно (если x совпадает с концом отрезка).

Возвращаясь к задаче ВП с сепарабельными функциями, отметим, что прежде всего (в зависимости от системы ограничений) нужно определить интервал изменения каждой переменной x_j. Затем каждый этот интервал разбивается на части точками x_jk и с использованием формул (11.12) строится кусочно-линейная аппроксимация для функций f_j и j _ij. После этого можно для исходной задачи(11. 9) записать приближенную задачу:

найти максимум функции

при ограничениях (11.13)

Поскольку приближенная задача (11.13) является задачей линейного программирования и мы обычно решаем ее симплексным методом, условия неотрицательности переменных записываются отдельно от остальных ограничений. Отличие полученной задачи (11.13) от обычной задачи линейного программирования состоит в том, что для каждого x_j имеется не более двух соседних ненулевых l _jk и, значит, нельзя брать в качестве основных переменных два l _jk с одинаковым j и несоседними k. Заметим также, что для условий неотрицательности переменных слагаемых f_j (x_j) и j_ij(x_j) (если таковые окажутся) кусочно-линейную аппроксимацию проводить, конечно, не нужно.

Ñ 11. 5. Найти минимум функции Z = 2(x ₁ — 1) 2 + (x ₂ — 2) 2 при ограничениях:

Решить данную задачу методом кусочно-линейной аппроксимации.

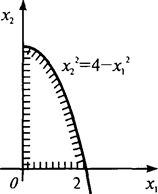
Решение. Прежде всего рекомендуем самостоятельно убедиться в том, что данная задача является задачей ВП (используйте критерий Сильвестра, см. задачу (11.2) Далее, при условии неотрицательности переменных неравенство показывает, что x ₁ может изменяться лишь от 0 до 2, а x ₂ — от 0 до 4 (см. рис. 11.5).

Отрезок [0; 2] разобьем точками x ₁₀ = 0, x ₁₁ = 1, x ₁₂ = 2, а отрезок [0; 4] — точками x ₂₀ = 0, x ₂₁ = 1, x ₂₂ = 2, x ₂₃ = 3, x ₂₄ = 4. Сравнивая условие данной задачи с (11.9), видим, что

Удобно сначала вычислить необходимые значения этих функций (так как имеем лишь одно ограничение, т.е. m = 1, будем писать j₁ и j₂ вместо j₁₁ и j₁₂).

,

,

,

,

,

.

Таким образом, приближенная задача (11.13) для данной задачи ВП имеет вид: найти минимум функции

Это задача линейного программирования с 8 переменными l _ij. Для решения ее симплексным методом первое ограничение-неравенство нужно преобразовать в уравнение путем введения дополнительной неотрицательной переменной, которую обо значим u:

Тогда система ограничений станет системой трех уравнений с 9 переменными, т.е. 3 переменные нужно взять за основные (берем и, l₁₀ и l₂₀, так как они входят только в одно уравнение каждая), а остальные 6 являются свободными. Как обычно, на каждом шаге решения основные переменные и функция цели выражаются через свободные.

Так как в выражении Z имеются свободные переменные с отрицательными коэффициентами, то I базисное решение неоптимальное (хотя и допустимое), и согласно алгоритму симплексного метода l₂₂ следует перевести в основные переменные. Находим min = 1, выделяем третье уравнение и переменную l₂₀ переводим в свободные переменные.

II шаг. Основные переменные l₂₂, l₁₀, u.

III шаг. Основные переменные l₁₁, l₂₂, u.

Критерий оптимальности симплексного метода выполнен, значит на III шаге получено оптимальное базисное решение:

Переходя к исходным переменным x ₁, x ₂, получаем:

Таким образом, оптимальное решение приближенной задачи (1; 2) и Z _min = 0.Ñ

Можно было бы геометрически решить исходную задачу ВП и убедиться в том, что оптимальное решение приближенной задачи в точности совпадает с оптимальным решением исходной задачи. Это совпадение случайное. В общем случае полученное решение является лишь некоторым приближением оптимального решения исходной задачи. Улучшить точность приближения можно, разбивая на более мелкие части уже не исходные отрезки изменения переменных, а другие, меньшие, взятые в окрестности полученного первого приближения. Недостатком метода является большое увеличение размерности задачи (т.е. числа переменных) при пере ходе к приближенной линейной модели.

Источник