Python для анализа данных¶
Нам пригодится только модуль scipy.stats . Полное описание доступно по ссылке. По ссылке можно прочитать полную документацию по работе с непрерывными (Continuous), дискретными (Discrete) и многомерными (Multivariate) распределениями. Пакет также предоставляет некоторое количество статистических методов, которые рассматриваются в курсах статистики.
import scipy.stats as sps import numpy as np import ipywidgets as widgets import matplotlib.pyplot as plt %matplotlib inline
1. Работа с библиотекой scipy.stats .¶
- X(params).rvs(size=N) — генерация выборки размера $N$ (Random VariateS). Возвращает numpy.array ;
- X(params).cdf(x) — значение функции распределения в точке $x$ (Cumulative Distribution Function);
- X(params).logcdf(x) — значение логарифма функции распределения в точке $x$;
- X(params).ppf(q) — $q$-квантиль (Percent Point Function);
- X(params).mean() — математическое ожидание;
- X(params).median() — медиана ($1/2$-квантиль);
- X(params).var() — дисперсия (Variance);
- X(params).std() — стандартное отклонение = корень из дисперсии (Standard Deviation).
Кроме того для непрерывных распределений определены функции
- X(params).pdf(x) — значение плотности в точке $x$ (Probability Density Function);
- X(params).logpdf(x) — значение логарифма плотности в точке $x$.
- X(params).pmf(k) — значение дискретной плотности в точке $k$ (Probability Mass Function);
- X(params).logpdf(k) — значение логарифма дискретной плотности в точке $k$.
Все перечисленные выше методы применимы как к конкретному распределению X(params) , так и к самому классу X . Во втором случае параметры передаются в сам метод. Например, вызов X.rvs(size=N, params) эквивалентен X(params).rvs(size=N) . При работе с распределениями и случайными величинами рекомендуем использовать первый способ, посколько он больше согласуется с математическим синтаксисом теории вероятностей.
Параметры могут быть следующими:
- loc — параметр сдвига;
- scale — параметр масштаба;
- и другие параметры (например, $n$ и $p$ для биномиального).
Для примера сгенерируем выборку размера $N = 200$ из распределения $\mathcal(1, 9)$ и посчитаем некоторые статистики. В терминах выше описанных функций у нас $X$ = sps.norm , а params = ( loc=1, scale=3 ).
Примечание. Выборка — набор независимых одинаково распределенных случайных величин. Часто в разговорной речи выборку отождествляют с ее реализацией — значения случайных величин из выборки при «выпавшем» элементарном исходе.
sample = sps.norm(loc=1, scale=3).rvs(size=200) print('Первые 10 значений выборки:\n', sample[:10]) print('Выборочное среденее: %.3f' % sample.mean()) print('Выборочная дисперсия: %.3f' % sample.var())
Первые 10 значений выборки: [ 0.65179639 -0.66437884 0.61450407 -0.1828078 0.42271419 0.14424901 2.01547486 7.81094724 -1.35246891 -1.35574313] Выборочное среденее: 0.854 Выборочная дисперсия: 9.118
Как в python можно реализовать эмпирическую функцию распределения?
Здравствуйте, мне бы хотелось узнать как можно реализовать в python отрисовку эмперической функции вида:
с выборкой:
[-1.97, -0.736, -0.152, -0.049, -0.044, -0.029, 0.089, 0.306, 0.349, 0.413,
0.48, 0.518, 0.666, 0.691, 0.748, 0.834, 0.865, 0.866, 0.929, 0.974,
1.024, 1.096, 1.138, 1.197, 1.221, 1.258, 1.296, 0.426, 1.461, 1.537,
1.589, 1.679, 1.783, 1.833, 1.9, 1.922, 1.938, 1.954, 1.965, 1.976,
2.039, 2.047, 2.076, 2.261, 2.295, 2.453, 2.569, 2.604, 2.963, 3.031]
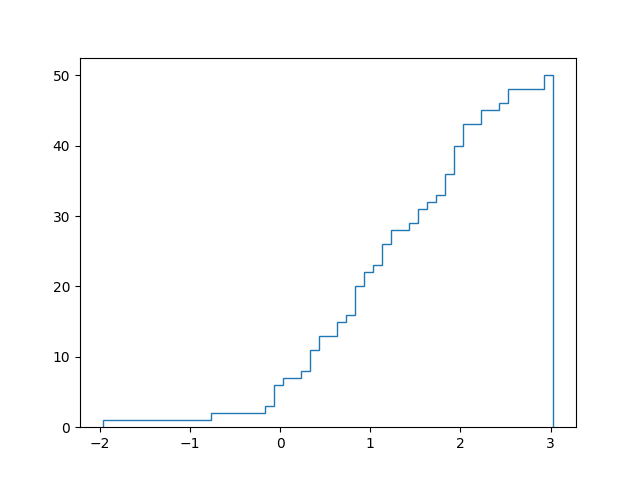
Пробовал в matplotlab и tkinter но дальше ступенчатой не ушел, заранее спасибо за помощь!
Простой 3 комментария
plt.hist(lst, histtype='step', cumulative=True, bins=len(lst))результат:
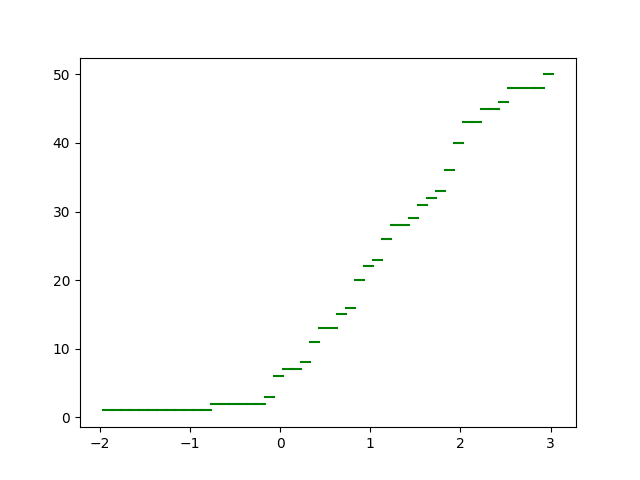
bin_dt, bin_gr = np.histogram(lst, bins=len(lst)) Y = bin_dt.cumsum() for i in range(len(Y)): plt.plot([bin_gr[i], bin_gr[i+1]],[Y[i], Y[i]],color='green')Результат:
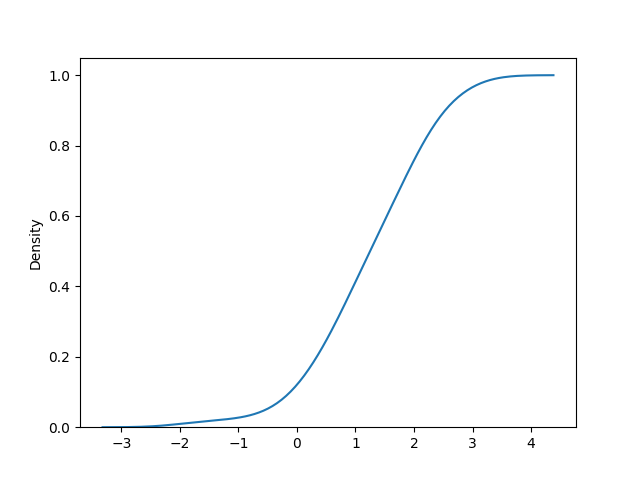
import seaborn as sns sns.kdeplot(lst, cumulative=True)Результат:
Здравствуйте, спасибо за ваш ответ. Там расстояния разные, так как точки некоторые в выборке повторяются, а такого быть по идее не должно, у меня тоже был подобный результат как вы привели во втором примере, меня интересует как можно проблему с разными расстояниями решить чтобы диапазон был от 0 до 1 как в примере который я указывал в вопросе.
DemonDED,
Какие «разные расстояния»? Между чем и чем? Более того, какие «повторяющиеся точки» в вашей выборке? Покажите их в вашем примере?
Во-вторых. Вы запросили построение эмпирической функции распределения. Она и построена. Для построения эмпирической функции по оси Х откладываются значения ваших данных (это — из определения функции распределения). Откуда там на вашем рисунке может взяться 1,2,3. 10, если ваши данные находятся в диапазоне от -1.97 до +3.3?
В-третьих. По определению эмпирическая функция распределения в случае дискретных значений строиться так: для каждой точки х вашей выборки, откладываемой по оси Х, значением Y есть вероятность того, что наугад взятый элементов вашей выборке окажется меньшим, чем значение х. (ну, или если совсем «по-простому», доля элементов выборки менших х). Для того, что бы из моих рисунков 1 и 2 действительно получить eCDF, надо значения по оси Y разделить на количество элементов в выборке. На форму самого графика это не повлияет никак, а значения по оси Y просто окажутся пронормированы от 0 до 1. Я это не сделал, но надеюсь для вас дополнить соответствующим образом скрипты сложности не представит.
Ну и в-четвертых. Я построил то что вы просили — эмпирическую функцию распределения. Построил строго по определению. Из вашего комментария к моему вопросу можно заключить, что на самом деле вы хотели построить что-то другое но почему-то решили назвать это «эмпирической функцией распределения». Но что именно — ведомо только вам одному. Поэтому, если нужна дальнейшая помощь, сформулируйте четко и однозначно, желательно в общепринятой терминологии и не используя термины не по назначению, что-же за такой дивный график у вас должен получиться и что именно на нем должно быть отображено.
dmshar, расстояния изменяются по оси ОУ, как верно было подмечено, на которой у нас отмечена вероятность «достать конкретный элемент выборки».
под расстояниями подразумевается разность, между вероятностью предписанной на графике элементу Х(к) и Х(к-1) (в скобочках индексы).
так как выборка — это набор одинаково распределенных и независимых величин, то вероятность вытащить любой элемент будет равна вероятности вытащить любой другой элемент.
в предоставленной выборке значения не повторяются — то есть, попасть в любое значение точно так же имеет вероятность равную попасть в любое другое значение => эти расстояния должны быть равны
при этом, каждая вероятность отмеченная на графике эфр = Р(Хi то есть если слева от t у нас 7 элементов выборки (коих всего 50, допустим), то значение на оси ОУ в этой точке будет равно 7/50
соответственно, рассматривая это в каждой точке, мы получим, что все «расстояния» должн быть равны 1/50 по ОУ