Построить фазовый портрет python

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Python package to plot phase portraits of 2D differential equations.

License

jmoy/plotdf

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Plot phase portraits of 2D differential equations using Python’s matplotlib and scipy libraries.

Inspired by Maxima’s plotdf function.

To plot dx/dt = y , dy/dt = -g sin(x) / l — b y/ (m l) :

 from math import sin from plotdf import plotdf def f(x,g=1,l=1,m=1,b=1): return np.array([x[1],-g*sin(x[0])/l-b*x[1]/m/l]) plotdf(f, # Function giving the rhs of the diff. eq. system np.array([-10,2]), # [xmin,xmax] np.array([-14,14]),# [ymin,ymax] [(1.05,-9),(0,5)], # list of initial values for trajectories (optional) # Additional parameters for `f` (optional) parameters=) 

For the full list of parameters to plotdf , see help(plotdf.plotdf) .

Both Python 2 and 3 are supported. You need matplotlib , numpy and scipy installed.

The package is on PyPI so you can install it with

About

Python package to plot phase portraits of 2D differential equations.

Источник

Digiratory

Лаборатория автоматизации и цифровой обработки сигналов

Построение фазовых портретов на языке Python

Фазовая траектория — след от движения изображающей точки. Фазовый портрет — это полная совокупность различных фазовых траекторий. Он хорошо иллюстрирует поведение системы и основные ее свойства, такие как точки равновесия.

С помощью фазовых портретов можно синтезировать регуляторы (Метод фазовой плоскости) или проводить анализ положений устойчивости и характера движений системы.

Рассмотрим построение фазовых портретов нелинейных динамических систем, представленных в форме обыкновенных дифференциальных уравнений

В качестве примера воспользуемся моделью маятника с вязким трением:

Где \(\omega \) — скорость, \(\theta \) — угол отклонения, \(b \) — коэффициент вязкого трения, \(с \) — коэффициент, учитывающий массу, длину и силу тяжести.

Для работы будем использовать библиотеки numpy, scipy и matplotlib для языка Python.

Блок импорта выглядит следующим образом:

import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt

Шаг 1. Реализация ОДУ в Python

Определим функцию, отвечающую за расчет ОДУ. Например, следующего вида:

def ode(y, t, b, c): theta, omega = y dydt = [omega, -b*omega - c*np.sin(theta)] return dydt

Аргументами функции являются:

• y — вектор переменных состояния
• t — время
• b, c — параметры ДУ (может быть любое количество)

Функция возвращает вектор производных.

Шаг 2. Численное решение ОДУ

Далее необходимо реализовать функцию для получения решения ОДУ с заданными начальными условиями:

def calcODE(args, y0, dy0, ts = 10, nt = 101): y0 = [y0, dy0] t = np.linspace(0, ts, nt) sol = odeint(ode, y0, t, args) return sol

Аргументами функции являются:

• args — Параметры ОДУ (см. шаг 1)
• y0— Начальные условия для первой переменной состояния
• dy0 — Начальные условия для второй переменной состояния (или в нашем случае ее производной)
• ts — длительность решения
• nt — Количество шагов в решении (= время интегрирования * шаг времени)

В 3-й строке формируется вектор временных отсчетов. В 4-й строке вызывается функция решения ОДУ.

Шаг 3. Генерация и вывод фазового портрета

Для построения фазового портрета необходимо произвести решения ОДУ с различными начальными условиями (вокруг интересующей точки). Для реализации также напишем функцию.

def drawPhasePortrait(args, deltaX = 1, deltaDX = 1, startX = 0, stopX = 5, startDX = 0, stopDX = 5, ts = 10, nt = 101): for y0 in range(startX, stopX, deltaX): for dy0 in range(startDX, stopDX, deltaDX): sol = calcODE(args, y0, dy0, ts, nt) plt.plot(sol[:, 1], sol[:, 0], 'b') plt.xlabel('x') plt.ylabel('dx/dt') plt.grid() plt.show()

Аргументами функции являются:

• args — Параметры ОДУ (см. шаг 1)
• deltaX — Шаг начальных условий по горизонтальной оси (переменной состояния)
• deltaDX — Шаг начальных условий по вертикальной оси (производной переменной состояния)
• startX — Начальное значение интервала начальных условий
• stopX — Конечное значение интервала начальных условий
• startDX — Начальное значение интервала начальных условий
• stopDX — Конечное значение интервала начальных условий
• ts — длительность решения
• nt — Количество шагов в решении (= время интегрирования * шаг времени)

Во вложенных циклах (строки 3-4) происходит перебор начальных условий дифференциального уравнения. В теле этих циклов (строки 5-6) происходит вызов функции решения ОДУ с заданными НУ и вывод фазовая траектории полученного решения.

Далее производятся нехитрые действия:

• Строка 7 — задается название оси X
• Строка 9 — задается название оси Y
• Строка 10 — выводится сетка на графике
• Строка 11 — вывод графика (рендер)

Шаг 4. Запуск построения

Запустить построение можно следующим образом:

b = 0.25 c = 5.0 args=(b, c) drawPhasePortrait(args) drawPhasePortrait(args, 1, 1, -10, 10, -5, 5, ts = 30, nt = 301)

Строка 1-2 — задание значений параметрам ОДУ

Строка 3 — формирование вектора параметров

Строка 4 — вызов функции генерации фазового портрета с параметрами «по умолчанию»

Строка 5 — вызов функции генерации фазового портрета с настроенными параметрами

Итог

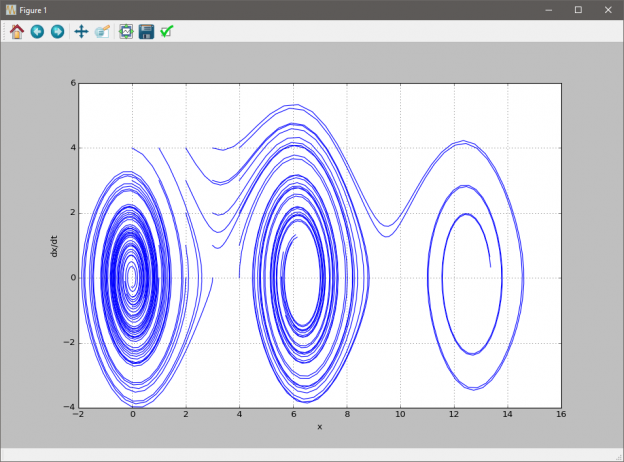
При запуске программы получаем следующий результат:

Полный текст программы под лицензией MIT (Использование при условии ссылки на источник):

# -*- coding: utf-8 -*- """ This function create a phase portrait of ode Created on Mon Jan 23 18:51:01 2017 Copyright 2017 Sinitsa AM site: digiratory.ru Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software. THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE. @author: Sinitsa AM digiratory.ru """ import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt ''' In this function you should implement your ode for example: d*theta/dt = omega d*omega/dt = -b*omega - c*np.sin(theta) @args: y - state variable t - time b, c - args of ode ''' def ode(y, t, b, c): theta, omega = y dydt = [omega, -b*omega - c*np.sin(theta)] return dydt ''' Calculate ode @args: args - arguments of ODE y0 - The initial state of y yd0 - The initial state of derivative y ts - the duration of the simulation nt - Number steps if simulation (=ts*deltat) ''' def calcODE(args, y0, dy0, ts = 10, nt = 101): y0 = [y0, dy0] t = np.linspace(0, ts, nt) sol = odeint(ode, y0, t, args) return sol ''' Drawing Phase portrait of ODE in function ode() @args: args - arguments of ODE deltaX - step x deltaDX - step derivative x startX - start value of x stopX - stop value of x startDX - start value of derivative x stopDX - stop value of derivative x ts - the duration of the simulation nt - Number steps if simulation (=ts*deltat) ''' def drawPhasePortrait(args, deltaX = 1, deltaDX = 1, startX = 0, stopX = 5, startDX = 0, stopDX = 5, ts = 10, nt = 101): for y0 in range(startX, stopX, deltaX): for dy0 in range(startDX, stopDX, deltaDX): sol = calcODE(args, y0, dy0, ts, nt) plt.plot(sol[:, 0], sol[:, 1], 'b') plt.xlabel('x') plt.ylabel('dx/dt') plt.grid() plt.show() b = 0.25 c = 5.0 args=(b, c) drawPhasePortrait(args) drawPhasePortrait(args, 1, 1, -10, 10, -5, 5, ts = 30, nt = 301)

Синица А.М.: Построение фазовых портретов на языке Python [Электронный ресурс] // Digiratory. 2017 г. URL: https://digiratory.ru/?p=435 (дата обращения: ДД.ММ.ГГГГ).

Построение фазовых портретов на языке Python : 2 комментария

Источник

Installation

Phaseportrait releases are available as wheel packages for macOS, Windows and Linux on PyPI. Install it using pip:

$ pip install phaseportrait 

Installing from source:

Open a terminal on desired route and type the following:

$ git clone https://github.com/phaseportrait/phaseportrait 

Manual installation

Visit phase-portrait webpage on GitHub. Click on green button saying Code, and download it in zip format. Save and unzip on desired directory.

What’s this?

The idea behind this project was to create a simple way to make phase portraits in 2D and 3D in Python, as we couldn’t find something similar on the internet, so we got down to work. (Update: found jmoy/plotdf, offers similar 2D phase plots but it is very limited).

Eventually, we did some work on bifurcations, 1D maps and chaos in 3D trayectories.

This idea came while taking a course in non linear dynamics and chaos, during the 3rd year of physics degree, brought by our desire of visualizing things and programming.

We want to state that we are self-taught into making this kind of stuff, and we’ve tried to make things as professionally as possible, any comments about improving our work are welcome!

Authors

Contributing

This proyect is open-source, everyone can download, use and contribute. To do that, several options are offered:

• Fork the project, add a new feature / improve the existing ones and pull a request via GitHub.
• Contact us on our emails:
  • vhloras@gmail.com
  • unaileria@gmail.com

  Источник