Построение матрицы смежности графа python

Русские Блоги

[Python] Используйте Networkx для создания различных сетевых диаграмм

Недавно участвовала в конкурсе красоты, команда выбрала тему, связанную с созданием сети. По результатам создания сети я выучил много предложений для рисования сетевых диаграмм. Теперь они организованы следующим образом:

1. Четыре типа картинок

1. Graph: Неориентированный граф, исключая тяжелые ребра,
2. MultiGraph: Неориентированный граф, может содержать тяжелые ребра
3. DiGraph: Направленный граф без тяжелых ребер
4. MultiDiGraph: Ориентированный граф, может содержать тяжелые ребра

два, nx.draw() Использование (задать вид сетевой схемы)

ВидетьРазличные параметры nx.draw ()
2.1 Параметры стиля на рисунке
node_size : Укажите размер узла (по умолчанию 300)
node_color : Укажите цвет узла (по умолчанию красный, вы можете просто определить цвет строкой, например, «r» — красный, «b» — зеленый и т. Д.)
node_shape : Форма узла (по умолчанию — круг, обозначаемый строкой «о»)
alpha : Прозрачность (по умолчанию 1.0, непрозрачный, 0 — полностью прозрачный)
width : Ширина стороны (по умолчанию 1.0)
edge_color : Цвет кромки (по умолчанию черный)
style : Стиль края (по умолчанию — реализация, необязательно: сплошной | пунктирный | пунктирный, пунктирный)
with_labels : Помечен ли узел (по умолчанию True)
font_size : Размер шрифта метки узла (по умолчанию 12)
font_color : Цвет шрифта метки узла (по умолчанию черный)
2.2 Размещение узлов на графике
circular_layout : Узлы равномерно распределены по кольцу
random_layout : Узлы распределены случайным образом
shell_layout : Узлы распределены по концентрическим кругам
spring_layout : Расположите узлы, используя алгоритм Фрухтермана-Рейнгольда (выглядит как многоцентровая радиальная диаграмма)
spectral_layout : Расположить узлы в соответствии с вектором признаков Лапласа графа.

3. Создание различных графиков (без веса)

3.1. Ненаправленный граф: График

# step1: Создайте пустое изображение import networkx as nx G=nx.Graph() # Создать пустой граф без ничего, имя графа G # step2: Добавить ребра в пустой граф выше G.add_edges_from([(1,2)]) # Здесь добавляется только одна сторона, имя начальной точки стороны 1, имя конечной точки 2 nx.draw(G,with_labels=True) # nx.draw () - это инструкция для рисования картинки, with_labels = True означает отображение имени узла на картинке import matplotlib.pyplot as plt # Рисунки и картинки с изображением пакетов и предложений plt.show() 

Конечно, если мы хотим использовать это программное обеспечение, мы должны импортировать многоугольники и узлы. Давайте добавим еще несколько ребер.

import networkx as nx G=nx.Graph() # Создать пустой граф без ничего, имя графа G G.add_edges_from([(1,2),(2,3),(3,4),(4,5)]) # (Начало стороны, конец стороны) nx.draw(G,with_labels=True) import matplotlib.pyplot as plt plt.show() 

Затем используйте список, чтобы добавить границы к графику.

# step1: Создайте пустое изображение import networkx as nx G=nx.Graph() # Создать пустое изображение без ничего # step2: Добавить ребра в пустой граф выше start=[1,3,5,7]# Список отправной точки Edge, пожалуйста, импортируйте оператор начальной точки самостоятельно to=[2,4,6,8]#Edge список конечных точек, пожалуйста, импортируйте оператор конечной точки самостоятельно, элементы в одной и той же позиции в начале и в списках соответствуют один за другим for j in range(len(start)): G.add_edge(start[j], to[j]) # G.add_edge () - оператор края nx.draw(G,with_labels=True) import matplotlib.pyplot as plt plt.show() 

3.2 Направленный график: DiGraph (со стрелкой)
Единственное различие между этой программой и программой в 2.1 состоит в том, что неориентированный Graph Изменен на направленный DiGraph
Сравните следующее изображение с предыдущим.

# step1: Создайте пустое изображение import networkx as nx G=nx.DiGraph() # Создать пустое изображение без ничего # step2: Добавить ребра в пустой граф выше start=[1,3,5,7]#Edge start list to=[2,4,6,8]# Боковой конец списка for j in range(len(start)): G.add_edge(start[j], to[j]) nx.draw(G,with_labels=True) import matplotlib.pyplot as plt plt.show() 

4. Построение различных графиков (с весами)

4.1 Графики без направления и веса
Вот несколько отличий от предыдущих:
(1) двусторонний оператор G.add_edge(start[j], to[j]) Будет изменено на G.add_weighted_edges_from()
(2) Толщина края на рисунке указана так: nx.draw(G, width=[float(v[‘weight’]) for (r, c, v) in G.edges(data=True)]) ,один из нихwidthНастройка веса края

# step1: Создайте пустое изображение import networkx as nx G=nx.Graph() # Создать пустое изображение без ничего # step2: Добавить ребра в пустой граф выше start=[1,3,5,7,9,1]#Edge start list to=[2,4,6,8,10,3]# Боковой конец списка value=[0.1,1,10,15,5,6] # Весовой лист края for j in range(0, len(start)): G.add_weighted_edges_from([(start[j], to[j], value[j])]) # Начальная точка, конечная точка, вес кромки # step3: Укажите выходные данные графика: толщину кромки, размещение узлов и т. д. nx.draw(G, with_labels=True,pos=nx.circular_layout(G), width=[float(v['weight']) for (r, c, v) in G.edges(data=True)]) # Узлы расположены в кольцо, толщина ребра в графе тесно связана с весом ребра import matplotlib.pyplot as plt plt.show() 

4.2 Схема с указанием направления и веса
Разница между этим и 3.1 заключается в том, что неориентированный Graph Изменен на направленный DiGraph

# step1: Создайте пустое изображение import networkx as nx G=nx.DiGraph() # Создать пустое изображение без ничего # step2: Добавить ребра в пустой граф выше start=[1,3,5,7,9,1]# Список начальных точек Edge to=[2,4,6,8,10,3]# Боковой конец списка value=[0.1,1,10,15,5,6] # Весовой лист края for j in range(0, len(start)): G.add_weighted_edges_from([(start[j], to[j], value[j])]) # Начальная точка, конечная точка, вес кромки # nx.draw(G, with_labels=True,pos=nx.circular_layout(G), width=[float(v['weight']) for (r, c, v) in G.edges(data=True)]) # Узлы расположены в кольцо, толщина ребра в графе тесно связана с весом ребра import matplotlib.pyplot as plt plt.show() 

В-пятых, вычислите матрицу смежности на основе данных графа

нота:
(1) Нам нужно указать порядок ввода имен узлов, иначе мы не будем знать, какой узел и какие данные узла представляет каждый элемент выходной матрицы смежности.
Оператор, определяющий порядок имен узлов:

nodeslist=[1,2,3,4,5,6,7,8,9,10]# В этом списке указывается порядок имен узлов for node in nodeslist: # Прочитать имя узла G.add_node(str(node)) print("nodeslist:", G.nodes()) # Вывести все узлы 

nodeslist: ['1', '2', '3', '4', '5', '6', '7', '8', '9', '10'] 

(2) Предложения для генерации матрицы смежности из графов

a= nx.adjacency_matrix(G) # Этот оператор выводит конкретные узлы в графе G, которые соединены попарно, и веса их связанных ребер. A=a.todense() # Это предложение предназначено для создания матрицы смежности 

советы: элемент Aij в матрице смежности A представляет: вес всех ребер, переданных от узла i к узлу j, поэтому Aij и Aji не обязательно совпадают

Ниже приведен полный код для создания матрицы смежности:

# step1: Создайте пустое изображение import networkx as nx G=nx.DiGraph() # Создать пустое изображение без ничего nodeslist=[1,2,3,4,5,6,7,8,9,10]# Это матрица порядка имен узлов for node in nodeslist: # Прочитать имя узла G.add_node(node) print("nodeslist:", G.nodes()) # Вывести все узлы # step2: Добавить ребра в пустой граф выше start= [1,3,5,7,9,1]# Список начальных точек Edge to= [2,4,6,8,10,3]# Боковой конец списка value=[0.1,1,10,15,5,6] # Весовой лист края for j in range(0, len(start)): G.add_weighted_edges_from([(start[j], to[j], value[j])]) # Начальная точка, конечная точка, вес кромки # nx.draw(G, with_labels=True,pos=nx.circular_layout(G), width=[float(v['weight']) for (r, c, v) in G.edges(data=True)]) # Узлы расположены в кольце, и толщина ребра в графе тесно связана с весом ребра import matplotlib.pyplot as plt plt.show() # Создать матрицу смежности ниже a= nx.adjacency_matrix(G) print(a) A=a.todense() print(A) # Экспортировать созданную выше матрицу A весов соединений в файл csv import numpy numpy.savetxt('correlation_matrix.csv',A, delimiter = ',') 

Ниже приводится матричный вывод:

— вывод изображения:

Источник

Вывести матрицу смежности графа заданного ребрами вершина-вершина

Простой неориентированный граф задан списком ребер, выведите его представление в виде матрицы смежности.

Выходные данные
Выведите матрицу смежности заданного графа.

Примеры
входные данные
5 3
1 3
2 3
2 5
выходные данные
0 0 1 0 0
0 0 1 0 1
1 1 0 0 0
0 0 0 0 0
0 1 0 0 0

Вывести матрицу смежности графа, заданного ребрами вершина-вершина
Простой неориентированный граф задан списком ребер, выведите его представление в виде матрицы.

Составить матрицу расстояний вершина–дуга для ориентированного графа на С++
Помогите написать функцию которая посчитает эту матрицу! Нужно найти главную медиану графа для.

Лишняя вершина в матрице смежности
При генерации матрицы смежности в стринггриде всегда есть поле и строка под номером 6, которые не.

Вывести матрицу смежности и список смежности графа
Всем привет!! Уважаемые форумчане, помогите плиз с заданием! Я написала код в Си по которому.

Сообщение было отмечено Dark_Fail как решение

Решение

n, m = map(int, input().split()) adj = [[0]*n for _ in range(n)] for it in range(m): r, c = map(int, input().split()) adj[r-1][c-1] = adj[c-1][r-1] = 1 print(adj)

Источник

работа с графами в Python

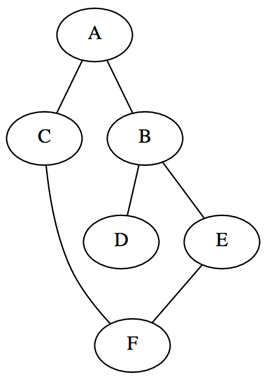
Будет использоваться ненаправленный связный граф V=6 E=6. Существует две популярные методики представления графов: матрица смежности (эффективна с плотными графами) и список связей (эффективно с разряженными графами). Будем использовать второй способ.

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']>

2 Depth-First Search — Поиск вглубину

Алгоритм поиска вглубину: исследуем сначала все возможные вершины (из выбранного корня) доступные из текущей, прежде чем возвращаться назад. Данный алгоритм можно реализовать как рекурсивно, так и итеративно. Последовательность действий:

• Помечаем текущую вершину как посещённую
• Исследуем каждую соседнюю вершину не включённую в список уже посещённых
• Вариант с DFS and BFS in Python (модифицированный, т.к. set не поддерживает упорядоченность элементов)

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def dfs(graph, start): visited, stack = [], [start] while stack: vertex = stack.pop() if vertex not in visited: visited.append(vertex) stack.extend(set(graph[vertex]) - set(visited)) return visited print(dfs(graph, 'A'))

• Вариант с DFS and BFS graph traversal (Python recipe) (модифицированный, т.к. для реализации стека нам необходимо добавлять элементы в конец списка, а не в начало)

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def iteractive_dfs(graph, start, path=None): """iterative depth first search from start""" if path is None: path = [] q = [start] while q: v = q.pop() if v not in path: path = path + [v] q += graph[v] return path print(iteractive_dfs(graph, 'A'))

3 DFS Paths — поиск пути между двумя вершинами

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def dfs_paths(graph, start, goal): stack = [(start, [start])] # (vertex, path) while stack: (vertex, path) = stack.pop() for next in set(graph[vertex]) - set(path): if next == goal: yield path + [next] else: stack.append((next, path + [next])) print(list(dfs_paths(graph, 'A', 'F')))

4 Bread-Firsth Search — Поиск вширину

Позволяет найти кратчайший путь между двумя вершинами. Довольно сложно реализовать рекурсивно, гораздо проще реализовать его с использованием очереди.

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> from queue import deque def bfs(graph, start): visited, queue = [], deque([start]) while queue: vertex = queue.pop() if vertex not in visited: visited.append(vertex) queue.extendleft(set(graph[vertex]) - set(visited)) return visited print(bfs(graph, 'A'))

5 BFS Paths

from queue import deque graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def bfs_paths(graph, start, goal): queue = deque([(start, [start])]) while queue: (vertex, path) = queue.pop() for next in set(graph[vertex]) - set(path): if next == goal: yield path + [next] else: queue.appendleft((next, path+[next])) print(list(bfs_paths(graph, 'A', 'F'))) def shortest_path(graph, start, goal): try: return next(bfs_paths(graph, start, goal)) except StopIteration: return None print(shortest_path(graph, 'A', 'F')) print(shortest_path(graph, 'E', 'D')) print(shortest_path(graph, 'A', 'D')) print(shortest_path(graph, 'F', 'D'))

[['A', 'C', 'F'], ['A', 'B', 'E', 'F']] ['A', 'C', 'F'] ['E', 'B', 'D'] ['A', 'B', 'D'] ['F', 'E', 'B', 'D']

Created: 2017-11-09 Thu 19:40

Источник