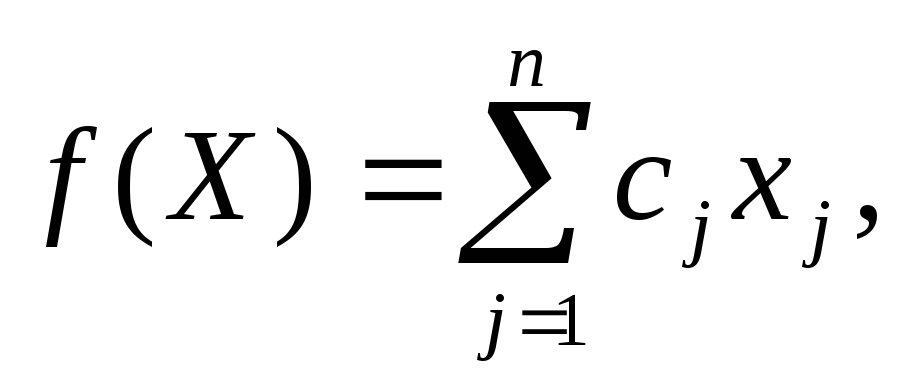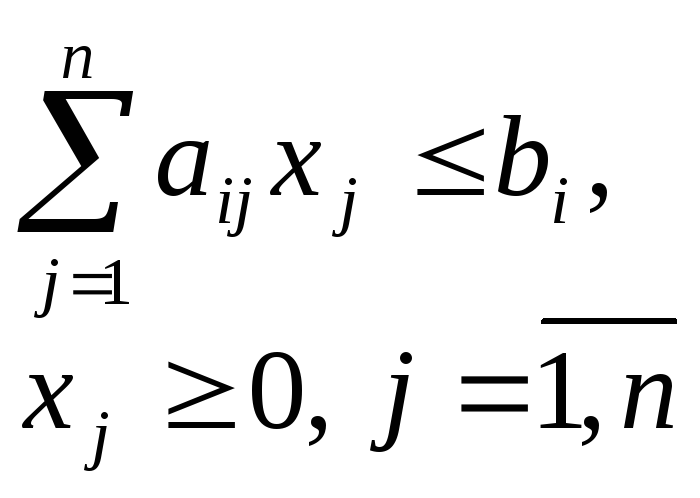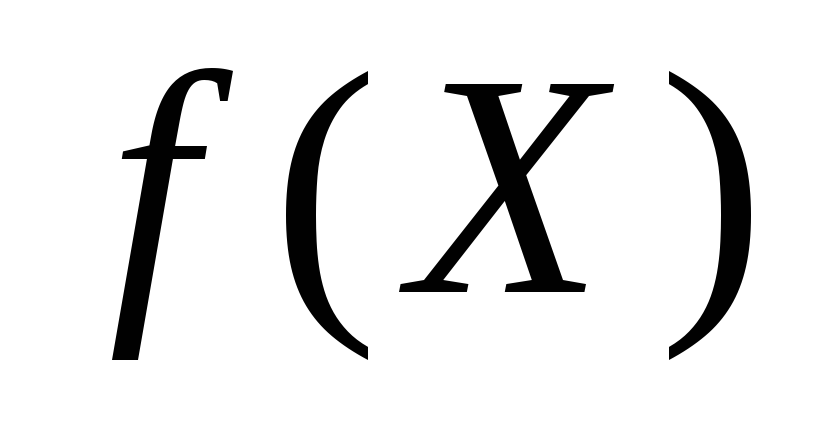Постановка задачи линейного программирования контрольная работа

Линейное программирование

Определение пределов изменения коэффициентов при небазисных переменных в выражении целевой функции. Построение системы неравенств, описывающей оптимальную область изменений коэффициентов при базисных переменных. Оптимальное решение двойственной задачи.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Контрольная работа № 1 по дисциплине

«Автоматизированные информационно-управляющие системы»

1. Сформулировать по заданному 24-хзначному числу задачу линейного программирования вида:

где все параметры модели должны быть определены на основе таблиц 3, 4, 5, а также из следующих условий:

a₁₂

с₂

2. Придумать оригинальную содержательную постановку задачи, которой соответствует модель из п.1.

3. Найти оптимальное решение модели, сформированной в п.1.

4. Произвести анализ на чувствительность модели, сформированной в п.1.

4.1. Определить, в каких пределах могут меняться коэффициенты при небазисных переменных в выражении для целевой функции, не нарушая оптимальности прежнего базиса.

4.2. То же, что и п.4.1, но только для базисных переменных.

4.3. Записать систему неравенств, описывающую допустимую в смысле сохранения оптимальности прежнего решения, область одновременных изменений коэффициентов при базисных переменных в выражении для целевой функции. Построить эту область графически.

4.4. Найти пределы, в которых могут меняться константы в правых частях соотношений в п.1, не нарушая оптимальности прежнего решения.

4.5. Пусть в правых частях первых двух ограничений в п.1 константы b₁ и b₂ могут одновременно быть изменены. Найти систему неравенств, при выполнении которой прежнее решение остается оптимальным. Изобразить допустимую область графически.

5. Двойственная задача.

5.1. Записать для задачи, сформированной в п.1, двойственную задачу.

5.2. Найти оптимальное решение двойственной задачи.

5.3. Используя двойственную модель определить, в каких интервалах могут меняться коэффициенты при небазисных переменных в выражении для целевой функции, не нарушая оптимальности прежнего решения.

5.4. Пусть вводятся новые управляемые переменные x₁₀ и x₁₁. Коэффициенты при x₁₀ и x₁₁ записаны в табл.6. Целесообразен ли ввод данных переменных? двойственный задача коэффициент переменная

Источник

Контрольная работа

Составитель: старший преподаватель кафедры математики Трухина Л. И.

Рекомендовано к печати кафедрой математики

Протокол заседания № 5 от 29 января 2014 г.

Линейные модели являются одним из наиболее активно используемых классов математических моделей. Они сравнительно просты, хорошо разработаны, допускают полное исследование и достаточно эффективны в целом ряде стандартных ситуаций.

Линейное программирование – это математический метод решения задачи оптимального распределения имеющихся ресурсов (денег, материалов, времени) для достижения определённой цели (наибольшего дохода или наименьших издержек). Программированиев данном термине имеет смыслпланирования.Линейноеозначает, что ищется экстремум линейной целевой функции при линейных ограничениях (линейных уравнениях или линейных неравенствах).

Общие ситуации, в которых линейное программирование применяется часто и эффективно:

задачи о составлении смеси, цель которых заключается в выборе наиболее экономичной смеси ингредиентов (руды, нефти, пищевых продуктов и др.) при учёте ограничений на физический или химический состав смеси и на наличие необходимых материалов;

задачи производства, целью которых является подбор наиболее выгодной производственной программы выпуска одного или нескольких видов продукции при использовании некоторого числа ограниченных источников сырья;

задачи распределения, цель которых состоит в том, чтобы организовать доставку материалов от некоторого числа источников к некоторому числу потребителей так, чтобы оказались минимальными либо расходы по этой доставке, либо время затрачиваемое на неё, либо некоторая комбинация того и другого. В простейшем виде это задача о перевозках (транспортная задача).

Наиболее распространённым методом решения задачи линейного программирования является симплекс-метод. В простейшем случае, когда число переменных равно двум, удобен простой и наглядныйграфический метод.

1. Общая задача линейного программирования

Задача линейного программирования состоит в составлении плана максимизирующего или минимизирующего некую линейную функцию при ограничениях в виде линейных уравнений или линейных неравенств:

найти вектор , максимизирующий (минимизирующий) функцию

(1)

и удовлетворяющий условиям

(2)

Линейная функция называетсяцелевой функциейзадачи. Условия (2) называются ограничениями задачи.

Любое решение системы ограничений ЗЛП называется допустимымпланом.

Допустимый план, максимизирующий или минимизирующий целевую функцию называется оптимальным.

План, у которого отличным от нуля компонентам соответствует система линейно независимых векторов, называется опорным планом.

Теорема.Множество планов задачи линейного программирования является выпуклым множеством.

Теорема.Оптимальный план задачи линейного программирования находится в крайней точке выпуклого множества планов. Если оптимальный план находится в двух крайних точках выпуклого множества планов, то он находится также и в любой точке, являющейся выпуклой комбинацией этих крайних точек.

Источник

Пример постановки задачи линейного программирования

Акционерное общество производит и реализует оптовыми партиями соответственно по цене 45 руб. и 30 руб. книги и настольные календари. Постоянные затраты общества (управленческие расходы, содержание офиса и т.п.) составляют 202200 руб. в квартал, переменные затраты (стоимость бумаги, услуги типографии и т.п.) – соответственно 15.75 руб. и 12.3 руб. в расчете на одну книгу и один календарь. Налог на добавленную стоимость составляет 16.67 % цены изделия.

Опыт реализации изделий в предыдущие плановые периоды показал, что в течение квартала можно реализовать не более 100000 книг и 40000 календарей.

Требуется на планируемый квартал определить объем производства и реализации изделий (структуру производства и реализации), при котором общество получит максимальную прибыль, а суммарные затраты на производство и реализацию изделий не будут превосходить 2000000 руб.

Формирование математической модели

Ввод условий задачи:

Сформировать таблицу в диапазоне ячеек a1:f11, приведенную на рис. 1.

Рис. 1. Таблица для ввода условий задачи линейного программирования

1. В ячейку D6 ввести формулу =СУММПРОИЗВ(B$3:C$3;B6:C6).
2. В ячейку D9 ввести формулу =СУММПРОИЗВ(B$3:C$3;B9:C9) и размножить по столбцу в ячейках D10 и D11.

1. Решение задачи

   

   1. В меню выбрать «Сервис — Поиск решения». В поле «Установить целевую ячейку:» набрать $D$6. В поле «Равной:» установить маркер в «Максимальному значению».
   2. В поле «Изменяя ячейки» ввести $B$3:$C$3.
   3. Установить курсор-прямоугольник в поле «Ограничения». Нажать на кнопку «Добавить». В поле «Ссылка на ячейку:» ввести $B$3. Выбрать знак >=. В поле «Ограничение» ввести =$B$4. Нажать кнопку «Добавить».
   4. В поле «Ссылка на ячейку:» ввести $С$3. Выбрать знак >=. В поле «Ограничение» ввести =$С$4. Нажать кнопку «Добавить».
   5. В поле «Ссылка на ячейку:» ввести $D$9. Выбрать знак
   6. В поле «Ссылка на ячейку:» ввести $D$10. Выбрать знак
   7. В поле «Ссылка на ячейку:» ввести $D$11. Выбрать знак

Рис. 2. Диалоговое окно Поиск решения

Источник