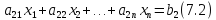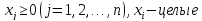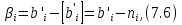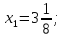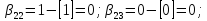Глава 3. Целочисленное линейное программирование.
Важное значение в ЛП имеет случай, когда неизвестные целочисленные.Задача ЛП с дополнительным условием целочисленности неизвестных исследуется в новойобласти математического программирования – целочисленном (дискретном) программировании (ЛЦП).
§1 Метод Гомори
К основной задаче ЛП добавим дополнительное условие – условие целочисленности неизвестных, в результате получим задачу ЛЦП. Можно, конечно, получить дробное оптимальное решение задачи ЛП и его округлить до ближайших целых значений. Но тогда может случиться, что мы будем либо близки к оптимальному плану задачи ЛЦП, либо далеки, либо вообще уйдем за пределы множества планов ЛЦП.Один из возможных методов решения задачи ЛЦП – метод Гомори.Идея метода базируется на представлении вещественного числа в виде суммы его целой и дробной частей.Как известно, целой частью вещественного числа «а» называется наибольшее целое число, не превосходящее
Обозначение целой части[a].Разность
есть дробная часть числа
Очевидно, например, что
и
Например:
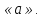
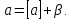
Рассмотрим метод Гомори на примере (общая задача ЛП):
План задачи линейного программирования называют целочисленным, если все его составляющие целые числа.
Для определения целочисленного решения задачи:
можно использовать алгоритм Гомори, состоящий из следующих этапов.
Первый этап. Задача (7.1) — (7.3) решается симплекс-методом до получения оптимального плана.
Второй этап.В последнюю симплекс-таблицу, содержащую оптимальный план, добавляют ограничение
составленное для i- ой строки следующим образом:
(Символом [a] обозначают целую часть числаa, то есть наибольшее целое число, не превосходящееa).
Третий этап.В последней симплекс-таблицевыбирают введенную строку разрешающей.Разрешающий столбец выбирают по правилу двойственного симплекс-метода. С выбранным таким образом разрешающим элементом осуществляют переход по известному алгоритму к следующей симплекс-таблице. Если при этом полученное решение окажется еще не целочисленным, то общий шаг повторяют.
1. Признаком отсутствия целочисленного решения в задаче (7.1)-(7.4) служит появление хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами. То есть в этом случае соответствующее уравнение не имеет решения в целых числах.
2. Дополнительное ограничение целесообразно составлять для строки, содержащей в столбце свободных членов наибольшую дробную часть.
3. Дополнительное ограничение можно составлять несколько иначе, то есть в качестве коэффициентов при неизвестных выбрать единицы. Тем самым получим ограничение в виде
.
Схема решения задачи (7.1) – (7.4)
- Исходную задачу решают симплекс-методом до получения оптимального решения без учета требования целочисленности его.
- Составляют дополнительное ограничение для строки, содержащую наибольшую дробную часть в столбце свободных членов.
- Коэффициенты нового ограничения вносят в последнюю симплекс-таблицу.
- Введенную строку выбирают разрешающей.
- Разрешающий элемент выбирают по принципу двойственного симплекс-метода.
- С выбранным таким образом разрешающим элементом осуществляют переход (по известным правилам) к следующей симплекс-таблице.
- В случае необходимости составляют еще одно дополнительное ограничение и процесс повторяют до получения целочисленного решения.
Пример.
(1) Отбросим пока условие целочисленности (*) и решим задачу ЛП
(2) Задача ЛП – каноническая. Исходная таблица
| B | Свободный член | Коэффициенты при неизвестных | |||
 |  |  |  | ||
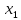 | 15 |  |  |  |  |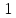
 |  |  |  |  |  |
 |  |  |  |  |  |
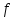Итерация 1
| B | Свободный член | Коэффициенты при неизвестных | |||
 |  |  |  | ||
 |  |  |  |  | |
 |  |  |  |  | |
 |  |  |  | ||
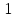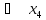Итерация 2
| B | Свободный член | Коэффициенты при неизвестных | |||
 |  |  |  | ||
 |  |  |  |  | |
 |  |  |  |  | |
 |  |  |  | ||
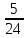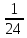План: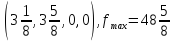 
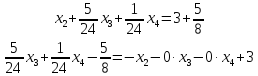
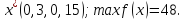
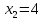
оказался нецелочисленным.Для отыскания целочисленного плана применим метод Гомори (метод отсечений). С этой целью из завершающей симплексной таблицы выпишем каноническую систему (3) (эквивалентная системе (2)): 
(3) Свободные члены обоих уравнений дробные. Выбираем первое уравнение (с наибольшим дробным свободным членом):
Рассмотрим неравенство (т. н. неравенство Гомори) 
(3)* Запишем (с положительным свободным членом) 
. (3)** В [4, с. 173] показано, что любой целочисленный план задачи (2) удовлетворяет и неравенству (3)*. Оптимальный же (нецелочисленный) план задачи (2) не удовлетворяет неравенству (3)*. Добавим неравенство (3)** к условиям задачи (2), то есть: 
, а т.к. системы были эквивалентны, то задача ЛЦП запишется ((3) +(3)** ):
(4) Задача (4) почти каноническая (
=1,2,3….). Решая задачу, получим оптимальный план 
Замечание 1. Ясно, что всякое дополнительное ограничение сужает область допустимых значений и максимум может быть только меньше или равен, но никак не больше. Оптимальный нецелочисленный план при этом отсекается. Если бы при решении задачи (4) план получился бы нецелочисленным, то необходимо вновь выписать неравенство Гомори к канонической системе из последней симплексной таблицы (новой) и далее вновь решать задачу ЛП и т.д., пока план оптимальной не окажется целочисленным. Замечание 2. Если левая часть уравнения системы имеет дробные часть равные 0, а правая часть дробная, то задача ЛЦП планов не имеет, например
. Здесь при целых значениях неизвестных никак не получится дробь 
, т.е. неизвестные нецелочисленны, поэтому для составления неравенства Гомори берем уравнения с дробной левой частью.Замечание 3. Ранее, когда решали задачу ЛП оптимальный план был: 
. Сейчас получили 
. Если бы не применили для решения задачи ЛЦП метод Гомори, а просто округлили бы, глядя на решение задачи ЛП, например, 
,
; или
или
,
то эти планы вообще выходят за пределы множества планов, т.к. не удовлетворяют системе задачи (1), в частности, системе 
Ну, а если округлить 
,
, то хотя это и план, ноf(x) = 39, а у нас
, т.е. значенияf(x) значительно отличаются. Пример.Найти 
при условиях: 
Снимем условие целочисленности. MaxZ=x1 + 2×2 при условиях: x1— 2x2+x3 = 2 — 2x1+x2+x4=2 x1+x2+x5=3 
. Исходная симплексная таблица
Базисные переменные  | Свободные члены ( ) | Коэффициенты при неизвестных | ||||
 |  |  |  |  | ||
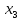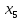 | 2 | 1 | -2 | 1 | ||
 | 2 | -2 | 1 | 1 | ||
 | 3 | 1 | 1 | 1 | ||
| Z | 0 | -1 | -2 | |||
Итерация 1
Базисные переменные  | Свободные члены ( ) | Коэффициенты при неизвестных | ||||
 |  |  |  |  | ||
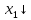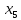 | 6 | -3 | 1 | 2 | ||
 | 2 | -2 | 1 | 1 | ||
 | 1 | 3 | -1 | 1 | ||
| Z | 4 | -5 | 2 | |||
Итерация 2
Базисные переменные 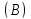 | Свободные члены (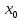 ) | Коэффициенты при неизвестных | ||||
 |  |  |  |  | ||
 | 7 | 1 | 1 | 1 | ||
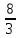 |  | 1 |  |  | ||
 |  | 1 |  |  | ||
| Z |  = 5  |  |  | |||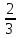
Задача ЛП решена. Решение нецелочиcленное. В таблице (7.3) получен оптимальный план. В столбце 
не все элементы целые. Так как во второй строке в
содержится наибольшая дробная часть, то для нее составляют дополнительное ограничение, коэффициенты которого следующие: 
или 
Добавляем неравенство Гомори к итерации 2. Получим задачу ЦЛП: MaxZ=x1 + 2x2 при условиях: x3 +x4+x5 = 7 x2+
x4+
x5 = 
x1—
x4+
x5= 
— 
x4—
x5 ≤
. 
. Исходная симплексная таблица
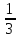
Базисные переменные  | Свободные члены ( ) | Коэффициенты при неизвестных | |||||
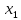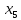 |  |  |  |  | S2 | ||
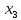 | 7 | 1 | 1 | 1 | |||
 |  | 1 |  |  | |||
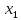 |  | 1 |  |  | |||
 S2 |  |  |  | 1 | |||
| Z |  = 5  |  |  | ||||
Итерация 1
Базисные переменные  | Свободные члены ( ) | Коэффициенты при неизвестных | S2 | |||||
 |  |  |  |  | ||||
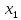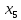 | 5 | 1 | -1 | 3 | ||||
 | 2 | 1 | 1 | |||||
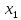 | 1 | 1 |  | -1 | ||||
| S2 | 2 | 1 | 2 | -3 | ||||
| Z | 5 | 1 | 1 | |||||
Получили оптимальное и целочисленное решение 
L(max) = 5. Дадим геометрическую интерпретацию решения данной задачи. Из рис. 1 видно, что максимально значение целевая функция принимает в точке 
, то есть решение
является оптимальным, но без учета требования целочисленности. 
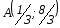
| II |
Рис. 1 С учетом требования целочисленности решение 
не является оптимальным, поэтому используем дополнительное ограничение 
или 
. Значения переменных x4 и x5 подставим из второго и третьего уравнений системы ограничений
,
. В результате получим
. Этому неравенству на рис. 1 соответствует полуплоскость, ограниченная прямой
, отсекающей от многоугольника допустимых решений треугольник АДА*. В новом многоугольнике допустимых решений ОДА*ВС найдем точку А*(1,2), в которой целевая функция принимает максимальное значение. Так как координаты точки А* – целые числа, то решение
является оптимальным планом исходной задачи.
Научная электронная библиотека
Под задачей целочисленного линейного программирования (ЦЛП) понимается задача линейного программирования, в которой некоторые (а возможно, и все) переменные должны принимать целые значения. Задача ЦЛП называется полностью целочисленной, если все её переменные должны быть целочисленными. Для смешанной задачи ЦЛП лишь некоторые переменные предполагаются целочисленными, а остальные могут принимать произвольные (нецелые) значения.
Задачу ЦЛП можно решить, например, как задачу ЛП без учёта условий целочисленности переменных, а затем округлить полученное решение. Использование такого подхода требует проверки допустимости полученного решения. Таким методом часто пользуются при решении практических задач, особенно когда значения переменных настолько велики, что можно пренебречь ошибками округления. Однако при решении задач, в которых целочисленные переменные принимают малые значения, округление может привести к далёкому от истинного оптимума целочисленному решению. Кроме того, при решении задач большой размерности такой метод требует слишком много машинного времени. Например, пусть оптимальное решение соответствующей задачи ЛП имеет вид x1 = 2,4; x2 = 3,5 . Для получения приближённого оптимального решения необходимо рассмотреть четыре точки (2;3); (2;4); (3;3); (3;4) и выбрать среди них допустимую точку с наилучшими значениями целевой функции. Если в задаче имеются 10 целочисленных переменных, то следует рассмотреть 2 10 = 1024 варианта целочисленного решения. Но даже рассмотрение всех вариантов не гарантирует получения оптимального целочисленного решения задачи.
Одним из методов решения как полностью целочисленных, так и смешанных задач ЦЛП является метод ветвей и границ. Он представляет собой эффективную процедуру перебора всех целочисленных допустимых решений.
Удобно представить последовательность задач ЛП, возникающих при использовании процедуры метода ветвей и границ, в виде сети или дерева. Они состоят из множества вершин и соединяющих их дуг или ветвей. Каждая вершина представляет собой либо начальную, либо конечную точку некоторой ветви. В том случае, если в некоторой вершине возникает ситуация, когда исследуемое решение является оптимальным и целочисленным или, наоборот, решение отсутствует, то нет необходимости производить дальнейшее ветвление, поэтому рассматриваемая вершина является прозондированной.
Для определения переменной, по которой производится начальное ветвление, разработан ряд правил.
- 1. Выбор целочисленной переменной, значение которой в оптимальном решении ЛП-1 имеет наибольшее дробное значение.
- 2. Приоритетной является переменная, коэффициент которой в целевой функции превосходит остальные.
- 3. Выбор переменной с наименьшим номером.
Для дальнейшего ветвления выбираются следующие вершины.
- Следует выбирать вершину, соответствующую наибольшему оптимальному значению целевой функции.
- Произвольным образом выбирается задача ЛП, решавшаяся последней.
Промежуточная вершина является прозондированной в том случае, если она удовлетворяет хотя бы одному из следующих условий
- 1. Оптимальное решение, соответствующее данной вершине целочисленно.
- 2. Задача ЛП, соответствующая рассмотренной вершине, не имеет допустимых решений.
- 3. Оптимальное значение f (x) соответствующей задачи ЛП не превосходит текущей нижней границы.
При использовании метода ветвей и границ выбор вершины для дальнейшего ветвления происходит до тех пор, пока остаётся хотя бы одна не прозондированная вершина. Прозондированная вершина с наилучшим значением f (x) даёт оптимальное решение исходной задачи ЦЛП. Получение перед реализацией метода ветвей и границ допустимого целочисленного решения задачи ЦЛП может оказаться весьма полезным, так как оно даёт начальную нижнюю границу, используемую до получения лучшей нижней границы по методу ветвей и границ.
Анализ опыта решения практических задач привёл к выработке ряда рекомендаций который можно использовать для уменьшения времени вычислений.
- 1. Количество целочисленных переменных следует уменьшить насколько возможно. Например, целочисленные переменные, значения которых должны быть не меньше 20, можно рассматривать как непрерывные.
- 2. Добавление новых ограничений, особенно включающих целочисленные переменные, обычно уменьшает время решения задач ЦЛП.
- 3. По возможности следует получать близкие друг к другу верхнюю и нижнюю границы значений целочисленных переменных.
- 4. Можно заканчивать реализацию метода ветвей и границ, если для задач максимизации выполняется соотношение:
- 5. Рекомендуется выбирать для ветвления целочисленные переменные в порядке убывания их приоритета, назначаемого в соответствии с технико — экономической интерпретацией переменных и опытом пользователя.
В задачах с большим количеством переменных более эффективным является метод отсечения Гомори, который основан на введении дополнительных условий и анализе значений базисных и небазисных переменных, т. е. выполняется модифицированный симплекс-метод. Кроме того, данный метод может применяться в параметрическом программировании, когда исходные данные (коэффициенты) в ЦФ и ограничениях являются не постоянными величинами, а функциями, зависящими определенным образом от некоторых параметров.