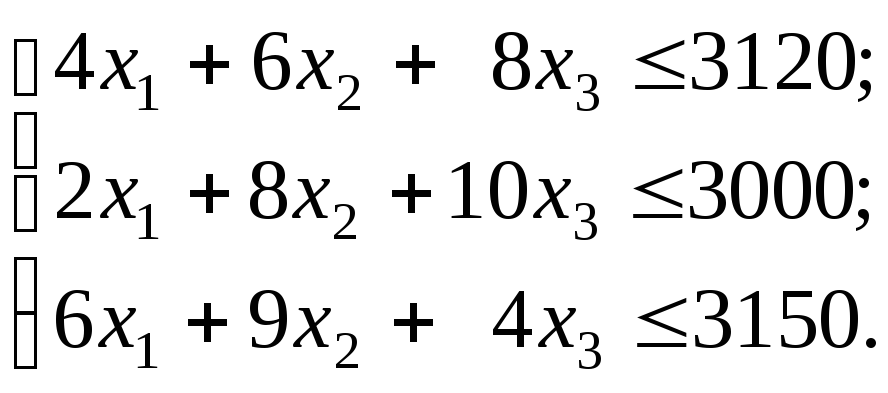Поиск решения при решении задачи линейного программирования

Решение задач линейного программирования средствами программы Excel

Цель работы:изучение современных программных средств решения задачи линейного программирования; практическое решение задач линейного программирования графическим методом, симплекс-методом и средствами программыMicrosoftExcel; программная реализация симплекс-метода на языке программирования высокого уровня.

1. Теоретическая часть

Для решения задач линейного программирования в программе Microsoft Excel имеется надстройка Поиск решения, обращение к которой производится из меню Сервис.

Если команда Поиск решения отсутствует в меню Сервис, то требуется установить надстройку «Поиск решения». Для этого в меню Сервис выбирается команда Надстройки, которая открывает диалоговое окно, показанное на рис. 1.

Далее в этом окне устанавливается флажок той надстройки, которую необходимо загрузить, и нажимается кнопка OK.

Покажем использование надстройки «Поиск решения» на примере решения следующей задачи.

Постановка задачи

Предприятие изготавливает и реализует три вида продукции – P₁, Р₂ и Р₃. Для производства продукции используются три вида ресурсов – комплектующие изделия, сырье и материалы. Запасы ресурсов и их расход на изготовление единицы продукции каждого вида приведены в табл. 1.

Расходы ресурсов на 1 ед. продукции

Прибыль от реализации единицы продукции каждого вида составляет 240, 210 и 180 денежных единиц для P₁, Р₂ и Р₃ соответственно.

Требуется определить производственную программу предприятия таким образом, чтобы прибыль от реализации продукции была максимальной.

Математическая модель задачи

Обозначим переменными x₁, x₂ и x₃ искомые объемы производства продукции видов P₁, Р₂ и Р₂, а через F – прибыль предприятия. Тогда математическая постановка представленной задачи принимает следующий вид.

Определить значения переменных x₁, x₂ и x₃, для которых достигается максимум целевой функции

F = 240 x₁ + 210 х₂ + 180 x₃

Целевая функция описывает суммарную прибыль от реализации произведенной продукции всех трех видов. Ограничения (1), (2) и (3) учитывают расход и запасы комплектующих изделий, сырья и материалов соответственно. Поскольку объемы производства продукции не могут быть отрицательными, добавляются условия

Порядок оптимального решения задачи

Примерные действия, необходимые для решения задачи линейного программирования средствами программы Excel, представим в виде последовательности шагов.

Шаг 1. Исходные данные задачи записываются на рабочем листе электронной таблицы. Один из вариантов показан на рис. 2.

Замечание. Если известно исходное допустимое базисное решение, то можно несколько ускорить процесс поиска оптимального решения. Для этого начальные значения некоторых или всех переменных могут быть заданы вручную. В данном примере для их хранения используются ячейки $B$2, $C$2 и $D$2. Если допустимое базисное решение не задано, то программа Excel автоматически определяет начальные значения переменных задачи.

Шаг 2. В ячейку E3 вводится формула

для вычисления текущего значения целевой функции, которая находит сумму попарных произведений ячеек (В3:D3) с коэффициентами при переменных в выражении целевой функции на ячейки ($B$2:$D$2) с текущими значениями переменных.

Шаг 3. Чтобы задать ограничения решаемой задачи, в ячейки E5, E6 и E7 копируется формула из ячейки E3. После этого в указанных ячейках должны быть получены формулы, представленные в табл. 2.

Шаг 4. После создания таблицы с исходными данными курсор устанавливается в ячейку E3, содержащую формулу для вычисления целевой функции. Далее в меню Сервис выбирается команда Поиск решения, которая открывает диалоговое окно, приведенное на рис. 3.

В поле Установить целевую ячейку окна «Поиск решения», показанного на рис. 3, должен появиться адрес ячейки с формулой целевой функции (в данном примере это ячейка $E$3).

Затем в этом окне (рис. 3) заполняются следующие поля этого окна:

— в поле Равной переключатель вида экстремума целевой функции устанавливается в положение максимальное значение (или минимальное значение при соответствующей постановке задачи);

— в поле Изменяя ячейки указывается диапазон ячеек со значениями переменных задачи, выделяемый на рабочем листе электронной таблицы (в примере это ячейки $B$2:$D$2);

— в поле Ограничения задаются ограничения исходной задачи. Для этого курсор устанавливается в поле ввода ограничений и нажимается кнопка Добавить. В результате выводится диалоговое окно «Добавление ограничения», показанное на рис. 4.

В этом окне в поле Ссылка на ячейку вводится адрес ячейки с формулой соответствующего ограничения (например, для ограничения (1) это будет ячейка E5), а в поле Ограничение указывается предельное значение, которое может принимать выбранное ограничение (в данном примере правая часть ограничения (1) находится в ячейке G5).

Следует заметить, что заполнение полей Ссылка на ячейку и Ограничение в окне «Добавление ограничения» можно выполнить выделением соответствующих ячеек рабочего листа электронной таблицы.

Затем выбирается вид отношения, связывающего левую и правую части ограничения, что показано на рис. 5.

После нажатия кнопки Добавить в окне «Добавление ограничения» (или кнопки ОК для ввода последнего ограничения) данное ограничение попадает в список ограничений решаемой задачи. С помощью кнопок Удалить и Изменить можно удалять выделенные в списке ограничения или вносить в них исправления.

Замечание. В окне «Добавление ограничения» можно указать, что все или некоторые переменные должны принимать только целые значения (рис. 5). Это позволяет получать решения задач целочисленного линейного программирования (полностью или частично целочисленных).

Шаг 5. После заполнения всех полей окна «Поиск решения» нажимается кнопка Параметры (рис. 3), которая открывает диалоговое окно «Параметры поиска решения», показанное на рис. 6.

В этом окне требуется установить флажки Линейная модель для решения задачи линейного программирования и Неотрицательные значения, если такое условие накладываются на все переменные задачи.

Здесь (рис. 6) также можно определить параметры процесса решения: предельное время поиска решения, максимальное количество итераций, точность и т.п. Флажок Показывать результаты итераций позволяет по шагам следить за поиском решения. Флажок Автоматическое масштабирование включается в том случае, когда разброс значений переменных очень велик.

Шаг 6. Задав необходимые параметры в окне «Параметры поиска решения», следует нажать на кнопку Выполнить для поиска решения задачи (рис. 3) в окне «Поиск решения». Если решение найдено, то на экран выводится окно с соответствующим сообщением (рис. 7).

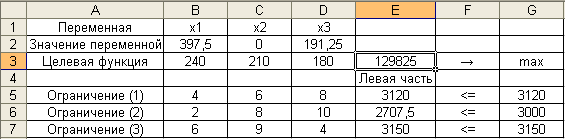
Полученные результаты отображаются на рабочем листе электронной таблицы, как это показано на рис. 8. В частности, значения переменных — в ячейках $B$2:$D$2, значение целевой функции – в ячейке E3.

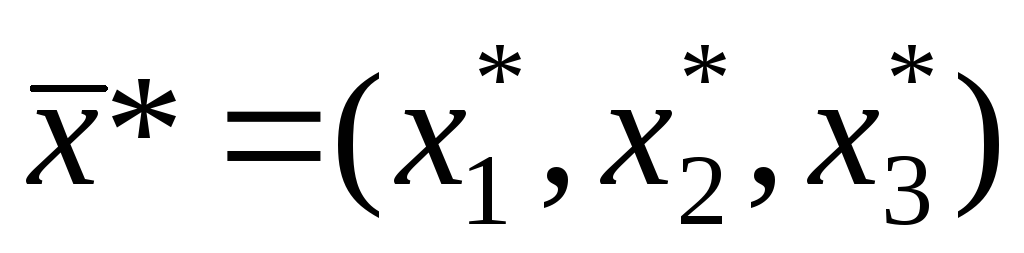
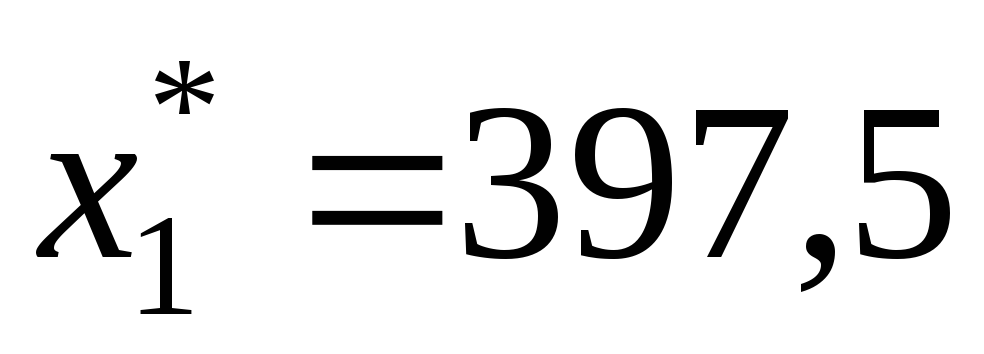
Таким образом, получено оптимальное решение исходной задачи в виде вектора , где,и, для которого значение целевой функцииF максимально и составляет F* = 129825.

Результаты решения задачи линейного программирования также можно сохранить в виде отдельных рабочих листов с именами Отчет по результатам, Отчет по устойчивости и Отчет по пределам. Для сохранения результатов в виде отчетов необходимо предварительно в поле Тип отчета выделить требуемые типы отчетов (рис. 7). В этом же окне можно отказаться от полученных решений и восстановить исходные значения переменных.

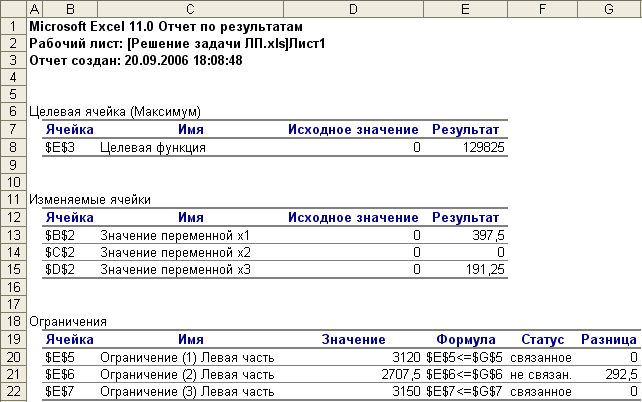
Отчет по результатам для рассмотренной задачи показан на рис. 9.

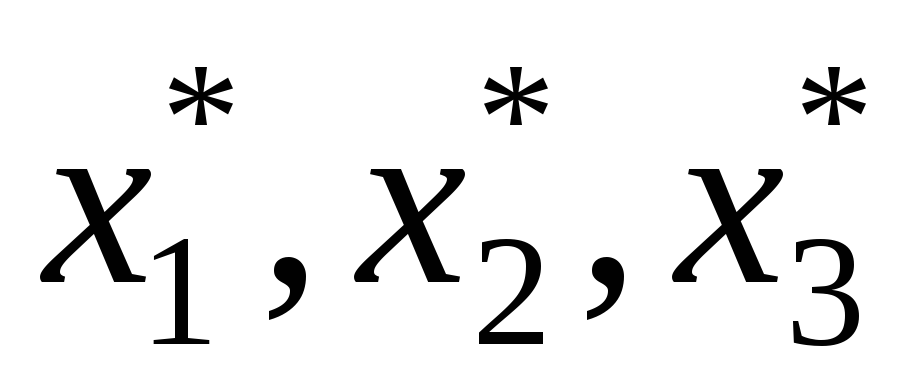
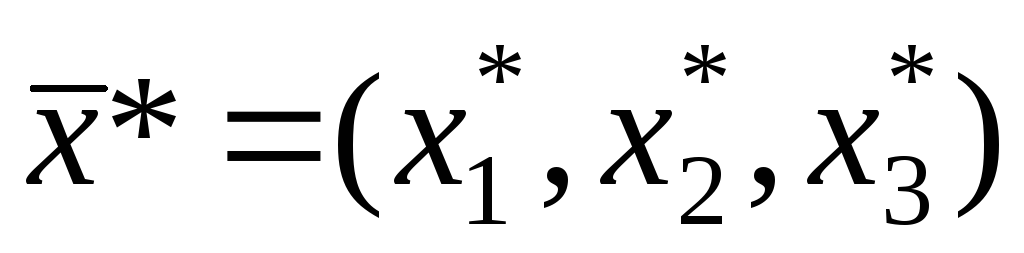
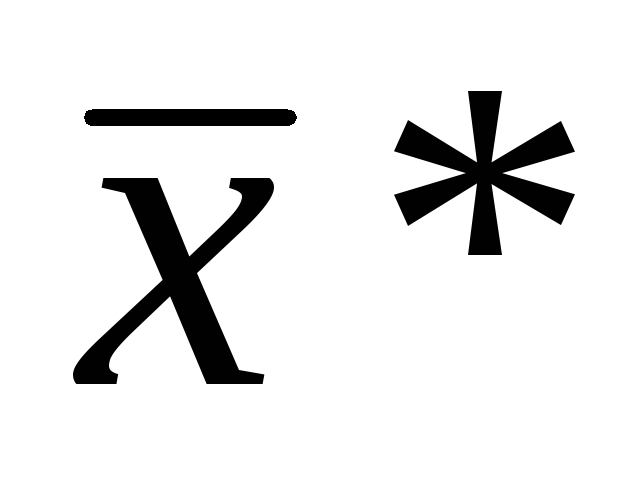
В данном отчете представлены оптимальное решение задачи линейного программирования и его расположение в области допустимых решений. В графах Результат выводятся оптимальные значения целевой функции F* и переменных задачи , а также их значения для исходного базисного решения, с которого начинался поиск оптимального решения (графаИсходное значение). Состояние ограничений (графа Статус) характеризует расположение точки в области допустимых решений. ГрафаРазница показывает разности между значениями левых и правых частей ограничений (невязки). Для связанного ограничения невязка равна нулю, что свидетельствует о расположение точки на границе области допустимых решений, которая задается этим ограничением. Если ограничение являются не связанным, то оно не влияет на оптимальное решение.

Замечание. В экономической интерпретации связанные ограничения соответствуют дефицитным ресурсам. Для не связанных ограничений графа Разница показывает оставшиеся объемы неиспользованных не дефицитных ресурсов. В рассмотренной задаче ограничения (1) и (3) соответствуют комплектующим изделиям и материалам, которые являются дефицитными ресурсами. Ограничение (2) является не связанным, т.е. не влияет на оптимальный план производства продукции по критерию максимальной прибыли. Это означает, что второй ресурс (сырье) не использован в объеме 292,5 ед.

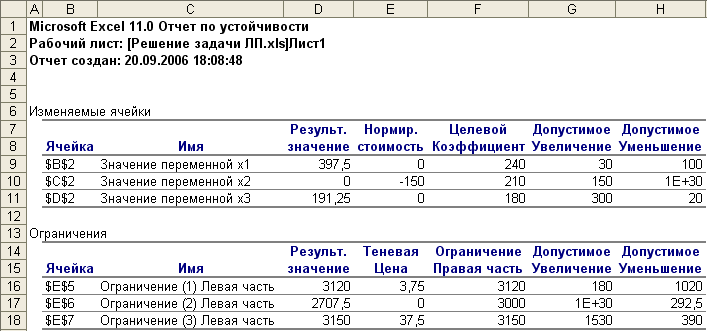
В отчете по устойчивости (рис. 10) приведены границы устойчивости переменных задачи (графы Допустимое увеличение и Допустимое уменьшение коэффициентов целевой функции), а также границы устойчивости теневых цен (т.е. переменных двойственной задачи), в пределах которых оптимальное решение не изменяется. Большие значения пределов (1Е+30) означают фактическое отсутствие соответствующих границ, т.е. переменная может изменяться до бесконечности.

В графе Нормированная стоимость элемент во второй строке (-150) показывает, на сколько уменьшится значение функции, если в решении переменную x₂ увеличить на единицу. С другой стороны, при допустимом увеличении коэффициента функции при неизвестной x₂ на 150 единиц значение этой переменной не изменится, т.е. неизвестная x₂ будет равна нулю, а если выйти за пределы допустимого увеличения (коэффициент при x₂ увеличить более чем на 150), то неизвестная x₂ в решении будет больше нуля.

В отчете по пределам (рис. 11) показаны нижние и верхние пределы возможного изменения переменных (в пределах области допустимых решений) и соответствующие значения целевой функции (графа Целевой результат) при этих изменениях. В частности, если x₁ = 0, а x₂ и x₃ остаются без изменений, то F = 2400 + 2100 + 180191,25 = 34425; при x₃ = 0 и неизменных x₁ и x₂ получим F = 240397,5 + 2100 + 1800 = 95400.

Источник