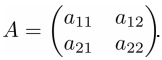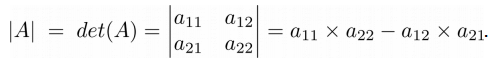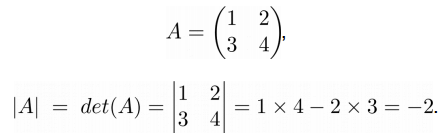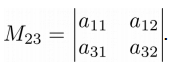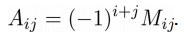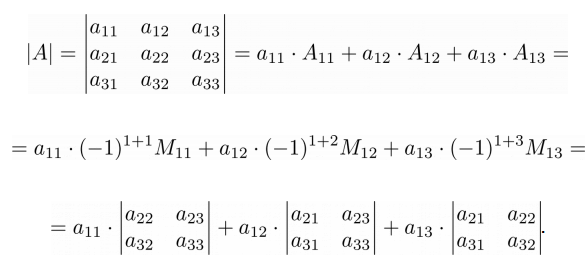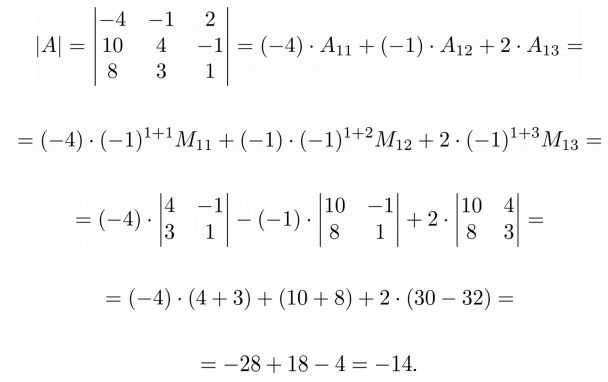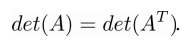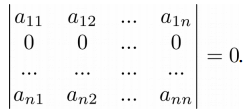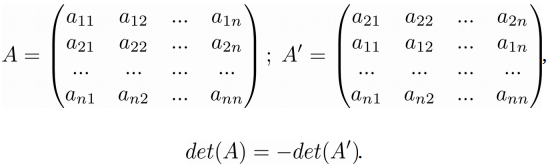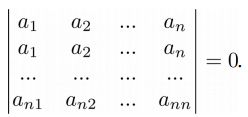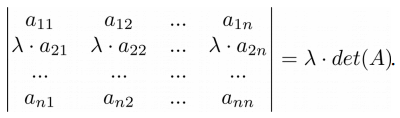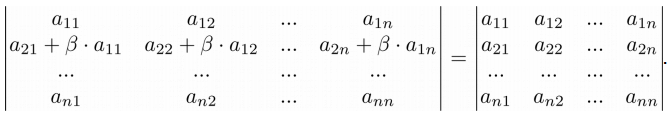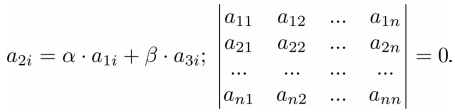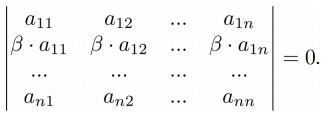- numpy.linalg.det#
- Linear algebra ( numpy.linalg )#
- The @ operator#
- Matrix and vector products#
- Decompositions#
- Matrix eigenvalues#
- Norms and other numbers#
- Solving equations and inverting matrices#
- Exceptions#
- Linear algebra on several matrices at once#
- Линейная алгебра на Python. [Урок 4]. Определитель матрицы
- Определитель матрицы
- P.S.
- NumPy, часть 4: linalg
- Возведение в степень
- Разложения
- Некоторые характеристики матриц
- Системы уравнений
numpy.linalg.det#
Another way to represent the determinant, more suitable for large matrices where underflow/overflow may occur.
Similar function in SciPy.
Broadcasting rules apply, see the numpy.linalg documentation for details.
The determinant is computed via LU factorization using the LAPACK routine z/dgetrf .
The determinant of a 2-D array [[a, b], [c, d]] is ad — bc:
>>> a = np.array([[1, 2], [3, 4]]) >>> np.linalg.det(a) -2.0 # may vary
Computing determinants for a stack of matrices:
>>> a = np.array([ [[1, 2], [3, 4]], [[1, 2], [2, 1]], [[1, 3], [3, 1]] ]) >>> a.shape (3, 2, 2) >>> np.linalg.det(a) array([-2., -3., -8.])
Linear algebra ( numpy.linalg )#
The NumPy linear algebra functions rely on BLAS and LAPACK to provide efficient low level implementations of standard linear algebra algorithms. Those libraries may be provided by NumPy itself using C versions of a subset of their reference implementations but, when possible, highly optimized libraries that take advantage of specialized processor functionality are preferred. Examples of such libraries are OpenBLAS, MKL (TM), and ATLAS. Because those libraries are multithreaded and processor dependent, environmental variables and external packages such as threadpoolctl may be needed to control the number of threads or specify the processor architecture.
The SciPy library also contains a linalg submodule, and there is overlap in the functionality provided by the SciPy and NumPy submodules. SciPy contains functions not found in numpy.linalg , such as functions related to LU decomposition and the Schur decomposition, multiple ways of calculating the pseudoinverse, and matrix transcendentals such as the matrix logarithm. Some functions that exist in both have augmented functionality in scipy.linalg . For example, scipy.linalg.eig can take a second matrix argument for solving generalized eigenvalue problems. Some functions in NumPy, however, have more flexible broadcasting options. For example, numpy.linalg.solve can handle “stacked” arrays, while scipy.linalg.solve accepts only a single square array as its first argument.
The term matrix as it is used on this page indicates a 2d numpy.array object, and not a numpy.matrix object. The latter is no longer recommended, even for linear algebra. See the matrix object documentation for more information.
The @ operator#
Introduced in NumPy 1.10.0, the @ operator is preferable to other methods when computing the matrix product between 2d arrays. The numpy.matmul function implements the @ operator.
Matrix and vector products#
Dot product of two arrays.
Compute the dot product of two or more arrays in a single function call, while automatically selecting the fastest evaluation order.
Return the dot product of two vectors.
Inner product of two arrays.
Compute the outer product of two vectors.
Matrix product of two arrays.
Compute tensor dot product along specified axes.
einsum (subscripts, *operands[, out, dtype, . ])
Evaluates the Einstein summation convention on the operands.
einsum_path (subscripts, *operands[, optimize])
Evaluates the lowest cost contraction order for an einsum expression by considering the creation of intermediate arrays.
Raise a square matrix to the (integer) power n.
Kronecker product of two arrays.
Decompositions#
Compute the qr factorization of a matrix.
linalg.svd (a[, full_matrices, compute_uv, . ])
Singular Value Decomposition.
Matrix eigenvalues#
Compute the eigenvalues and right eigenvectors of a square array.
Return the eigenvalues and eigenvectors of a complex Hermitian (conjugate symmetric) or a real symmetric matrix.
Compute the eigenvalues of a general matrix.
Compute the eigenvalues of a complex Hermitian or real symmetric matrix.
Norms and other numbers#
Compute the condition number of a matrix.
Compute the determinant of an array.
Return matrix rank of array using SVD method
Compute the sign and (natural) logarithm of the determinant of an array.
trace (a[, offset, axis1, axis2, dtype, out])
Return the sum along diagonals of the array.
Solving equations and inverting matrices#
Solve a linear matrix equation, or system of linear scalar equations.
Solve the tensor equation a x = b for x.
Return the least-squares solution to a linear matrix equation.
Compute the (multiplicative) inverse of a matrix.
Compute the (Moore-Penrose) pseudo-inverse of a matrix.
Compute the ‘inverse’ of an N-dimensional array.
Exceptions#
Generic Python-exception-derived object raised by linalg functions.
Linear algebra on several matrices at once#
Several of the linear algebra routines listed above are able to compute results for several matrices at once, if they are stacked into the same array.
This is indicated in the documentation via input parameter specifications such as a : (. M, M) array_like . This means that if for instance given an input array a.shape == (N, M, M) , it is interpreted as a “stack” of N matrices, each of size M-by-M. Similar specification applies to return values, for instance the determinant has det : (. ) and will in this case return an array of shape det(a).shape == (N,) . This generalizes to linear algebra operations on higher-dimensional arrays: the last 1 or 2 dimensions of a multidimensional array are interpreted as vectors or matrices, as appropriate for each operation.
Линейная алгебра на Python. [Урок 4]. Определитель матрицы
Четвертый урок из цикла “Линейная алгебра на Python“, посвящен понятию определителя матрицы и его свойствам.
Определитель матрицы
Определитель матрицы размера (n-го порядка) является одной из ее численных характеристик. Определитель матрицы A обозначается как |A| или det(A), его также называют детерминантом. Рассмотрим квадратную матрицу 2×2 в общем виде:
Определитель такой матрицы вычисляется следующим образом:
Перед тем, как привести методику расчета определителя в общем виде, введем понятие минора элемента определителя. Минор элемента определителя – это определитель, полученный из данного, путем вычеркивания всех элементов строки и столбца, на пересечении которых стоит данный элемент. Для матрицы 3×3 следующего вида:
Минор M23 будет выглядеть так:
Введем еще одно понятие – алгебраическое дополнение элемента определителя – это минор этого элемента, взятый со знаком плюс или минус :
В общем виде вычислить определитель матрицы можно через разложение определителя по элементам строки или столбца. Суть в том, что определитель равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения. Для матрицы 3×3 это правило будет выполняться следующим образом:
Это правило распространяется на матрицы любой размерности.
На Python определитель посчитать очень просто. Создадим матрицу A размера 3×3 из приведенного выше численного примера:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1') >>> print(A) [[-4 -1 2] [10 4 -1] [ 8 3 1]] Для вычисления определителя этой матрицы воспользуемся функцией det() из пакета linalg .
>>> np.linalg.det(A) -14.000000000000009
Мы уже говорили про особенность работы Python с числами с плавающей точкой, поэтому можете полученное значение округлить до -14 .
Свойства определителя матрицы.
Свойство 1 . Определитель матрицы остается неизменным при ее транспонировании:
Для округления чисел будем использовать функцию round() .
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1') >>> print(A) [[-4 -1 2] [10 4 -1] [ 8 3 1]] >>> print(A.T) [[-4 10 8] [-1 4 3] [ 2 -1 1]] >>> det_A = round(np.linalg.det(A), 3) >>> det_A_t = round(np.linalg.det(A.T), 3) >>> print(det_A) -14.0 >>> print(det_A_t) -14.0 Свойство 2 . Если у матрицы есть строка или столбец, состоящие из нулей, то определитель такой матрицы равен нулю:
>>> A = np.matrix('-4 -1 2; 0 0 0; 8 3 1') >>> print(A) [[-4 -1 2] [ 0 0 0] [ 8 3 1]] >>> np.linalg.det(A) 0.0 Свойство 3 . При перестановке строк матрицы знак ее определителя меняется на противоположный:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1') >>> print(A) [[-4 -1 2] [10 4 -1] [ 8 3 1]] >>> B = np.matrix('10 4 -1; -4 -1 2; 8 3 1') >>> print(B) [[10 4 -1] [-4 -1 2] [ 8 3 1]] >>> round(np.linalg.det(A), 3) -14.0 >>> round(np.linalg.det(B), 3) 14.0 Свойство 4 . Если у матрицы есть две одинаковые строки, то ее определитель равен нулю:
>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1') >>> print(A) [[-4 -1 2] [-4 -1 2] [ 8 3 1]] >>> np.linalg.det(A) 0.0 Свойство 5 . Если все элементы строки или столбца матрицы умножить на какое-то число, то и определитель будет умножен на это число:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1') >>> print(A) [[-4 -1 2] [10 4 -1] [ 8 3 1]] >>> k = 2 >>> B = A.copy() >>> B[2, :] = k * B[2, :] >>> print(B) [[-4 -1 2] [10 4 -1] [16 6 2]] >>> det_A = round(np.linalg.det(A), 3) >>> det_B = round(np.linalg.det(B), 3) >>> det_A * k -28.0 >>> det_B -28.0 Свойство 6 . Если все элементы строки или столбца можно представить как сумму двух слагаемых, то определитель такой матрицы равен сумме определителей двух соответствующих матриц:
>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1') >>> B = np.matrix('-4 -1 2; 8 3 2; 8 3 1') >>> C = A.copy() >>> C[1, :] += B[1, :] >>> print(C) [[-4 -1 2] [ 4 2 4] [ 8 3 1]] >>> print(A) [[-4 -1 2] [-4 -1 2] [ 8 3 1]] >>> print(B) [[-4 -1 2] [ 8 3 2] [ 8 3 1]] >>> round(np.linalg.det(C), 3) 4.0 >>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3) 4.0 Свойство 7 . Если к элементам одной строки прибавить элементы другой строки, умноженные на одно и тоже число, то определитель матрицы не изменится:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1') >>> k = 2 >>> B = A.copy() >>> B[1, :] = B[1, :] + k * B[0, :] >>> print(A) [[-4 -1 2] [10 4 -1] [ 8 3 1]] >>> print(B) [[-4 -1 2] [ 2 2 3] [ 8 3 1]] >>> round(np.linalg.det(A), 3) -14.0 >>> round(np.linalg.det(B), 3) -14.0 Свойство 8 . Если строка или столбец матрицы является линейной комбинацией других строк (столбцов), то определитель такой матрицы равен нулю:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1') >>> print(A) [[-4 -1 2] [10 4 -1] [ 8 3 1]] >>> k = 2 >>> A[1, :] = A[0, :] + k * A[2, :] >>> round(np.linalg.det(A), 3) 0.0 Свойство 9 . Если матрица содержит пропорциональные строки, то ее определитель равен нулю:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1') >>> print(A) [[-4 -1 2] [10 4 -1] [ 8 3 1]] >>> k = 2 >>> A[1, :] = k * A[0, :] >>> print(A) [[-4 -1 2] [-8 -2 4] [ 8 3 1]] >>> round(np.linalg.det(A), 3) 0.0 P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
NumPy, часть 4: linalg
В прошлых частях мы разбирались с основными операциями над массивами и randomом в NumPy. Теперь же мы приступим к более серьёзным вещам, которые есть в NumPy. Первый на очереди у нас модуль numpy.linalg, позволяющий делать многие операции из линейной алгебры.
Возведение в степень
linalg.matrix_power(M, n) — возводит матрицу в степень n.
Разложения
linalg.cholesky(a) — разложение Холецкого.
linalg.qr(a[, mode]) — QR разложение.
linalg.svd(a[, full_matrices, compute_uv]) — сингулярное разложение.
Некоторые характеристики матриц
linalg.eig(a) — собственные значения и собственные векторы.
linalg.norm(x[, ord, axis]) — норма вектора или оператора.
linalg.cond(x[, p]) — число обусловленности.
linalg.det(a) — определитель.
linalg.slogdet(a) — знак и логарифм определителя (для избежания переполнения, если сам определитель очень маленький).
Системы уравнений
linalg.solve(a, b) — решает систему линейных уравнений Ax = b.
linalg.tensorsolve(a, b[, axes]) — решает тензорную систему линейных уравнений Ax = b.
linalg.lstsq(a, b[, rcond]) — метод наименьших квадратов.
linalg.inv(a) — обратная матрица.
- linalg.LinAlgError — исключение, вызываемое данными функциями в случае неудачи (например, при попытке взять обратную матрицу от вырожденной).
- Подробная документация, как всегда, на английском: https://docs.scipy.org/doc/numpy/reference/routines.linalg.html
- Массивы большей размерности в большинстве функций linalg интерпретируются как набор из нескольких массивов нужной размерности. Таким образом, можно одним вызовом функции проделывать операции над несколькими объектами.
Для вставки кода на Python в комментарий заключайте его в теги
- Книги о Python
- GUI (графический интерфейс пользователя)
- Курсы Python
- Модули
- Новости мира Python
- NumPy
- Обработка данных
- Основы программирования
- Примеры программ
- Типы данных в Python
- Видео
- Python для Web
- Работа для Python-программистов