Наибольшая общая подстрока
Добрый день может кто-то знает как решить задачу? Заранее всем спасибо.
Даны K строк из маленьких латинских букв.
Требуется найти их наибольшую общую подстроку.
Входные данные
В первой строке число K (1 ≤ K ≤ 10). В следующих K строках — собственно K строк (длины строк от 1 до 10000).
Выходные данные
Наибольшая общая подстрока.
Пример
Входные данные:
3
abacaba
mycabarchive
acabistrue
Выходные данные:
cab
Проблема в том что время ограничено в 0,2с и память в 64мб.Так и еще слов может быть 10 и в каждом слове 10000 символов.
Училка подсказала что нужно использовать бинарный поиск + хеш + хеш-таблицы, чтобы ускорить алгоритм но чет не помогло((
Наибольшая общая подпоследовательность анаграммы
Даны две последовательности чисел, нужно найти самый длинный подотрезок в первой.
Выяснить, есть ли у двух строк общая подстрока длиной L
Условие Даны две строки s и t. Выясните, есть ли у них общая подстрока длиной L. Формат входных.
Наибольшая общая подпоследовательность
Общей подпоследовательностью двух строк s1 и s2 называется пара последовательностей индексов.
Наибольшая общая подстрока
Из ветки Рефал другого форума: Найти самую длинную подстроку двух строк, (f "ababab" "bababa") >.
Наибольшая общая подстрока
На днях отправил резюме в Яндекс. Откуда мне прислали задание-найти наибольшую общую подстроку.
Самая длинная общая подстрока Python
Задача состоит в том, чтобы найти самую длинную общую подстроку в заданной строке. Задача состоит в том, чтобы взять две строки и найти самую длинную общую подстроку с повторяющимися символами или без них. Другими словами, найти самую длинную общую подстроку, заданную в том же порядке и присутствующую в обеих строках. Например, «Tech» — это последовательность символов, заданная в «NextTech», которая также является подстрокой.
Процесс поиска самой длинной общей подпоследовательности:
Самый простой процесс поиска самой длинной общей подпоследовательности состоит в том, чтобы проверить каждый символ строки 1 и найти то же самое. последовательность в строке 2, проверяя каждый символ строки 2 один за другим, чтобы увидеть, является ли какая-либо подстрока общей в обеих строках. струны. Например, предположим, что у нас есть строка 1 «st1» и строка 2 «st2» с длинами a и b соответственно. Проверьте все подстроки «st1» и начните перебирать «st2», чтобы проверить, существует ли какая-либо подстрока «st1» как «st2». Начните с сопоставления подстроки длины 2 и увеличения длины на 1 на каждой итерации, доводя до максимальной длины строк.
Пример 1:
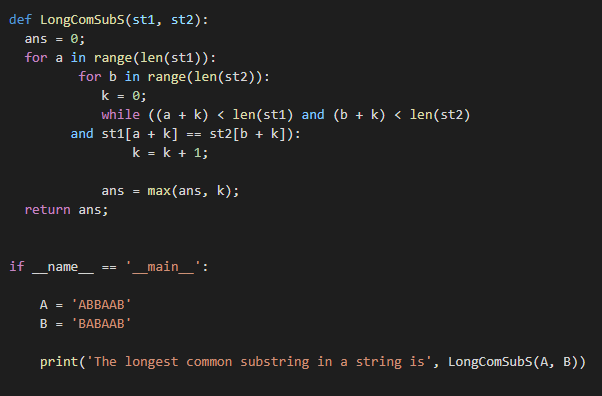
Этот пример посвящен поиску самой длинной общей подстроки с повторяющимися символами. Python предоставляет простые встроенные методы для выполнения любых функций. В приведенном ниже примере мы предоставили самый простой способ найти самую длинную общую подпоследовательность в двух строках. Комбинация циклов for и while используется для получения самой длинной общей подстроки в строке. Взгляните на пример, приведенный ниже:
деф LongComSubS ( ст1 , ст2 ) :
ответ = 0 ;
за а в диапазон ( Лен ( ст1 ) ) :
за б в диапазон ( Лен ( ст2 ) ) :
к = 0 ;
пока ( ( а + к ) < Лен ( ст1 ) и ( б + к ) < Лен ( ст2 )
и ст1 [ а + к ] == ст2 [ б + к ] ) :
к = к + 1 ;
ответ = Максимум ( ответ , к ) ;
возвращение ответ ;
если __название__ == ‘__главный__’ :
Распечатать ( ‘Самая длинная общая подстрока в строке’ , LongComSubS ( А , Б ) )
Следующий вывод будет получен после выполнения вышеуказанного кода. Он найдет самую длинную общую подстроку и выдаст вам результат.
Пример 2:
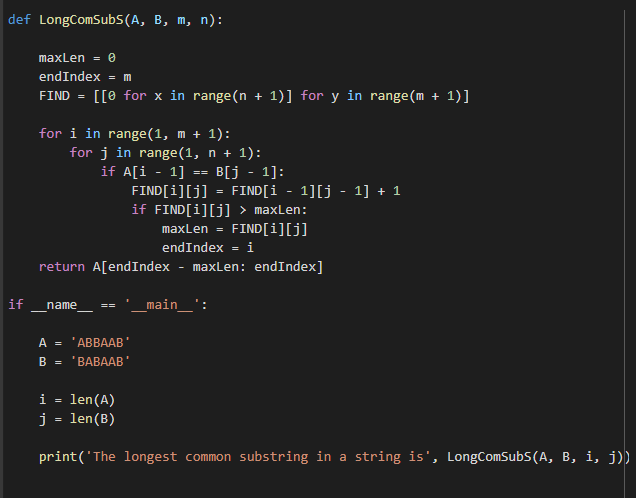
Другой способ найти самую длинную общую подстроку — использовать итеративный подход. Цикл for используется для итерации, а условие if соответствует общей подстроке.
деф LongComSubS ( А , Б , м , н ) :
НАЙТИ = [ [ 0 за Икс в диапазон ( п + 1 ) ] за у в диапазон ( м + 1 ) ]
за я в диапазон ( 1 , м + 1 ) :
за Дж в диапазон ( 1 , п + 1 ) :
если А [ я — 1 ] == Б [ дж — 1 ] :
НАЙТИ [ я ] [ Дж ] = НАЙТИ [ я — 1 ] [ дж — 1 ] + 1
если НАЙТИ [ я ] [ Дж ] > максДлен:
макслен = НАЙТИ [ я ] [ Дж ]
endIndex = я
возвращение Икс [ endIndex — maxLen: endIndex ]
если __название__ == ‘__главный__’ :
Распечатать ( ‘Самая длинная общая подстрока в строке’ , LongComSubS ( А , Б , я , Дж ) )
Выполните приведенный выше код в любом интерпретаторе Python, чтобы получить желаемый результат. Однако мы использовали инструмент Spyder для выполнения программы поиска самой длинной общей подстроки в строке. Вот вывод приведенного выше кода:
Пример 3:
Вот еще один пример, который поможет вам найти самую длинную общую подстроку в строке, используя кодирование Python. Этот метод является самым маленьким, простым и легким способом найти самую длинную общую подпоследовательность. Взгляните на пример кода, приведенный ниже:
деф _итер ( ) :
за а , б в молния ( ст1 , ст2 ) :
если а == б:
урожай а
еще :
возвращение
возвращение » . присоединиться ( _итер ( ) )
если __название__ == ‘__главный__’ :
Распечатать ( ‘Самая длинная общая подстрока в строке’ , LongComSubS ( А , Б ) )
Ниже вы можете найти вывод кода, приведенного выше.
Используя этот метод, мы вернули не общую подстроку, а длину этой общей подстроки. Чтобы помочь вам получить желаемый результат, мы показали как результаты, так и методы получения этих результатов.
Временная сложность и пространственная сложность для нахождения самой длинной общей подстроки
За выполнение или выполнение любой функции нужно платить; временная сложность является одной из этих затрат. Временная сложность любой функции рассчитывается путем анализа того, сколько времени может потребоваться для выполнения оператора. Следовательно, чтобы найти все подстроки в «st1», нам нужно O (a ^ 2), где «a» — длина «st1», а «O» — символ временной сложности. Однако временная сложность итерации и определение того, существует ли подстрока в «st2» или нет, составляет O (m), где «m» — длина «st2». Таким образом, общая временная сложность обнаружения самой длинной общей подстроки в двух строках составляет O(a^2*m). Более того, объемная сложность — это еще одна стоимость выполнения программы. Сложность пространства представляет собой пространство, которое программа или функция будет сохранять в памяти во время выполнения. Следовательно, пространственная сложность поиска самой длинной общей подпоследовательности составляет O (1), поскольку для ее выполнения не требуется никакого места.
Вывод:
В этой статье мы узнали о методах поиска самой длинной общей подстроки в строке с помощью программирования на Python. Мы предоставили три простых и легких примера, чтобы получить самую длинную общую подстроку в python. В первом примере используется комбинация циклов for и while. В то время как во втором примере мы следовали итеративному подходу, используя цикл for и логику if. Напротив, в третьем примере мы просто использовали встроенную функцию python для получения длины общей подстроки в строке. Напротив, временная сложность поиска самой длинной общей подстроки в строке с использованием python составляет O (a ^ 2 * m), где a и ma — длина двух строк; строка 1 и строка 2 соответственно.
Проблема с самой длинной общей подстрокой
Самая длинная общая проблема подстроки — это проблема поиска самой длинной строки (или строк), которая является подстрокой (или подстроками) двух строк.
Задача отличается от задачи поиска Самая длинная общая подпоследовательность (LCS). В отличие от подпоследовательностей, подстроки должны занимать последовательные позиции в исходной строке.
Например, самая длинная общая подстрока строк ABABC , BABCA это строка BABC длина 4. Другие распространенные подстроки: ABC , A , AB , B , BA , BC , а также C .
Наивным решением было бы рассмотреть все подстроки второй строки и найти самую длинную подстроку, которая также является подстрокой первой строки. Временная сложность этого решения будет O((m + n) × m 2 ) , куда m а также n длина строк X а также Y , сколько потребуется (m+n) время для поиска подстроки, и есть m 2 подстроки второй строки. Мы можем оптимизировать этот метод, рассматривая подстроки в порядке уменьшения их длины и возвращая значение, как только любая подстрока совпадает с первой строкой. Но временная сложность в наихудшем случае остается неизменной, когда отсутствуют общие символы.
Можем ли мы сделать лучше?
Идея состоит в том, чтобы найти самый длинный общий суффикс для всех пар префиксов строк с помощью динамического программирования, используя отношение:
LCSuffix[i][j] = | LCSuffix[i-1][j-1] + 1 (if X[i-1] = Y[j-1])
| 0 (otherwise)
Например, рассмотрим строки ABAB а также BABA .
Наконец, самая длинная общая длина подстроки будет максимальной из этих самых длинных общих суффиксов всех возможных префиксов.
Следующее решение на C++, Java и Python находит длину самой длинной повторяющейся подпоследовательности последовательностей. X а также Y итеративно с использованием оптимальное основание собственность проблема ЛКС.