Плотность вероятности нормального распределения python

Python для анализа данных¶

Нам пригодится только модуль scipy.stats . Полное описание доступно по ссылке. По ссылке можно прочитать полную документацию по работе с непрерывными (Continuous), дискретными (Discrete) и многомерными (Multivariate) распределениями. Пакет также предоставляет некоторое количество статистических методов, которые рассматриваются в курсах статистики.

import scipy.stats as sps import numpy as np import ipywidgets as widgets import matplotlib.pyplot as plt %matplotlib inline

1. Работа с библиотекой scipy.stats .¶

• X(params).rvs(size=N) — генерация выборки размера $N$ (Random VariateS). Возвращает numpy.array ;
• X(params).cdf(x) — значение функции распределения в точке $x$ (Cumulative Distribution Function);
• X(params).logcdf(x) — значение логарифма функции распределения в точке $x$;
• X(params).ppf(q) — $q$-квантиль (Percent Point Function);
• X(params).mean() — математическое ожидание;
• X(params).median() — медиана ($1/2$-квантиль);
• X(params).var() — дисперсия (Variance);
• X(params).std() — стандартное отклонение = корень из дисперсии (Standard Deviation).

Кроме того для непрерывных распределений определены функции

• X(params).pdf(x) — значение плотности в точке $x$ (Probability Density Function);
• X(params).logpdf(x) — значение логарифма плотности в точке $x$.

• X(params).pmf(k) — значение дискретной плотности в точке $k$ (Probability Mass Function);
• X(params).logpdf(k) — значение логарифма дискретной плотности в точке $k$.

Все перечисленные выше методы применимы как к конкретному распределению X(params) , так и к самому классу X . Во втором случае параметры передаются в сам метод. Например, вызов X.rvs(size=N, params) эквивалентен X(params).rvs(size=N) . При работе с распределениями и случайными величинами рекомендуем использовать первый способ, посколько он больше согласуется с математическим синтаксисом теории вероятностей.

Параметры могут быть следующими:

• loc — параметр сдвига;
• scale — параметр масштаба;
• и другие параметры (например, $n$ и $p$ для биномиального).

Для примера сгенерируем выборку размера $N = 200$ из распределения $\mathcal(1, 9)$ и посчитаем некоторые статистики. В терминах выше описанных функций у нас $X$ = sps.norm , а params = ( loc=1, scale=3 ).

Примечание. Выборка — набор независимых одинаково распределенных случайных величин. Часто в разговорной речи выборку отождествляют с ее реализацией — значения случайных величин из выборки при «выпавшем» элементарном исходе.

sample = sps.norm(loc=1, scale=3).rvs(size=200) print('Первые 10 значений выборки:\n', sample[:10]) print('Выборочное среденее: %.3f' % sample.mean()) print('Выборочная дисперсия: %.3f' % sample.var()) 

Первые 10 значений выборки: [ 0.65179639 -0.66437884 0.61450407 -0.1828078 0.42271419 0.14424901 2.01547486 7.81094724 -1.35246891 -1.35574313] Выборочное среденее: 0.854 Выборочная дисперсия: 9.118

Источник

scipy.stats.norm#

The location ( loc ) keyword specifies the mean. The scale ( scale ) keyword specifies the standard deviation.

As an instance of the rv_continuous class, norm object inherits from it a collection of generic methods (see below for the full list), and completes them with details specific for this particular distribution.

The probability density function for norm is:

The probability density above is defined in the “standardized” form. To shift and/or scale the distribution use the loc and scale parameters. Specifically, norm.pdf(x, loc, scale) is identically equivalent to norm.pdf(y) / scale with y = (x — loc) / scale . Note that shifting the location of a distribution does not make it a “noncentral” distribution; noncentral generalizations of some distributions are available in separate classes.

>>> import numpy as np >>> from scipy.stats import norm >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1) 

Calculate the first four moments:

>>> mean, var, skew, kurt = norm.stats(moments='mvsk') 

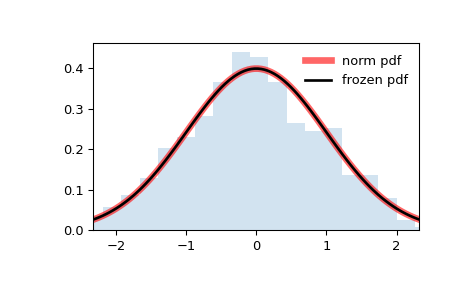
Display the probability density function ( pdf ):

>>> x = np.linspace(norm.ppf(0.01), . norm.ppf(0.99), 100) >>> ax.plot(x, norm.pdf(x), . 'r-', lw=5, alpha=0.6, label='norm pdf') 

Alternatively, the distribution object can be called (as a function) to fix the shape, location and scale parameters. This returns a “frozen” RV object holding the given parameters fixed.

Freeze the distribution and display the frozen pdf :

>>> rv = norm() >>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf') 

Check accuracy of cdf and ppf :

>>> vals = norm.ppf([0.001, 0.5, 0.999]) >>> np.allclose([0.001, 0.5, 0.999], norm.cdf(vals)) True 

And compare the histogram:

>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2) >>> ax.set_xlim([x[0], x[-1]]) >>> ax.legend(loc='best', frameon=False) >>> plt.show() 

rvs(loc=0, scale=1, size=1, random_state=None)

pdf(x, loc=0, scale=1)

Probability density function.

logpdf(x, loc=0, scale=1)

Log of the probability density function.

cdf(x, loc=0, scale=1)

Cumulative distribution function.

logcdf(x, loc=0, scale=1)

Log of the cumulative distribution function.

sf(x, loc=0, scale=1)

Survival function (also defined as 1 — cdf , but sf is sometimes more accurate).

logsf(x, loc=0, scale=1)

Log of the survival function.

ppf(q, loc=0, scale=1)

Percent point function (inverse of cdf — percentiles).

isf(q, loc=0, scale=1)

Inverse survival function (inverse of sf ).

moment(order, loc=0, scale=1)

Non-central moment of the specified order.

stats(loc=0, scale=1, moments=’mv’)

Mean(‘m’), variance(‘v’), skew(‘s’), and/or kurtosis(‘k’).

entropy(loc=0, scale=1)

(Differential) entropy of the RV.

Parameter estimates for generic data. See scipy.stats.rv_continuous.fit for detailed documentation of the keyword arguments.

expect(func, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)

Expected value of a function (of one argument) with respect to the distribution.

median(loc=0, scale=1)

Median of the distribution.

mean(loc=0, scale=1)

var(loc=0, scale=1)

Variance of the distribution.

std(loc=0, scale=1)

Standard deviation of the distribution.

interval(confidence, loc=0, scale=1)

Confidence interval with equal areas around the median.

Источник

Модуль random. Часть 3

Рассмотрим равномерное и нормальное распределения непрерывной случайной величины.

• Непрерывное вероятностное распределение
  • Непрерывное равноемерное распределение
    • Плотность вероятности
    • Матожидание и дисперсия
    • Реализация на Питоне
    • Разница между np.random.random(), np.random.rand() и np.random.uniform()
    • Функция плотности нормального распределения
    • Функция np.random.normal()
    • Расчет вероятности
    • Функция плотности и функция распределения
    • Вероятность конкретного значения
    • Формирование выборки
    • Центральная предельная теорема
      • Определения и нотация
      • ЦПТ и нормальное распределение
      • Проверим на Питоне
      • Способ 1. График нормальной вероятности
      • Способ 2. Тест Шапиро-Уилка
      • Поправка на непрерывность распределения
      • Пример приближения

      Непрерывное вероятностное распределение

      Как уже было сказано, в отличие от дискретной величины, непрерывная величина может принимать любое значение в заданном интервале.

      Непрерывное равноемерное распределение

      Непрерывное равномерное распределение (continuous uniform distribution) описывает случайную величину, вероятность значений которой одинакова на заданном интервале от a до b.

      Например, если мы знаем, что автобус приходит на остановку каждые 12 минут, то время ожидания автобуса на остановке равномерно распределено между 0 и 12 минутами.

      Плотность вероятности

      Непрерывное распределение (в отличие от дискретного) задается плотностью вероятности (probability density function, pdf). Для равномерного непрерывного распределения плотность вероятности задается вот такой несложной функцией.

      $$ pdf(x) = \begin \frac, x \in [a, b] \ 0, x \notin [a, b] \end $$

      В примере с ожиданием автобуса вероятность его приезда в любой момент в пределах заданного интервала равна

      $$ pdf(x) = \begin \frac = \frac, x \in [0, 12] \ 0, x \notin [0, 12] \end $$

      На графике равномерное распределение представляет собой прямоугольник, площадь которого всегда равна единице.

      

      Если мы хотим посчитать вероятность приезда автобуса в пределах заданного интервала ожидания, нам, по сути, нужно рассчитать отдельный участок площади прямоугольника.

      Например, вероятность приезда автобуса при ожидании до 12 минут включительно составляет 1.00 или 100%, потому что такой промежуток включает всю площадь прямоугольника.

      Теперь давайте рассчитаем вероятность ожидания автобуса до 7 минут включительно. Нас будет интересовать интервал от 0 до 7 минут и соответствующий участок площади прямоугольника.

      

      Применив несложную формулу, мы без труда вычислим площадь этого участка.

      $$ P(7) = \frac \times 7 \approx 0,583 $$

      Матожидание и дисперсия

      Остается рассчитать матожидание (среднее время ожидания автобуса) и дисперсию.

      Реализация на Питоне

      Воспользуемся функцией np.random.uniform() для того, чтобы создать равномерное распределение с параметрами U(0, 12).

      Источник

      Как построить нормальное распределение в Python (с примерами)

      

      Чтобы построить нормальное распределение в Python, вы можете использовать следующий синтаксис:

      #x-axis ranges from -3 and 3 with .001 steps x = np.arange (-3, 3, 0.001) #plot normal distribution with mean 0 and standard deviation 1 plt.plot (x, norm. pdf (x, 0, 1)) 

      Массив x определяет диапазон для оси x, а plt.plot() создает кривую для нормального распределения с указанным средним значением и стандартным отклонением.

      В следующих примерах показано, как использовать эти функции на практике.

      Пример 1: построение одного нормального распределения

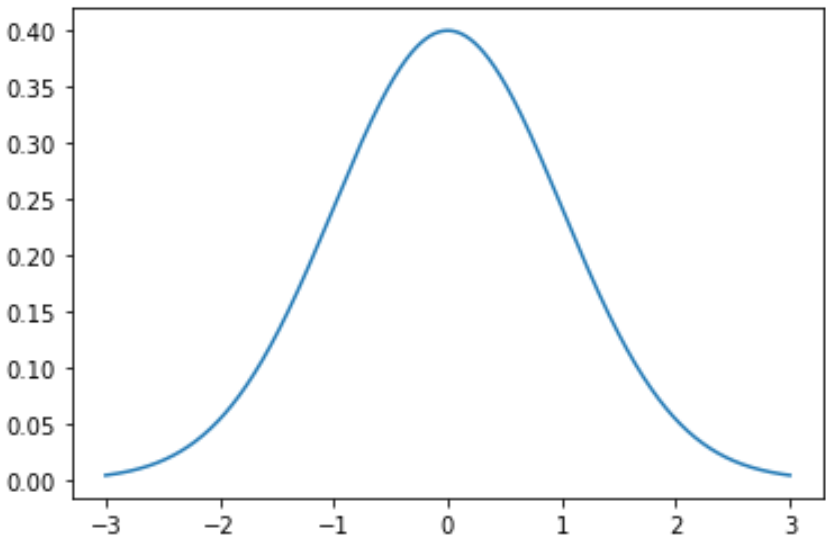
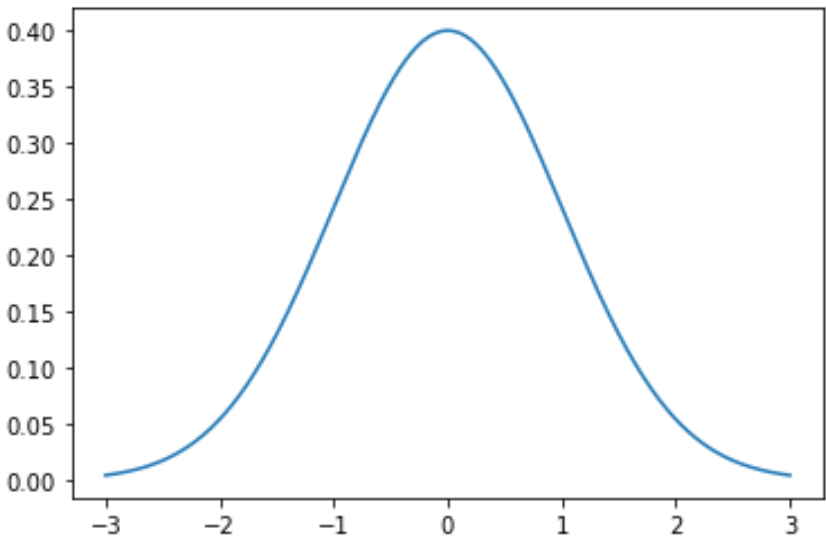
      Следующий код показывает, как построить одну кривую нормального распределения со средним значением 0 и стандартным отклонением 1:

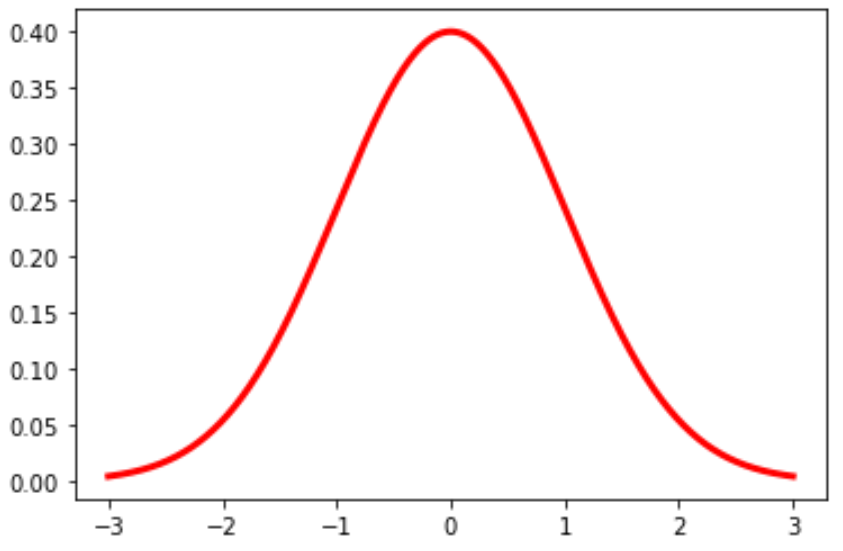
      import numpy as np import matplotlib.pyplot as plt from scipy. stats import norm #x-axis ranges from -3 and 3 with .001 steps x = np.arange (-3, 3, 0.001) #plot normal distribution with mean 0 and standard deviation 1 plt.plot (x, norm. pdf (x, 0, 1)) 

      

      Вы также можете изменить цвет и ширину линии на графике:

      plt.plot (x, norm. pdf (x, 0, 1), color='red', linewidth= 3 ) 

      

      Пример 2: построение нескольких нормальных распределений

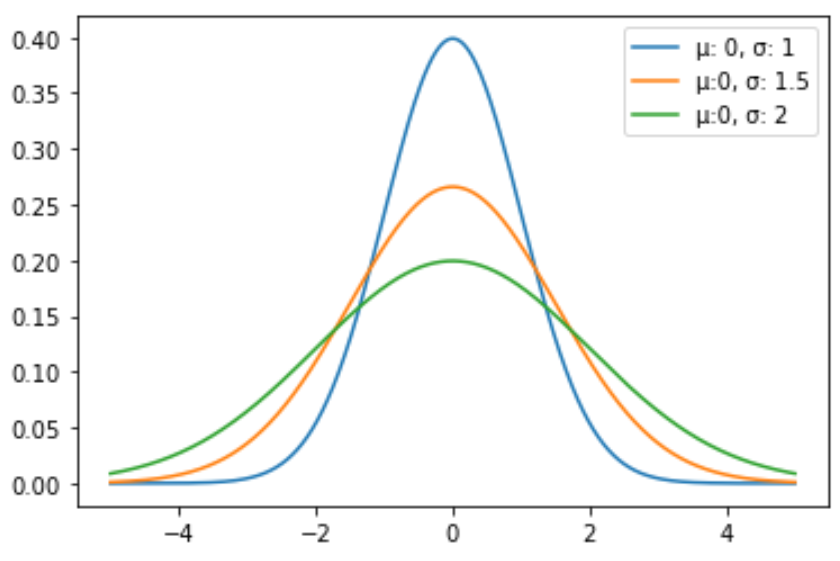
      Следующий код показывает, как построить несколько кривых нормального распределения с разными средними значениями и стандартными отклонениями:

      import numpy as np import matplotlib.pyplot as plt from scipy. stats import norm #x-axis ranges from -5 and 5 with .001 steps x = np.arange (-5, 5, 0.001) #define multiple normal distributions plt.plot (x, norm. pdf (x, 0, 1), label='μ: 0, σ: 1') plt.plot (x, norm. pdf (x, 0, 1.5), label='μ:0, σ: 1.5') plt.plot (x, norm. pdf (x, 0, 2), label='μ:0, σ: 2') #add legend to plot plt.legend() 

      

      Не стесняйтесь изменять цвета линий и добавлять заголовок и метки осей, чтобы сделать диаграмму завершенной:

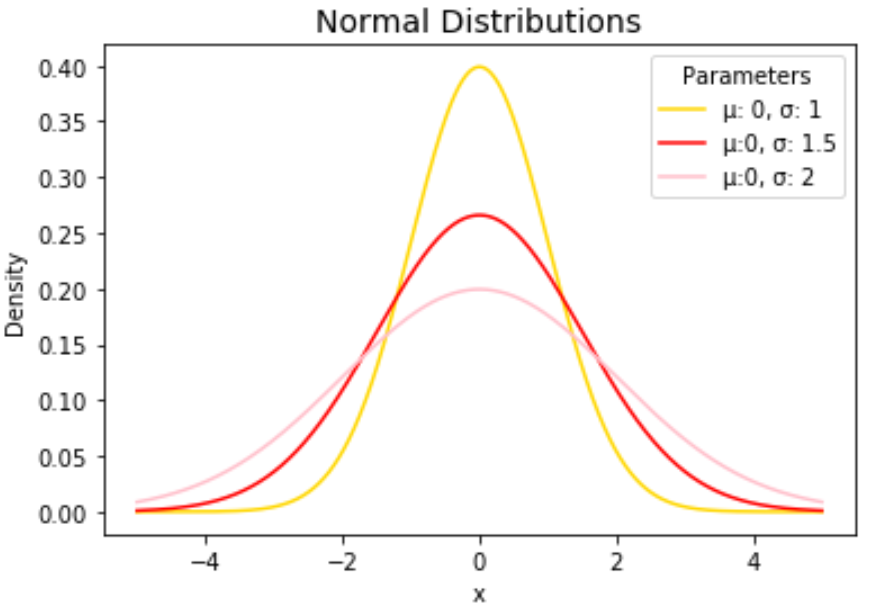
      import numpy as np import matplotlib.pyplot as plt from scipy. stats import norm #x-axis ranges from -5 and 5 with .001 steps x = np.arange (-5, 5, 0.001) #define multiple normal distributions plt.plot (x, norm. pdf (x, 0, 1), label='μ: 0, σ: 1', color='gold') plt.plot (x, norm. pdf (x, 0, 1.5), label='μ:0, σ: 1.5', color='red') plt.plot (x, norm. pdf (x, 0, 2), label='μ:0, σ: 2', color='pink') #add legend to plot plt.legend(title='Parameters') #add axes labels and a title plt.ylabel('Density') plt.xlabel('x') plt.title('Normal Distributions', fontsize= 14 ) 

      

      Подробное описание функции plt.plot() см. в документации по matplotlib.

      Источник