Питон сумма ряда чисел

Сумма ряда натуральных чисел на Питоне

Попробуем на практике разобрать работу циклов, про которые рассказано в одном из наших уроков. Выполним предложенное задание, использовав несколько разных методик и видов циклов.

Задача

Решение задачи с помощью цикла while

Произведём расчёт, используя цикл с предусловием while.

n=int(input(Введите последнее число из ряда натуральных чисел=)) 
i=1 
s=0 
while i s=i+s 
i=i+1 
print (Сумма чисел от 1 до, n, =, s)

1. Сперва задаем в переменную n самое большое натуральное число (в пределах разумного).
2. Обнулим на входе сумму s.
3. Цикл будет выполняться до тех пор, пока внутренняя переменная не достигнет значения n.

Результат выполнения программы

Решение задачи с помощью цикла for

Быстрее происходит расчёт при помощи цикла for.

n=int(input(Введите последнее число=)) 
s=0 
for i in range(1,n+1): 
s=i+s 
print (Сумма чисел от 1 до, n, =, s)

Посмотрите, в цикле записано максимальное число не n, а n+1. Это связано с тем, что цикл должен выполняться на один шаг больше, чтобы последнее значение промежуточной суммы было учтено.

Результат выполнения программы

Решение задачи с помощью списка

Ту же самую задачку можно решить, используя список. По сути, это ничего не меняет, но, как видите, код при этом занимает всего две строки:

n=int(input(Введите последнее число=)) 
print (Сумма чисел от 1 до, n, =, sum([i for i in range(1,n+1)]))

Результат выполнения программы

Источник

Питон сумма ряда чисел

Last updated: Feb 19, 2023
Reading time · 4 min

# Table of Contents

# Sum all numbers in a range in Python

To sum all numbers in a range:

1. Use the range() class to get a range of numbers.
2. Pass the range object to the sum() function.
3. The sum() function will return the sum of the integers in the range.

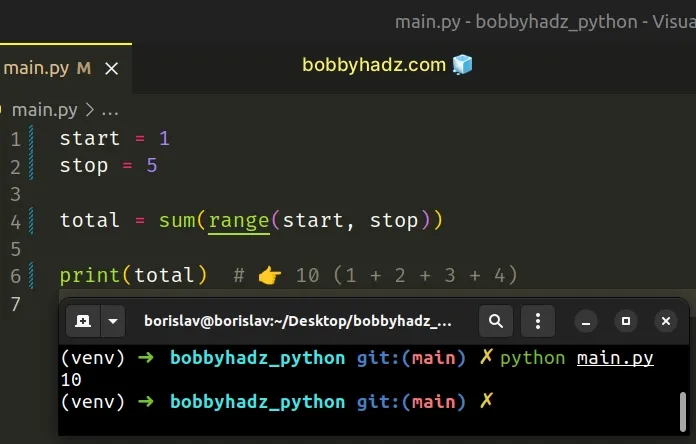
Copied! 
start = 1 stop = 5 total = sum(range(start, stop)) print(total) # 👉️ 10 (1 + 2 + 3 + 4) 

We used the range() class to get a range of numbers.

The range class is commonly used for looping a specific number of times in for loops and takes the following arguments:

Name	Description
start	An integer representing the start of the range (defaults to 0 )
stop	Go up to, but not including the provided integer
step	Range will consist of every N numbers from start to stop (defaults to 1 )

If you only pass a single argument to the range() constructor, it is considered to be the value for the stop parameter.

Copied! 
# 👇️ [0, 1, 2, 3, 4] print(list(range(5))) total = sum(range(5)) print(total) # 👉️ 10 

The example shows that if the start argument is omitted, it defaults to 0 and if the step argument is omitted, it defaults to 1 .

If values for the start and stop parameters are provided, the start value is inclusive, whereas the stop value is exclusive.

Copied! 
# 👇️ [1, 2, 3, 4] print(list(range(1, 5))) total = sum(range(1, 5)) print(total) # 👉️ 10 

If the value for the stop parameter is lower than the value for the start parameter, the range will be empty.

Copied! 
# 👇️ [] print(list(range(5, 1))) total = sum(range(5, 1)) print(total) # 👉️ 0 

The sum function can be used to calculate the sum of the numbers in the range.

The sum function takes an iterable, sums its items from left to right and returns the total.

The sum function takes the following 2 arguments:

Name	Description
iterable	the iterable whose items to sum
start	sums the start value and the items of the iterable. sum defaults to 0 (optional)

# Sum the numbers in a range with a step in Python

If you need to get a range with a step, pass a value for the third argument of the range() class.

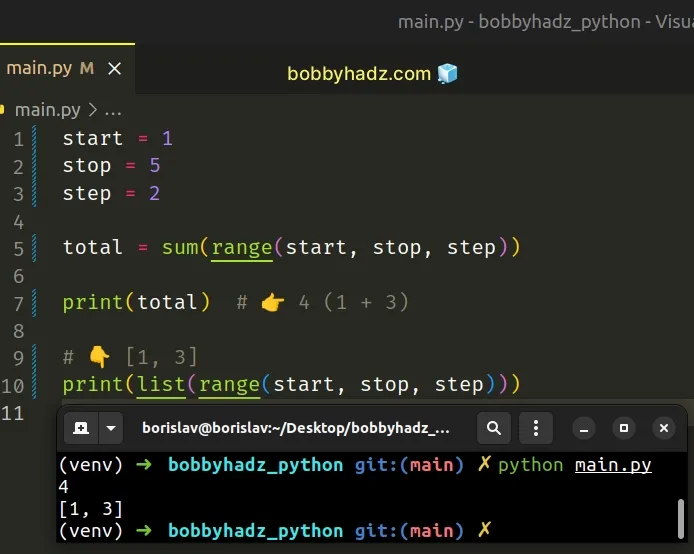
Copied! 
start = 1 stop = 5 step = 2 total = sum(range(start, stop, step)) print(total) # 👉️ 4 (1 + 3) # 👇️ [1, 3] print(list(range(start, stop, step))) 

When the step argument is provided, the range will consist of every N numbers from start to stop .

The value for the step argument defaults to 1 .

# Creating a reusable function

If you have to do this often, define a reusable function.

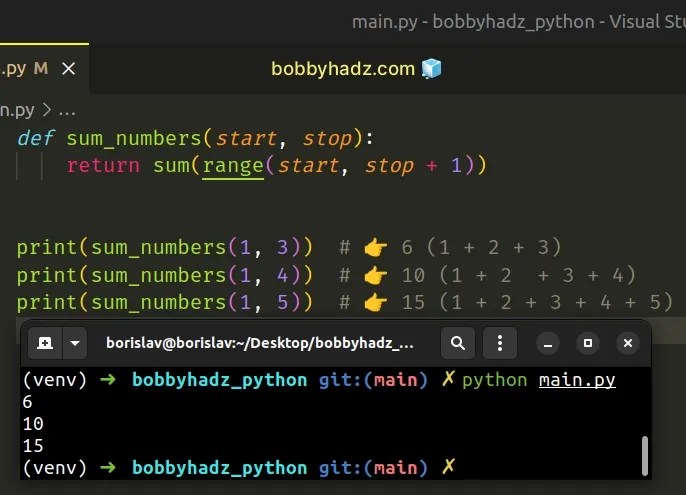
Copied! 
def sum_numbers(start, stop): return sum(range(start, stop + 1)) print(sum_numbers(1, 3)) # 👉️ 6 (1 + 2 + 3) print(sum_numbers(1, 4)) # 👉️ 10 (1 + 2 + 3 + 4) print(sum_numbers(1, 5)) # 👉️ 15 (1 + 2 + 3 + 4 + 5) 

The function takes start and stop values and sums the numbers from start to stop .

Notice that we added 1 to the stop value to make the range inclusive.

If you want to exclude the last number from the range, remove the addition operator.

Copied! 
def sum_numbers(start, stop): return sum(range(start, stop)) print(sum_numbers(1, 3)) # 👉️ 3 (1 + 2) print(sum_numbers(1, 4)) # 👉️ 6 (1 + 2 + 3) print(sum_numbers(1, 5)) # 👉️ 10 (1 + 2 + 3 + 4) 

# Sum the Integers from 1 to N in Python

Multiply by n + 1 and floor-divide by 2 to get the integers from 1 to N.

The result will be the sum of the integers from 1 to N (including N).

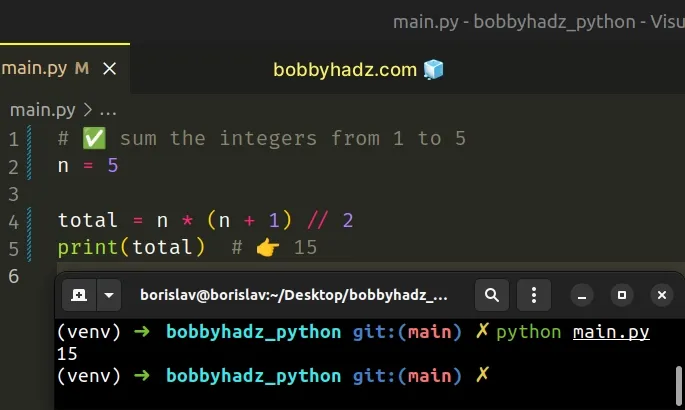
Copied! 
# ✅ sum the integers from 1 to 5 n = 5 total = n * (n + 1) // 2 print(total) # 👉️ 15 

The example multiplies n by n + 1 and floor-divides by 2 to get the sum of the integers from 1 to n .

The result of using the floor division operator is that of a mathematical division with the floor() function applied to the result.

Here is an example that sums the integers from 1 to 100.

Copied! 
n = 100 total = n * (n + 1) // 2 print(total) # 👉️ 5050 

All we had to do is update the value of n to get the sum of the integers from 1 to 100 .

If you don’t want to use a formula, use the range() class from the previous subheading.

# Sum the numbers in a range that are divisible by N

If you need to sum the numbers in a range that are divisible by N, use a while loop.

Copied! 
def sum_divisible_in_range(start, stop, divisor): while start % divisor != 0: start += 1 return sum(range(start, stop, divisor)) print(sum_divisible_in_range(1, 6, 2)) # 👉️ 6 print(sum_divisible_in_range(1, 7, 3)) # 👉️ 9 print(sum_divisible_in_range(1, 8, 4)) # 👉️ 4 

we used a while loop to iterate until the start value reaches the divisor .

The last step is to create a range with the start , stop and divisor values and sum them.

# Additional Resources

You can learn more about the related topics by checking out the following tutorials:

I wrote a book in which I share everything I know about how to become a better, more efficient programmer.

Источник

Сумма ряда 1 / n^2

Сумма ряда/Вычислить приближенное значение элементарных функций как сумму ряда
Для начала, здравствуйте. У меня возникла проблема в понимании смысла задачи. А задача вот: .

Найти номер члена ряда, начиная с которого сумма ряда будет больше заданного А
Всем привет! Мы еще даже не изучали эту тему с "Суммой ряда", а просят найти Переработать.

Сумма ряда с точностью до члена ряда
Найти сумму ряда с точностью до члена ряда, меньшего ε(задается с клавиатуры) для заданного.

n=int(input()) seqSum=0.0 i=1 while in: s=1.0/(i**2) seqSum +=s i=i+1 print(s)

n=int(input()) print(sum([1/(i**2) for i in range(1, n+1)]))

Сообщение от oldnewyear

Сообщение от palva

n=int(input()) seqSum=0.0 i=1 while in: s=1.0/(i**2) seqSum +=s i=i+1 print(s)

n=int(input()) seqSum=0.0 i=1 while in: s=1.0/(i**2) seqSum +=s i=i+1 print(seqSum)

Сообщение от oldnewyear

вот этот код дает правильный ответ, а ваш при n=3
0.25

n=int(input())
print(sum([1/(i**2) for i in range(1, n+1)]))
ответ при n=3 1.36111
т.к с оператором for не разобрался толком. исправьте с while. я же хочу научиться, а не просто ответ впихнуть. хочу понять свою ошибку

Добавлено через 15 минут
спасибо!
получается у меня был правильный код, на 87,5%, и я ходил вокруг да около. я ведь до того как сюда написать, долго пробовал.

n=int(input()) i=2 s=1 while i != n + 1: s += 1/(i**2) i += 1 print(s)

n = int(input()) a = 1 sPrev = (1 / a ** 2) sNext = sPrev i = 1 while i != n: i += 1 a += 1 sNext = sPrev + (1 / a ** 2) sPrev = sNext print('%.5f' % sNext)

Источник