Пирамидальная сортировка java код

Heap Sort – Data Structures and Algorithms Tutorials

Heap sort is a comparison-based sorting technique based on Binary Heap data structure. It is similar to the selection sort where we first find the minimum element and place the minimum element at the beginning. Repeat the same process for the remaining elements.

Heap Sort Algorithm

To solve the problem follow the below idea:

• Build a heap from the given input array.
• Repeat the following steps until the heap contains only one element:
  • Swap the root element of the heap (which is the largest element) with the last element of the heap.
  • Remove the last element of the heap (which is now in the correct position).
  • Heapify the remaining elements of the heap.

  Detailed Working of Heap Sort

  To understand heap sort more clearly, let’s take an unsorted array and try to sort it using heap sort.
  Consider the array: arr[] = .

  Build Complete Binary Tree: Build a complete binary tree from the array.

  

  Heap sort algorithm | Build Complete Binary Tree

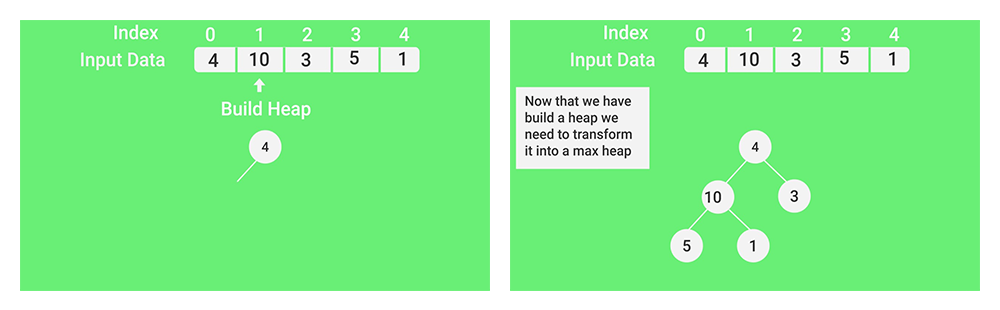
  • To transform a heap into a max-heap, the parent node should always be greater than or equal to the child nodes
    • Here, in this example, as the parent node 4 is smaller than the child node 10, thus, swap them to build a max-heap.

    

    Heap sort algorithm | Max Heapify constructed binary tree

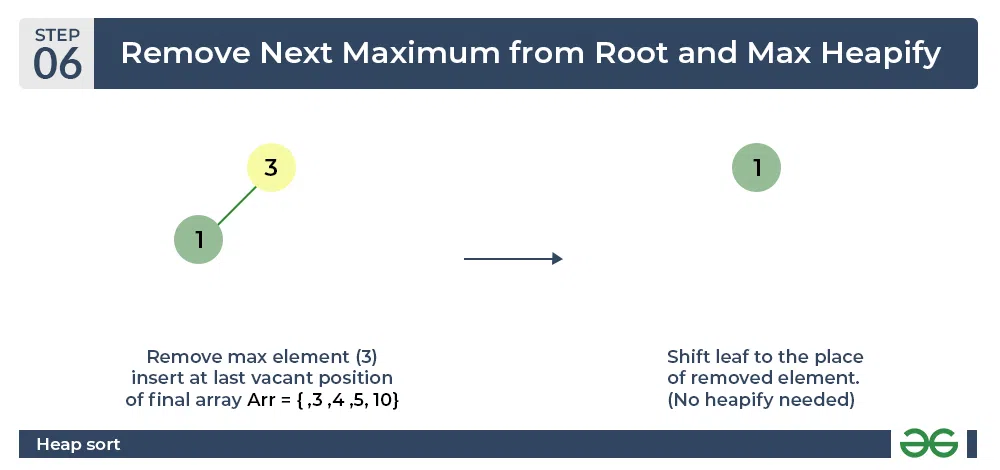
    Perform heap sort: Remove the maximum element in each step (i.e., move it to the end position and remove that) and then consider the remaining elements and transform it into a max heap.

    • Delete the root element (10) from the max heap. In order to delete this node, try to swap it with the last node, i.e. (1). After removing the root element, again heapify it to convert it into max heap.
      • Resulted heap and array should look like this:

      

      Heap sort algorithm | Remove maximum from root and max heapify

      

      Heap sort algorithm | Remove next maximum from root nad max heapify

      

      Heap sort algorithm | Repeat previous step

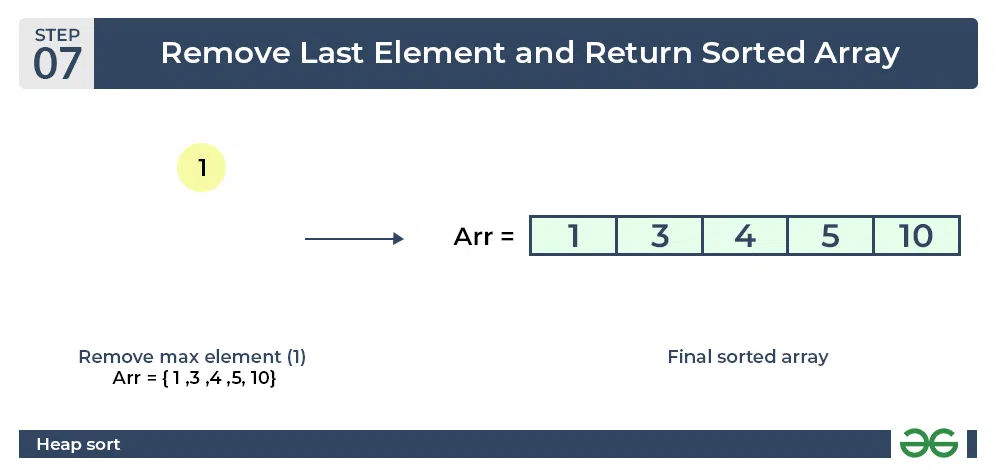
      • Now when the root is removed once again it is sorted. and the sorted array will be like arr[] = .

      

      Heap sort algorithm | Final sorted array

      Источник

      Пирамидальная сортировка (HeapSort)

      

      Пирамидальная сортировка (или сортировка кучей, HeapSort) — это метод сортировки сравнением, основанный на такой структуре данных как двоичная куча. Она похожа на сортировку выбором, где мы сначала ищем максимальный элемент и помещаем его в конец. Далее мы повторяем ту же операцию для оставшихся элементов.

      Что такое двоичная куча?

      Давайте сначала определим законченное двоичное дерево. Законченное двоичное дерево — это двоичное дерево, в котором каждый уровень, за исключением, возможно, последнего, имеет полный набор узлов, и все листья расположены как можно левее (Источник Википедия).

      Двоичная куча — это законченное двоичное дерево, в котором элементы хранятся в особом порядке: значение в родительском узле больше (или меньше) значений в его двух дочерних узлах. Первый вариант называется max-heap, а второй — min-heap. Куча может быть представлена двоичным деревом или массивом.

      Почему для двоичной кучи используется представление на основе массива ?

      Поскольку двоичная куча — это законченное двоичное дерево, ее можно легко представить в виде массива, а представление на основе массива является эффективным с точки зрения расхода памяти. Если родительский узел хранится в индексе I, левый дочерний элемент может быть вычислен как 2 I + 1, а правый дочерний элемент — как 2 I + 2 (при условии, что индексирование начинается с 0).

      Алгоритм пирамидальной сортировки в порядке по возрастанию:

      1. Постройте max-heap из входных данных.
      2. На данном этапе самый большой элемент хранится в корне кучи. Замените его на последний элемент кучи, а затем уменьшите ее размер на 1. Наконец, преобразуйте полученное дерево в max-heap с новым корнем.
      3. Повторяйте вышеуказанные шаги, пока размер кучи больше 1.

      Как построить кучу?

      Процедура преобразования в кучу (далее процедура heapify) может быть применена к узлу, только если его дочерние узлы уже преобразованы. Таким образом, преобразование должно выполняться снизу вверх. Давайте разберемся с помощью примера:

      Входные данные: 4, 10, 3, 5, 1 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) Числа в скобках представляют индексы в представлении данных в виде массива. Применение процедуры heapify к индексу 1: 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) Применение процедуры heapify к индексу 0: 10(0) / \ 5(1) 3(2) / \ 4(3) 1(4) Процедура heapify вызывает себя рекурсивно для создания кучи сверху вниз.

      // Реализация пирамидальной сортировки на C++ #include using namespace std; // Процедура для преобразования в двоичную кучу поддерева с корневым узлом i, что является // индексом в arr[]. n - размер кучи void heapify(int arr[], int n, int i) < int largest = i; // Инициализируем наибольший элемент как корень int l = 2*i + 1; // левый = 2*i + 1 int r = 2*i + 2; // правый = 2*i + 2 // Если левый дочерний элемент больше корня if (l < n && arr[l] >arr[largest]) largest = l; // Если правый дочерний элемент больше, чем самый большой элемент на данный момент if (r < n && arr[r] >arr[largest]) largest = r; // Если самый большой элемент не корень if (largest != i) < swap(arr[i], arr[largest]); // Рекурсивно преобразуем в двоичную кучу затронутое поддерево heapify(arr, n, largest); >> // Основная функция, выполняющая пирамидальную сортировку void heapSort(int arr[], int n) < // Построение кучи (перегруппируем массив) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // Один за другим извлекаем элементы из кучи for (int i=n-1; i>=0; i--) < // Перемещаем текущий корень в конец swap(arr[0], arr[i]); // вызываем процедуру heapify на уменьшенной куче heapify(arr, i, 0); >> /* Вспомогательная функция для вывода на экран массива размера n*/ void printArray(int arr[], int n) < for (int i=0; i// Управляющая программа int main() < int arr[] = ; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); cout

      Java

      // Реализация пирамидальной сортировки на Java public class HeapSort < public void sort(int arr[]) < int n = arr.length; // Построение кучи (перегруппируем массив) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // Один за другим извлекаем элементы из кучи for (int i=n-1; i>=0; i--) < // Перемещаем текущий корень в конец int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // Вызываем процедуру heapify на уменьшенной куче heapify(arr, i, 0); >> // Процедура для преобразования в двоичную кучу поддерева с корневым узлом i, что является // индексом в arr[]. n - размер кучи void heapify(int arr[], int n, int i) < int largest = i; // Инициализируем наибольший элемент как корень int l = 2*i + 1; // левый = 2*i + 1 int r = 2*i + 2; // правый = 2*i + 2 // Если левый дочерний элемент больше корня if (l < n && arr[l] >arr[largest]) largest = l; // Если правый дочерний элемент больше, чем самый большой элемент на данный момент if (r < n && arr[r] >arr[largest]) largest = r; // Если самый большой элемент не корень if (largest != i) < int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // Рекурсивно преобразуем в двоичную кучу затронутое поддерево heapify(arr, n, largest); >> /* Вспомогательная функция для вывода на экран массива размера n */ static void printArray(int arr[]) < int n = arr.length; for (int i=0; i// Управляющая программа public static void main(String args[]) < int arr[] = ; int n = arr.length; HeapSort ob = new HeapSort(); ob.sort(arr); System.out.println("Sorted array is"); printArray(arr); > >

      Python

      # Реализация пирамидальной сортировки на Python # Процедура для преобразования в двоичную кучу поддерева с корневым узлом i, что является индексом в arr[]. n - размер кучи def heapify(arr, n, i): largest = i # Initialize largest as root l = 2 * i + 1 # left = 2*i + 1 r = 2 * i + 2 # right = 2*i + 2 # Проверяем существует ли левый дочерний элемент больший, чем корень if l < n and arr[i] < arr[l]: largest = l # Проверяем существует ли правый дочерний элемент больший, чем корень if r < n and arr[largest] < arr[r]: largest = r # Заменяем корень, если нужно if largest != i: arr[i],arr[largest] = arr[largest],arr[i] # свап # Применяем heapify к корню. heapify(arr, n, largest) # Основная функция для сортировки массива заданного размера def heapSort(arr): n = len(arr) # Построение max-heap. for i in range(n, -1, -1): heapify(arr, n, i) # Один за другим извлекаем элементы for i in range(n-1, 0, -1): arr[i], arr[0] = arr[0], arr[i] # свап heapify(arr, i, 0) # Управляющий код для тестирования arr = [ 12, 11, 13, 5, 6, 7] heapSort(arr) n = len(arr) print ("Sorted array is") for i in range(n): print ("%d" %arr[i]), # Этот код предоставил Mohit Kumra

      C Sharp

      // Реализация пирамидальной сортировки на C# using System; public class HeapSort < public void sort(int[] arr) < int n = arr.Length; // Построение кучи (перегруппируем массив) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // Один за другим извлекаем элементы из кучи for (int i=n-1; i>=0; i--) < // Перемещаем текущий корень в конец int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // вызываем процедуру heapify на уменьшенной куче heapify(arr, i, 0); >> // Процедура для преобразования в двоичную кучу поддерева с корневым узлом i, что является // индексом в arr[]. n - размер кучи void heapify(int[] arr, int n, int i) < int largest = i; // Инициализируем наибольший элемент как корень int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 // Если левый дочерний элемент больше корня if (l < n && arr[l] >arr[largest]) largest = l; // Если правый дочерний элемент больше, чем самый большой элемент на данный момент if (r < n && arr[r] >arr[largest]) largest = r; // Если самый большой элемент не корень if (largest != i) < int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // Рекурсивно преобразуем в двоичную кучу затронутое поддерево heapify(arr, n, largest); >> /* Вспомогательная функция для вывода на экран массива размера n */ static void printArray(int[] arr) < int n = arr.Length; for (int i=0; i//Управляющая программа public static void Main() < int[] arr = ; int n = arr.Length; HeapSort ob = new HeapSort(); ob.sort(arr); Console.WriteLine("Sorted array is"); printArray(arr); > > //Этот код предоставил // Akanksha Ra (Abby_akku)

       $arr[$largest]) $largest = $l; //Если правый дочерний элемент больше, чем самый большой элемент на данный момент if ($r < $n && $arr[$r] >$arr[$largest]) $largest = $r; // Если самый большой элемент не корень if ($largest != $i) < $swap = $arr[$i]; $arr[$i] = $arr[$largest]; $arr[$largest] = $swap; // Рекурсивно преобразуем в двоичную кучу затронутое поддерево heapify($arr, $n, $largest); >> //Основная функция, выполняющая пирамидальную сортировку function heapSort(&$arr, $n) < // Построение кучи (перегруппируем массив) for ($i = $n / 2 - 1; $i >= 0; $i--) heapify($arr, $n, $i); //Один за другим извлекаем элементы из кучи for ($i = $n-1; $i >= 0; $i--) < // Перемещаем текущий корень в конец $temp = $arr[0]; $arr[0] = $arr[$i]; $arr[$i] = $temp; // вызываем процедуру heapify на уменьшенной куче heapify($arr, $i, 0); >> /* Вспомогательная функция для вывода на экран массива размера n */ function printArray(&$arr, $n) < for ($i = 0; $i < $n; ++$i) echo ($arr[$i]." ") ; >// Управляющая программа $arr = array(12, 11, 13, 5, 6, 7); $n = sizeof($arr)/sizeof($arr[0]); heapSort($arr, $n); echo 'Sorted array is ' . "\n"; printArray($arr , $n); // Этот код предоставил Shivi_Aggarwal ?>

      Отсортированный массив: 5 6 7 11 12 13

      Здесь предыдущий C-код для справки.

      Замечания:
      Пирамидальная сортировка — это вполне годный алгоритм. Его типичная реализация не стабильна, но может быть таковой сделана (см. Здесь).

      Временная сложность: Временная сложность heapify — O(Logn). Временная сложность createAndBuildHeap() равна O(n), а общее время работы пирамидальной сортировки — O(nLogn).

      Применения пирамидальной сортировки:

      Алгоритм пирамидальной сортировки имеет ограниченное применение, потому что Quicksort (Быстрая сортировка) и Mergesort (Сортировка слиянием) на практике лучше. Тем не менее, сама структура данных кучи используется довольно часто. См. Применения структуры данных кучи

      

      Скриншоты:

      — (Теперь, когда мы построили кучу, мы должны преобразовать ее в max-heap)

      

      — (В max-heap родительский узел всегда больше или равен по отношению к дочерним
      10 больше 4. Поэтому мы меняем местами 4 и 10)
      — (В max-heap родительский узел всегда больше или равен по отношению к дочерним
      5 больше 4. По этому мы меняем местами 5 и 4)

      

      — (Меняем местами первый и последний узлы и удаляем последний из кучи)

      Пожалуйста, оставляйте комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.

      Источник

      Пирамидальная сортировка массива в Java

      Ниже приведен алгоритм пирамидальной сортировки (maxheap) на массиве в Java.

      1. Создание нового узла в конце кучи.
      2. Присвоить новое значение узла.
      3. Сравните значение этого дочернего узла с его родителем.
      4. Если значение родителя меньше, чем у ребенка, а затем поменять их местами.
      5. Повторите шаг 3 до 4 кучного свойство не выполняется.

      Пример

      import java.util.Arrays; import java.util.Scanner; public class Heapsort < public static void heapSort(int[] myArray, int length) < int temp; int size = length-1; for (int i = (length / 2); i >= 0; i--) < heapify(myArray, i, size); >; for(int i= size; i>=0; i--) < temp = myArray[0]; myArray[0] = myArray[size]; myArray[size] = temp; size--; heapify(myArray, 0, size); >System.out.println(Arrays.toString(myArray)); > public static void heapify (int [] myArray, int i, int heapSize) < int a = 2*i; int b = 2*i+1; int largestElement; if (amyArray[i]) < largestElement = a; >else < largestElement = i; >if (b myArray[largestElement]) < largestElement = b; >if (largestElement != i) < int temp = myArray[i]; myArray[i] = myArray[largestElement]; myArray[largestElement] = temp; heapify(myArray, largestElement, heapSize); >> public static void main(String args[]) < Scanner scanner = new Scanner(System.in); System.out.println("Enter the size of the array :: "); int size = scanner.nextInt(); System.out.println("Enter the elements of the array :: "); int[] myArray = new int[size]; for(int i=0; iheapSort(myArray, size); > >

      Итог

      Enter the size of the array :: 5 Enter the elements of the array :: 45 125 44 78 1 [1, 44, 45, 78, 125]

      Средняя оценка 5 / 5. Количество голосов: 1

      Спасибо, помогите другим - напишите комментарий, добавьте информации к статье.

      Видим, что вы не нашли ответ на свой вопрос.

      Напишите комментарий, что можно добавить к статье, какой информации не хватает.

      Источник

      Читайте также:  What does thread mean in java