Permutation with repetition python

Code example for generating permutations with repetition using Python

The swaps between generated permutations are sometimes multiple, as evidenced by the Wikipedia page. Nonetheless, it’s worth noting that the algorithm presented isn’t Heap’s algorithm and doesn’t ensure that a single interchange will result in successive permutations.

How to generate all permutations with repetitions /make x amount of nested for functions

ListA = [0, 1, 2, 3] n = 3 def func(ListA, n): res = [[l] for l in ListA] for i in range(n-1): res = [r+[l] for r in res for l in ListA] return res res_Michael = func(ListA, n) res = [] for i in ListA: for x in ListA: for y in ListA: res.append([i, x, y]) print(res_Michael == res) # True 

res = [[l] for l in ListA]

We should iterate through the elements and concatenate them afterwards.

Due to the initialization of «res», we only concatenate » (n-1) times «.

res = [r+[l] for r in res for l in ListA]

r+[l]

r+[l] means concat list r and [l]

In ListA, number is identified as a member.

is a list with only one element

for r in res for l in ListA

so if wont be for l in ListA for r in res

Python Program to Compute all the Permutation of the, In this example, recursion is used to find the permutations of a string yup.. The if condition prints string passed as argument if it is equal to the length of yub.; In each iteration of the for loop, each character of yup is stored in words.; The elements of words are swapped.

Heap’s algorithm permutation generator

Historical prologue

Since this answer was written, the Wikipedia article on Heap’s algorithm has undergone multiple corrections and defacements. The version mentioned in the question and original answer was erroneous, as can be seen in Wikipedia’s change history. As of March 2022, the current version of the page contains both correct and incorrect versions and it is unclear if it is entirely accurate.

Your code is correct in terms of the implemented Wikipedia pseudocode. You have effectively executed the given algorithm without any errors.

The algorithm that was introduced does not employ Heap’s algorithm and it cannot ensure that consecutive permutations will be produced by a single interchange only. On the Wikipedia page, it is evident that sometimes multiple swaps take place between the generated permutations, as demonstrated in the mentioned lines.

There are three swaps between them, with one of the swaps being a no-operation.

Your code’s output is exactly as expected, as it accurately implements the presented algorithm.

The correct implementation of Heap’s algorithm, and the source of the error

It is noteworthy that the pseudocode is primarily based on Sedgewick’s presentation slides in 2002 (reference 3 on the Wikipedia page and currently accessible on Sedgewick’s website). The erroneous pseudocode can be found on slide 13 and contradicts the preceding slide’s helpful illustration of the algorithm’s operation. After investigating, I discovered numerous instances of this flawed pseudocode, causing me to question my evaluation.

Luckily, I also examined Heap’s concise article (listed as reference 1 on the Wikipedia page), which is quite comprehensible. Heap emphasizes on the following points:

The program follows a standard approach of permuting the first (n — 1) objects and swapping their positions with a designated cell when dealing with n objects. For odd n, the designated cell is always the first cell, whereas for even n, it is numbered sequentially from 1 to (n — 1).

The issue with the presented recursive function is that it always performs a swap before returning, except when N equals 1. This leads to consecutive swaps from 1 to n rather than (n-1) swaps as specified by Heap. As a result, if the function is called with N=3, there will be two swaps at the end of the call before the next yield, one from the end of N=2 call, and the other from the loop with i=N. If N is 4, there will be three swaps, and so on, although some of these swaps may be no-ops.

The algorithm is flawed in its swapping process. Swaps should occur during recursive calls rather than after them. Additionally, it is crucial to avoid any swapping with i==N .

def _heap_perm_(n, A): if n == 1: yield A else: for i in range(n-1): for hp in _heap_perm_(n-1, A): yield hp j = 0 if (n % 2) == 1 else i A[j],A[n-1] = A[n-1],A[j] for hp in _heap_perm_(n-1, A): yield hp 

It is worth noting that the above function was created with the intention of replicating the function with the same name found in the original question. The original function performs an in-place permutation, which saves the expense of copying each permutation that is generated. This makes the full generation O(n!) with a cost of O(1) per permutation generated, instead of O(n·n!) with a cost of O(n) per permutation generated. This approach is suitable if you plan to process each permutation immediately. However, if you intend to keep them around, it can be confusing because the next call to the generator will modify the previous list. In that case, you may want to call the function in a different way.

for perm in map(tuple, heap_perm(n, A)): # Now each perm is independent of the previous one 

Gathering all the codes into an immense list is not advisable due to its enormous size. Instead, consider using something like perms = list(map(tuple, heap_perm(n, A))) to organize them individually.

Sedgewick’s original paper

Upon discovering Sedgewick’s 1977 paper [see note 1], I was thrilled to confirm the accuracy of the algorithm presented. Nevertheless, the usage of a mid-loop test control structure (originally attributed to Donald Knuth) may appear unfamiliar to programmers who primarily work with languages such as Python or C.

Algorithm 1: procedure permutations (N); begin c:=1; loop: if N>2 then permutations(N-1) endif; while c 

On page 141, Sedgewick provides a swap line that modifies Algorithm 1 (on page 140) to align with Heap’s algorithm. Other than this line, the Algorithm remains unaltered. Various versions are also presented.

Notes:

1. At the time of writing my response, the only way to access the paper was through a reference on Wikipedia that required payment. However, it can now be found on Sedgewick’s personal website.

The non-recursive pseudocode from the Wikipedia article about Heap’s algorithm has been converted to Python by me.

A = ['a', 'b', 'c', 'd', 'e', 'f', 'g'] #the initial list to permute n = len(A) #length of A print(A) # output the first permutation (i.e. the original list A itself) number_of_permutations = 1 #a variable to count a number of permutations produced by the script total = [] #a list contaning all generated permutations t = tuple(A) #tuple containing each permutation total.append(t) #adding each permutation to total c = [0] * n #c is the list used to track swapping of positions in each iteration of the Heap`s alrorythm. i = 0 #index of positions in A and c. Serves as a pointer for swapping of positions in A. while i < n: if c[i] < i: # test whether ith position was swapped more than i - 1 times if i % 2 == 0: #swapping the poitions in A A[0], A[i] = A[i], A[0] else: A[c[i]], A[i] = A[i], A[c[i]] print(A) #output of each permutation t = tuple(A) #convert each permutations into unmutable object (tuple) total.append(t) # appending each permutation as tuple in the list of all generated permutations number_of_permutations += 1 #increment number of performed permutations c[i] += 1 # incrementing c[i] is used to indicate that ith position was swapped i = 0 #returns the pointer to the 0th position (imitates recursion) else: c[i] = 0 #when ith position in A was swapped i - 1 times c[i] resets to zero i += 1 #pointer moves to the next position print('Number of permutations generated by the script = ', number_of_permutations) #Examining the correctness of permutions. Total number of permutations should be n! and there should not be any repeates def factorial(n): """ Factorial function""" result = 1 for number in range(1, n + 1): result *= number return result print('Theoretical number of permutations (calculated as n!) = ', factorial(n)) for seq in total: #testing repeates count = total.count(seq) if count >1: x = False else: x = True print('The script does not generates repeats' if x == True else 'The script generates repeats') 

At that place, I implemented a validation test to ensure the accuracy of the output, which verifies the number of unique permutations is equal to n!. The program seems to perform satisfactorily, although my comprehension of its inner workings remains incomplete. Nevertheless, I have included explanatory comments throughout the code based on my current understanding.

The permutations function in the itertools module is the simplest approach to obtain permutations of a list. Therefore, if there are no specific requirements for the algorithm, I would opt for using it.

from itertools import permutations a = [1,2,3,4] for item in permutations(a): print item 

Itertools — Number of permutation with repetition in, from math import factorial from functools import reduce rep= [4,3,5] result= factorial (sum (rep))//reduce (lambda x,y: x*y, map (factorial, rep)) You got 2 options, either you generate them and count them, either you use the formula which gives you the number. If you don’t want any of them, well you can’t do anything.

Permutation without repetition

Display each individual value separated by spaces for every possible combination of the given command line parameters.

import itertools import sys for p in itertools.permutations(sys.argv[1:]): print(" ".join(p)) 

Update

The one-liner below accomplishes the requested task as specified by the OP.

• The echo instruction produces nⁿ permutations separated by spaces, with each permutation’s numbers separated by commas.
• (clearly any way of generating this is fine, as the tricky part is discarding the permutations which have repetitions.)
• The command sed is associated with
• makes the magic with one substitution and
• puts each permutation on a line with the second substitution s/ +/ /g . .

Original answer

The given oneliner is compatible with the initial response that solely employed single-digit numbers.

While I acknowledge the possibility of it being effectively adjusted for use with multi-digit figures, presently, I have no clue.

Algorithm — How to generate permutations without, 3 Answers Sorted by: 1 If your string contains a lot of repeated characters, then you can use a combinations-based algorithm to generate your permutations. Basically, this works by choosing a letter and finding all the places where the duplicates of that letter can go.

Источник

Permutations With Repeating Characters (Python)

The number of combination should be n^k (n=number of elements, k=combination length). For this case, n and k happens to be the same.

ab = 2^2 = 4 abc = 3^3 = 9 If we use `abc`(n=3) to generate permutations of length 1 (k=1) P(abc, 1) = a, b, c = 3^1 = 3 combinations If we use `abc`(n=3) to generate permutations of length 2 (k=2) P(abc, 2) = aa, bb, cc, ab, ac . = 3^2 = 9 combinations

Linear iteration of all elements is unlikely to generate all combinations, so a recursive solution is more likely.

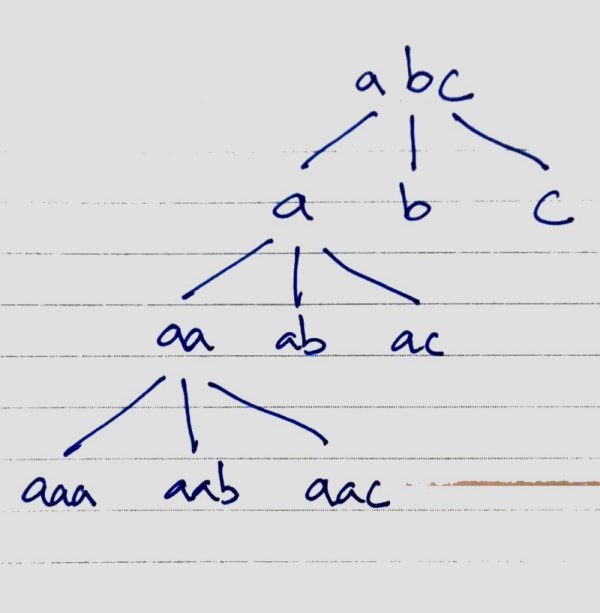
Imagine the following diagram.

Result of P(a) is used to generate P(ab). We start with a prefix of 1 character, then we more character to prefix until all combination are generated recursively.

def _permutation_repeat(text, prefix, n, k): if k == 0: # base, len(prefix) == len(text) print(prefix) return for i in range(n): new_prefix = prefix + text[i] # a, aa, aaa, aab, aac ab, aba, abb, abc # print(new_prefix) _permutation_repeat(text, new_prefix, n, k-1) # print('---') def permutation_repeat(text, k): _permutation_repeat(text, "", len(text), k) permutation_repeat("abc", 3)

The combination is generated in the following sequence.

a -> aa -> aaa aab aac ab -> aba abb abc ac -> aca acb acc b -> ba -> baa bab bac . . 

aaa aab aac aba abb abc aca acb acc baa bab bac bba bbb bbc bca bcb bcc caa cab cac cba cbb cbc cca ccb ccc

Permutation with repeats in result is actually Cartesian Product .

You can use Python itertools.product to generate the same result.

from itertools import product for _set in product(list('abc'), repeat=3): print(''.join(_set))

❤️ Is this article helpful?

Buy me a coffee ☕ or support my work via PayPal to keep this space 🖖 and ad-free.

Do send some 💖 to @d_luaz or share this article.

A dream boy who enjoys making apps, travelling and making youtube videos. Follow me on @d_luaz

Travelopy — discover travel places in Malaysia, Singapore, Taiwan, Japan.

Источник