Перевод системы исчисления питон

ЗаPython’ил ЕГЭ на сотку или почему Python поможет на ЕГЭ

Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!

В сегодняшней статье поговорим о насущной для многих выпускников школ теме — ЕГЭ. Да-да-да! Я знаю, что Хабр — это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.

Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.

Всех желающих — приглашаю ниже!

Быстрый перевод из системы в систему

В Python есть интересные функции bin() , oct() и hex() . Работают данные функции очень просто:

bin(156) #Выводит '0b10011100' oct(156) #Выводит '0o234' hex(156) #Выводит '0x9c'

Как вы видите, выводится строка, где 0b — означает, что число далее в двоичной системе счисления, 0o — в восьмеричной, а 0x — в шестнадцатеричной. Но это стандартные системы, а есть и необычные.

Давайте посмотрим и на них:

n = int(input()) #Вводим целое число b = '' #Формируем пустую строку while n > 0: #Пока число не ноль b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева n = n // 2 #Целочисленное деление print(b) #Вывод

Данная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:

n = int(input()) #Вводим целое число b = '' #Формируем пустую строку while n > 0: #Пока число не ноль if (n % 21) > 9: #Если остаток от деления больше 9. if n % 21 == 10: #. и равен 10. b = 'A' + b #. запишем слева A elif n % 21 == 11:#. и равен 11. b = 'B' + b#. запишем слева B ''' И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20) ''' elif n % 21 == 11: b = 'B' + b elif n % 21 == 12: b = 'C' + b elif n % 21 == 13: b = 'D' + b elif n % 21 == 14: b = 'E' + b elif n % 21 == 15: b = 'F' + b elif n % 21 == 16: b = 'G' + b elif n % 21 == 17: b = 'H' + b elif n % 21 == 18: b = 'I' + b elif n % 21 == 19: b = 'J' + b elif n % 21 == 20: b = 'K' + b else: #Иначе (остаток меньше 10) b = str(n % 21) + b #Остатот от деления записываем слева n = n // 21 #Целочисленное деление print(b) #Вывод

Способ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:

def convert_base(num, to_base=10, from_base=10): # Перевод в десятичную систему if isinstance(num, str): # Если число - строка, то . n = int(num, from_base) # . переводим его в нужную систему счисления else: # Если же ввели число, то . n = int(num) # . просто воспринять его как число # Перевод десятичной в 'to_base' систему alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит if n < to_base: # Если число меньше системы счисления в которую переводить. return alphabet[n] # . вернуть значения номера в алфавите (остаток от деления) else: # Иначе. return convert_base(n // to_base, to_base) + alphabet[n % to_base] # . рекурсивно обратиться к функии нахождения остатка

Вызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).

Задача 2

Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.

Решение данной задачи совсем простое: банальный перебор.

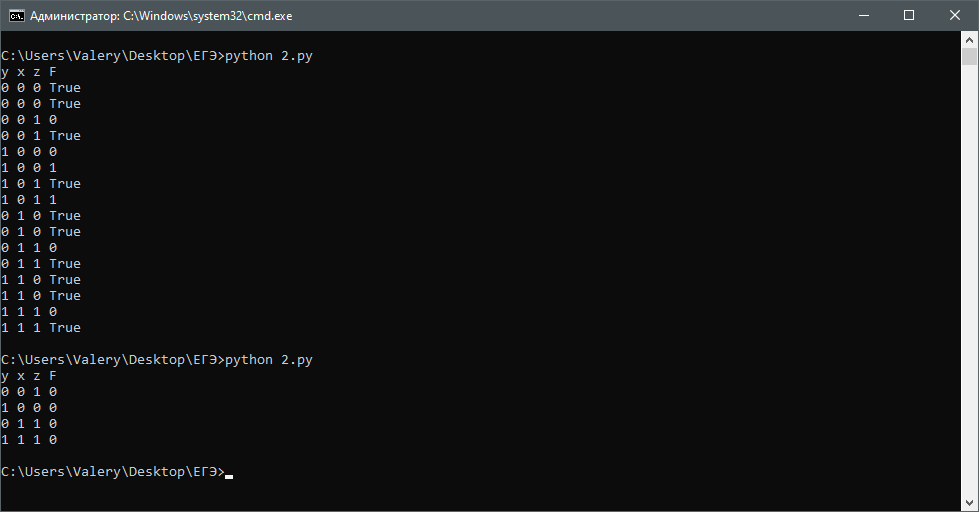
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1' for x in range(2): for z in range(2): for w in range(2): F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию print(x, y, z, F) #Выводим результат

Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:

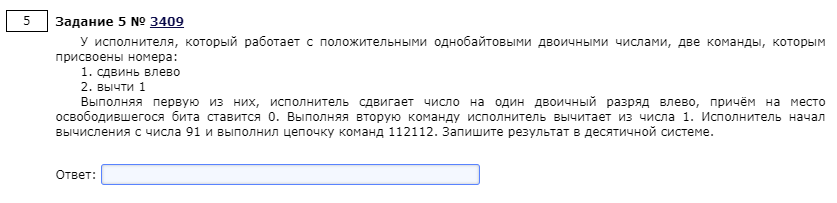
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1' for x in range(2): for z in range(2): for w in range(2): F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию if not F: print(x, y, z, F) #Выводим результат

Задача 5

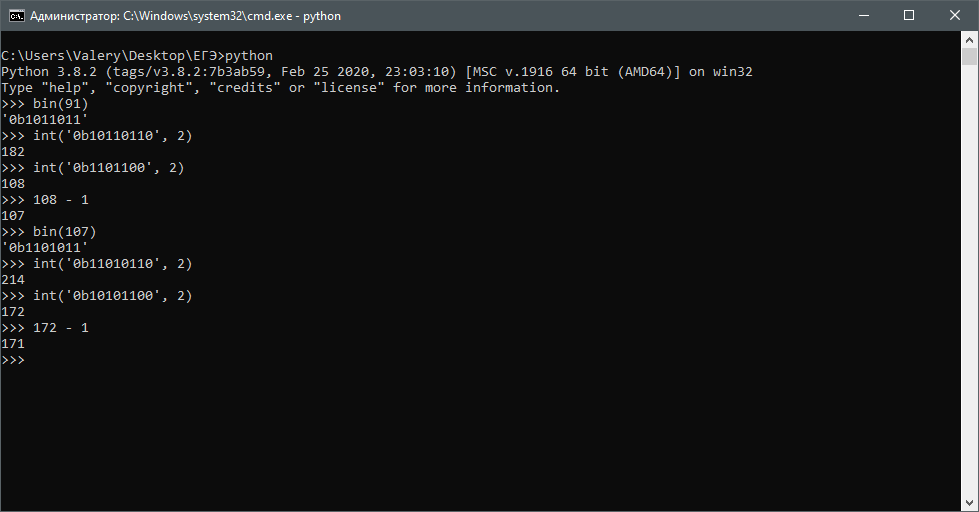
Данная задача легко решается простой последовательностью действий в интерпретационном режиме:

Задача 6

Перепечатали и получили ответ:

Задача 12

В очередной раз, просто заменим слова на код:

a = '9' * 1000 while '999' in a or '888' in a: if '888' in a: a = a.replace('888', '9', 1) else: a = a.replace('999', '8', 1) print(a)

Задача 14

Компьютер железный, он всё посчитает:

a = 4 ** 2020 + 2 ** 2017 - 15 k = 0 while a > 0: if a % 2 == 1: k += 1 a = a // 2 print(k)

Задача 16

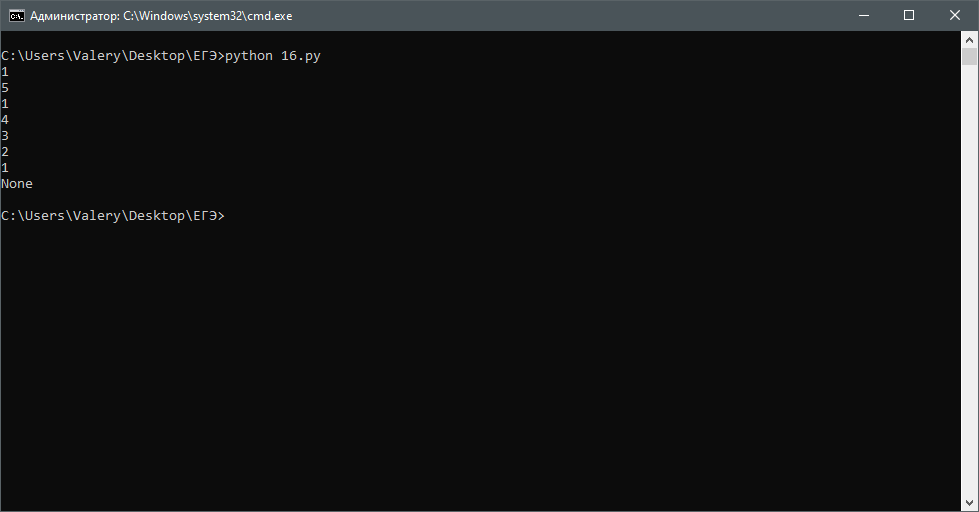
Опять же, просто дублируем программу в python:

def F(n): if n > 0: F(n // 4) print(n) F (n - 1) print(F(5))

Задача 17

Задача с файлом. Самое сложное - достать данные из файла. Но где наша не пропадала?!

with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения text = f.read() #В переменную text запихнули строку целиком a = text.split("\n") #Разбили строку энтерами (\n - знак перехода на новую строку) k = 0 #Стандартно обнуляем количество m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому. for i in range(len(a)): #Обходим все элементы массива if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие k += 1 #Счётчик if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума m = int(a[i - 1]) + int(a[i]) print(k, m) #Вывод

Немного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном - задача стандартна.

Задача 19, 20 и 21

Все три задачи - задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:

Пишем рекурсивную функцию и цикл перебора S:

def f(x, y, p): #Рекурсивная функция if x + y >= 69 or p > 3: #Условия завершения игры return p == 3 return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or\ f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий for s in range (1, 58 + 1): #Перебор S if f(10, s, 1): #Начали с 10 камней print(s) break

Немного пояснений. В рекурсивной функции существует 3 переменные x - число камней в первой куче, y - число камней во второй куче, p - позиция. Позиция рассчитывается по таблице:

Источник

Перевод чисел в Python

В данной статье мы рассмотрим встроенные функции языка программирования Python по переводу чисел в различные системы счисления. А так же напишем универсальную функцию по переводу десятичных чисел в другие системы счисления.

Перевод чисел из десятичной системы счисления
Для перевода числа из десятичной системы счисления в двоичную можно воспользоваться оператором bin(). В качестве аргумента нужно передать значение в виде числа, а оператор вернет строку с двоичным числом. У результата также будет префикс 0b, указывающий на основание системы счисления.

number = 123 result = bin(number) print(result)

Для перевода в восьмеричную систему счисления есть оператор oct(). Он также возвращает строку с восьмеричным числом и префиксом 0o.

number = 123 result = oct(number) print(result)

При переводе в шестнадцатеричную систему счисления воспользуемся оператором hex(). Он вернет строку шестнадцатеричным числом и префиксом 0x

number = 123 result = hex(number) print(result)

Если же вам не нужен префикс у результата перевода, то всегда можно взять срез у полученной строки.

print(bin(123)[2:]) print(oct(123)[2:]) print(hex(123)[2:])

Так же выводить числа в других системах счисления можно используя f-строки и формат вывода. Для этого в строке, через символ : указываем буквы b – для двоичной, o – для восьмеричной и x – для шестнадцатеричной системы счисления.

n = 1984 print(f'Двоичное: ') print(f'Восьмеричное: ') print(f'Шестнадцатеричное: ')

Двоичное: 11111000000 Восьмеричное: 3700 Шестнадцатеричное: 7c0

А теперь напишем универсальную функцию convert_to() по переводу чисел из десятичной системы счисления в систему счисления в любым основанием. Наша функция будет ограничена только наличием символов в переводимой системе счисления.
Данная функция принимает три аргумента, два из которых обязательные. Это десятичное целое число number и основание переводимой системы счисления base. Третий аргумент upper служит для указания регистра вывода строки переведенного числа. По умолчанию он установлен в значение False.

def convert_to(number, base, upper=False): digits = '0123456789abcdefghijklmnopqrstuvwxyz' if base > len(digits): return None result = '' while number > 0: result = digits[number % base] + result number //= base return result.upper() if upper else result

Во второй строке мы задаем переменную digits, содержащую набор символов цифр и букв английского языка. Она нам понадобится для составления символов переведенного числа на основании остатков.
В третьей строке мы проверяем основание переданной системы счисления на его длину. Если основание окажется больше, чем количество символов в нашей строке digits, то мы прекращаем выполнение функции через вызов оператора return и возвращаем None. Это такая своеобразная защита функции от неправильно переданных аргументов. Если мы попробуем перевести число в большую систему счисления по основанию, чем у нас есть символов для его записи, то мы его не сможем записать.
Дальше заведем переменную result для хранения результата работы функции и зададим ей значение в виде пустой строки. Теперь с помощью цикла с условием будем находить остаток от деления числа number на основание base, а также уменьшать number в base раз используя целочисленное деление.
Остаток от деления числа на основание переводимой системы счисления мы будем использовать как индекс для получения символа в строке digits и добавлять его к результату result. Добавлять это значение следует слева, т.к. самый первый остаток является самым правым разрядом. Цикл выполняется до тех пор, пока исходное значение переменной number больше нуля.
После завершения цикла мы вернем результат через вызов return. Для этого воспользуемся тернарным оператором и проверим наш третий аргумент. Если он будет в значении True, то для строки result вызовем строкой метод .upper() который заменит все прописные символы английского языка на строчные. Иначе, вернем результат как есть.

А теперь проверим работу нашей функции. Для этого попробуем перевести числа в 2ю, 8ю, 16ю, 32ю и 64ю системы счисления. Для перевода в 32ю систему счисления мы укажем третий необязательный аргумент upper и зададим ему значение True.

print(convert_to(123, 2)) print(convert_to(123, 8)) print(convert_to(123, 16)) print(convert_to(123, 32, upper=True)) print(convert_to(123, 64))

Перевод чисел в десятичную систему счисления
Для обратного перевода в десятичную систему счисления мы будем использовать оператор int(). Для этого передадим ему два аргумента, первый – это строка с числом в какой-то системе счисления, а второй – это основание системы счисления самого числа. По умолчанию для этого необязательного аргумента стоит значение равное 10.
В качестве самого числа нужно обязательно передать строку. Строка может содержать или само число или число с префиксом системы счисления.
Для перевода из двоичной системы счисления:

number = '11001' result = int(number, 2) print(result)

number = '0b11001' result = int(number, 2) print(result)

Для перевода из восьмеричной системы счисления:

Источник