Python находит временные интервалы пересечения в массиве
У меня есть массив питонов с двумя строками. Одна строка описывает время начала события, а другая описывает конец (здесь времена как целые числа эпох). Пример кода означает, что событие с индексом = 0 начинается в момент времени = 1 и заканчивается в момент времени = 7.
start = [1, 8, 15, 30] end = [7, 16, 20, 40] timeranges = np.array([start,end]) Я хочу знать, пересекаются ли временные диапазоны. Это означает, что мне нужна функция / алгоритм, который вычисляет информацию, что временной диапазон от 8 до 16 пересекается с временным диапазоном от 15 до 20.
Мое решение состоит в том, чтобы использовать два пересекающихся цикла и проверить, находится ли какое-либо время начала или окончания в другом диапазоне времени. Но с ipython это длится очень долго, потому что мои временные диапазоны заполнены почти 10000 событиями.
Есть ли элегантное решение, чтобы получить результат за «короткое» время (например, менее одной минуты)?
2 ответа
Сохраните данные как коллекцию (time,index_in_list,start_or_end) . Например, если входные данные:
start = [1, 8, 15, 30] end = [7, 16, 20, 40] Преобразуйте входные данные в список кортежей следующим образом:
def extract_times(times,is_start): return [(times[i],i,is_start) for i in range(len(times))] extract_times(start,true) == [(1,0,true),(8,1,true),(15,2,true),(30,3,true)] extract_times(end,false) == [(7,0,false),(16,1,false),(20,2,false),(40,3,false)] Теперь объедините два списка и сохраните их. Затем начинайте обход списков от начала до конца, каждый раз отслеживая текущие пересекающиеся интервалы, обновляя состояние в зависимости от того, является ли каждый новый кортеж началом или концом интервала. Таким образом, вы найдете все совпадения.
Сложность O(n log(n)) для сортировки плюс некоторые издержки, если есть много пересечений.
Учитывая, что входные списки могут не сортироваться и обрабатывать случаи, когда мы можем видеть временные интервалы с несколькими пересечениями, вот метод, основанный на грубом сравнении, использующий broadcasting —
np.argwhere(np.triu(timeranges[1][:,None] > timeranges[0],1)) Примеры прогонов
In [81]: timeranges Out[81]: array([[ 1, 8, 15, 30], [ 7, 16, 20, 40]]) In [82]: np.argwhere(np.triu(timeranges[1][:,None] > timeranges[0],1)) Out[82]: array([[1, 2]]) Случай нескольких пересечений:
In [77]: timeranges Out[77]: array([[ 5, 7, 18, 12, 19], [11, 17, 28, 19, 28]]) In [78]: np.argwhere(np.triu(timeranges[1][:,None] > timeranges[0],1)) Out[78]: array([[0, 1], [1, 3], [2, 3], [2, 4]]) Если под within в «if any start time or end time is within an other timerange» вы подразумевали, что границы являются инклюзивными, измените сравнение > на > в коде решения.
Задачка на пересечение интервалов
Ребят помогите пожалуйста советом как решить задачу, 2 дня без сна.
_____________________________________________________________
Коля хочет собрать друзей у себя, чтобы решить, куда они поедут отдыхать в выходные. В компании Коли полная демократия, решение принимается большинством голосов. Среди друзей есть очень ленивые люди, и они доверили свой голос кому-то из компании. Каждый написал Коле промежутки времени, когда он сможет явиться в единую точку голосования и сколько людей ему доверили проголосовать за них. Друзья у Коли работают очень слаженно и могут принять решение за очень маленький промежуток времени, даже когда один из них только явился на встречу, а второй уже будет уходить.
Помогите Коле понять, какое максимальное количество голосов он сможет собрать, если выберет оптимальное время.
На вход подается файл, где в первой строке написано количество друзей, от которых поступила информация. В каждой следующей строке имеется информация про одного друга Коли через пробел: время, когда он сможет прийти, время, когда ему нужно будет уходить, сколько друзей доверили ему свой голос. Все числа целые, неотрицательные и меньше 32 767.
На выходе нужно вывести максимальное количество голосов, которое сможет собрать Коля, выбрав оптимальное время.
Мое решение такое:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
n = int(input('количество друзей: ')) s = [] A = [] B = [] my_friends = range(n) for i in my_friends: a = int(input('время прихода: ')) b = int(input('время ухода: ')) c = int(input('количество голосов: ')) if i == 0: A.append(a) B.append(b) if c == 0: s.append(1) else: s.append(1 + c) else: if b >= min(A) and a max(B): A.append(a) B.append(b) if c == 0: s.append(1) else: s.append(1 + c) else: continue print(sum(s))
______________________________
Код работает но не решает полностью задачу. так например он не находит ту оптимальную точку времени когда интервалы времени каждого из друзей пересекаются хотя бы в 1 точке.
пересечение интервала даты Python
В целом меня интересует, есть ли более элегантный/эффективный способ сделать это. У меня есть функция, которая сравнивает два стартовых/конечных кортежа дат, возвращающих true, если они пересекаются.
from datetime import date def date_intersection(t1, t2): t1start, t1end = t1[0], t1[1] t2start, t2end = t2[0], t2[1] if t1end < t2start: return False if t1end == t2start: return True if t1start == t2start: return True if t1start < t2start and t2start < t1end: return True if t1start >t2start and t1end < t2end: return True if t1start < t2start and t1end >t2end: return True if t1start < t2end and t1end >t2end: return True if t1start > t2start and t1start < t2end: return True if t1start == t2end: return True if t1end == t2end: return True if t1start >t2end: return False d1 = date(2000, 1, 10) d2 = date(2000, 1, 11) d3 = date(2000, 1, 12) d4 = date(2000, 1, 13) >>> date_intersection((d1,d2),(d3,d4)) False >>> date_intersection((d1,d2),(d2,d3)) True >>> date_intersection((d1,d3),(d2,d4)) True и др. Мне интересно узнать, есть ли более pythonic/элегантный/более эффективный/менее подробный/вообще лучше, способ сделать это, возможно, с mxDateTime или какой-нибудь умный взлом с timedelta или set()? Альтернативной и полезной формой будет функция, чтобы вернуть начальный/конечный кортеж пересечения, если он найден Спасибо
Вы должны использовать timedelt для представления длительностей t1 ⇔ t2 и я думаю о следующем бите. docs.python.org/library/datetime.html#datetime.timedelta
Вычисление пересекающихся интервалов в линейных и замкнутых пространствах имен
Здравствуйте! И сразу прошу прощение, за слишком мудрёное название, но оно наиболее полно отражает излагаемый ниже материал.
Я думаю многие из вас сталкивались с необходимостью вычисления пересекающихся интервалов. Но задача с которой я столкнулся на днях — оказалась не столь тривиальной. Но, обо всем по порядку.
Вычисление пересекающихся интервалов в линейном пространстве имен
Если у вас уже есть представление о пересечении интервалов, то пройдите сразу сюда.
Вычисление пересечений временных интервалов (отрезков времени) на прямой линии времени не составляет особого труда. Мы можем условно иметь пять видов временных пересечений.
Обозначим один отрезок времени как «\ \», а другой «/ /»
- Смещение вперед по оси времени «/ \ / \»
- Смещение назад по оси времени «\ / \ /»
- Вхождение » / \ \ / «
- Поглощение «\ / / \ «
- Совпадение «X X»
SET @start:=4; SET @end:=8; SELECT * FROM `table` WHERE (`start` >= @start AND `start` < @end) /*смещение вперед*/ OR (`end` @start) /*смещение назад*/ OR (`start` < @end AND `end` >@start) /*вхождение - на самом деле здесь не обязательно оно обработается одним из предыдущих выражений*/ OR (`start` >= @start AND `end` Данный запрос вернет первого, второго и третьего пользователей. Всё довольно просто.
SET @start:=4; SET @end:=8; SELECT * FROM `table` WHERE `start` >= @end OR `end` И вот тут мы вспоминаем про отрицания выражений. Если вычислять непересечения намного проще чем пересечения, то почему бы просто не отбросить все непересечения?
WHERE NOT ( `start` >= @end OR `end` Вуа-ля! Все намного лаконичнее!
Всё это очень прекрасно, и замечательно работает… пока линия времени прямая.
Вычисление пересекающихся интервалов в замкнутых пространствах имен
С вычислениями на линии времени мы разобрались. Так что же такое «замкнутое» пространство имен?
Это такое пространство имен, которое, при исчерпании имён первого порядка, не переходит на новый порядок а возвращается к своему началу.
Линейное пространство имен:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,…
Замкнутое пространство имен:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4,…
Предположим, что у нас есть таблица с расписанием графика работы (пусть это будет круглосуточный колл-центр):
*минуты «00» опущены для простоты выражений
| usrer | start | end |
| usrer1 | 0 | 6 |
| usrer2 | 6 | 12 |
| usrer3 | 12 | 18 |
| usrer4 | 18 | 23 |
Я работаю с 10 до 19 и хочу знать какие именно работники будут пересекать мой график работы.
Делаем выборку, заданной ранее схеме:
SET @start:=10; SET @end:=19; SELECT * FROM `table` WHERE NOT ( `start` >= @end OR `end` Все отлично! Я получил данные трёх работников, чей интервал пересекается с моим.
Ок, а если я работаю в ночь? Допустим с 20 до 6? То есть начало моего интервала больше его конца. Выборка из таблицы по этим условиям вернет полную ахинею. То есть крах случается, когда мой временной интервал пересекает «нулевую» отметку суток. Но ведь и в базе могут хранится интервалы пересекающие «нулевую» отметку.
С подобной проблемой я столкнулся два дня назад.
Проблема выборки интервалов по линейной методике из таблицы с данными нелинейной структуры была на лицо.
Первое, что мне пришло в голову — это расширить пространство суток до 48 часов, тем самым избавляясь от «нулевой» отметки. Но эта попытка потерпела крах — потому что интервалы между 1 и 3 никак не могли попасть в выборку между 22 и 27(3). Эх! Вот если бы у меня была двадцати-четыричная система счисления, я бы просто убирал знак второго порядка и все дела.
Я предпринял попытку найти решение этой проблемы в интернете. Информации по пересечению интервалов на «линейном» времени было сколько угодно. Но то ли этот вопрос не имел широкого обсуждения, то ли гуру SQL держали решение «для себя» — решения по замкнутой системе нигде небыло.
В общем, поспрашивав на форумах советов от гуру, я получил решение: нужно было разбить пересекающие «ноль» интервалы на две части, тем самым получив два линейных интервала, и сравнивать их оба с интервалами в таблице (которые тоже нужно было разбить на две части, если они пересекают ноль). Решение работало и вполне стабильно, хоть и было громоздким. Однако меня не покидало ощущение, что всё «намного проще».
И вот, выделив пару часов для этого вопроса, я взял тетрадь и карандаш… Привожу то, что у меня получилось: 
Суть в том, что сутки — есть замкнутая линия времени — окружность.
А временные интервалы — суть дуги этой окружности.
Таким образом, мы для отрицания непересечений (см. первую часть поста), можем построить пару схем непересечения: 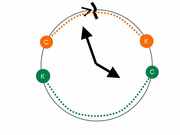
В первом случае мы имеем обычную линейную схему для отрицания непересечений. Во втором одна из дуг пресекает «нулевую» отметку. Есть и третий случай, который можно сразу принять как пересечение ( без отрицаний непересечения ): 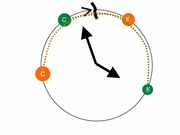
Немного наколдовав с базой (где-то даже методом высоконаучного тыка), мне удалось собрать вот такой запрос:
SET @start:= X ; SET @end:= Y; SELECT * FROM `lparty_ads` WHERE ((`prime_start` < `prime_end` AND @start < @end) AND NOT (`prime_end`@end) OR (`prime_start` > `prime_end` AND @start < @end)) AND NOT ( `prime_end` `prime_end` AND @start > @end)) И упрощенный вариант из комментария от kirillzorin:
set @start := X; set @end := Y; select * from tab where greatest(start, @start) @start or @end > start) and sign(start - end) <> sign(@start - @end)) or (end < start and @end < @start); Запрос вполне работоспособен и, что самое забавное, справедлив для любых замкнутых систем счисления — будь то час, сутки, неделя, месяц, год. А еще, этот метод не использует «костылей», вроде дополнительных полей.
Скорее всего, я изобрёл велосипед. Но ввиду того, что сам я не нашел подобной информации, когда она мне понадобилась — предполагаю, что этот метод не слишком широко освещен. На этом моё повествование заканчивается.
