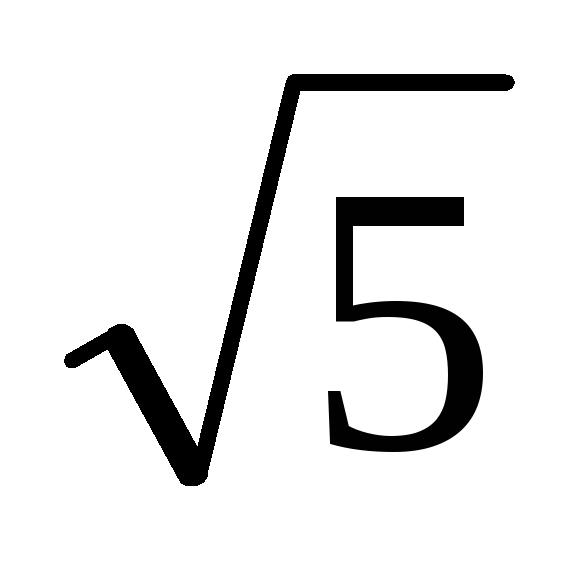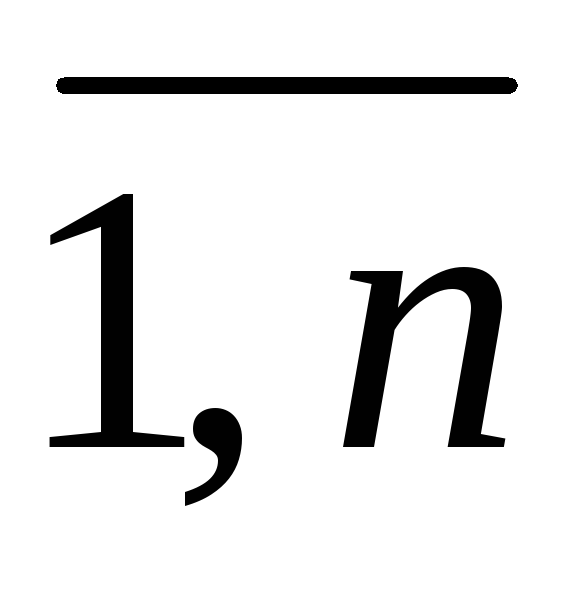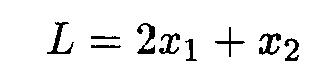Отличие задачи нелинейного программирования от линейного

Нелинейное программирование Общая постановка задачи

где x_j – переменные, — заданные функции от п переменных, b_i – фиксированные значения.

Для задачи нелинейного программирования в отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, приближённые методы решения, графический метод.

Графический метод

Рассмотрим примеры решение задач нелинейного программирования с двумя переменными, причём их целевые функции и системы ограничений могут быть заданы в линейном и нелинейном виде. Так же как и в задачах линейного программирования, они могут быть решены графически.

Задача с линейной целевой функцией и нелинейной системой ограничений

Пример 1. Найти глобальные экстремумы функции

ОТВЕТ. Глобальный минимум, равный нулю, достигается в точке О(0, 0), глобальный максимум, равный , — в точке

Задача с нелинейной целевой функцией и линейной системой ограничений

Пример 2. Найти глобальные экстремумы функции

ОТВЕТ. Глобальный максимум, равный 58, достигается в точке D(9, 0), глобальный минимум, равный нулю, — в точке О₁(2, 3).

Пример 3. Найти глобальные экстремумы функции

ОТВЕТ. Глобальный максимум, равный 52, находится в точке О(0, 0). Глобальный минимум, равный 1053/169, находится в точке Е(51/13б21/13).

Задача с нелинейной целевой функцией и нелинейной системой ограничений

Пример 4. Найти глобальные экстремумы функции

ОТВЕТ. Глобальный минимум, равный нулю, достигается в точке О₁(2, 1), глобальный максимум, равный 13, находится в точке А(0, 4).

Пример 5. Найти глобальные экстремумы функции

ОТВЕТ. Целевая функция имеет два глобальных минимума, равных 17, в точках А(1, 4) и В(4, 1), глобальный максимум, равный 2417/49, достигается в точке Е(7, 4/7).

Дробно-линейное программирование

Дробно-линейное программирование относится к нелинейному программированию, так как имеет целевую функцию, заданную в нелинейном виде.

Задача дробно-линейного программирования в общем виде записывается следующим образом:

где — постоянные коэффициенты и

Рассмотрим задачу дробно-линейного программирования в виде

Для решения этой задачи найдём область допустимых решений, определяемую заданными ограничениями. Пусть эта область не является пустым множеством.

Из выражения, задающего целевую функцию, найдём х₂:

Прямая x₂ = kx₁ проходит через начало координат. При некотором фиксированном значении L угловой коэффициент k тоже фиксирован, и прямая займёт определённое положение. При изменении значений L прямая x₂ = kx₁ будет поворачиваться вокруг начала координат.

Установим, как будет вести себя угловой коэффициент k при монотонном возрастании L. Найдём производную от k по L:

Знаменатель производной всегда положителен, а числитель от L не зависит. Следовательно, производная имеет постоянный знак, и при увеличении L угловой коэффициент будет только возрастать или только убывать, а прямая будет поворачиваться в одну сторону. Если имеет положительное значение, то прямая вращается против часовой стрелки, при отрицательном значении — по часовой стрелке. Установив направление вращения, находим вершину или вершины многогранника, в которых функция принимает max (min) значение, либо устанавливаем неограниченность задачи.

При этом возможны следующие случаи.

1. Область допустимых решений ограничена, максимум и минимум достигаются в её угловых точках (рис. а).

2. Область допустимых решений неограниченна, однако существуют угловые точки, в которых целевая функция принимает максимальное и минимальное значения (рис. б).

3. Область допустимых решений неограниченна, имеется один из экстремумов. Например, минимум достигается в одной из вершин области и имеет так называемый асимптотический максимум (рис. в).

4. Область допустимых решений неограниченна. Максимум и минимум являются асимптотическими (рис. г).

Источник

3. Краткая характеристика экономико-математических методов

Линейное программирование применяется для нахождения опти­мальных решений многих экономических задач. Оно основано на реше­нии системы уравнений и неравенств при функциональной зависимости рассматриваемых процессов. Сформулированная функция цели позво­ляет выбрать из большого числа альтернативных вариантов лучший, оптимальный.

Термин «программирование» связан с тем, что неизвестные перемен­ные, которые отыскиваются в процессе решения, обычно определяют лучший вариант плана деятельности некоторого экономического объек­та. Следует однако иметь в виду, что предпосылка линейности, лежащая в основе этого метода, — существенное огрубление реальной ситуации, которая, как правило, носит более сложный нелинейный характер.

Нелинейное программирование

Предлагает методы решения таких задач, в которых результаты изме­няются непропорционально масштабу производства. В отличие от ли­нейного программирования здесь заранее не оговаривается форма ни неравенств, ни целевой функции. Поэтому могут быть различные вари­анты их сочетаний: целевая функция нелинейна, а ограничения линей­ны; целевая функция линейна, а ограничения нелинейны; и целевая функ­ция, и ограничения нелинейны.

В связи со сложностями решения задач нелинейного программиро­вания их упрощают тем, что сводят к линейным: условно принимают, что на том или ином участке целевая функция возрастает или убывает пропорционально изменению независимых переменных (метод кусоч­но-линейных приближений).

Дискретное (целочисленное) программирование

Этот раздел математического программирования накладывает на ис­комые переменные дополнительное ограничение их целочисленности. Такое ограничение отвечает требованию очень большого числа эконо­мических задач. Оно во многом связано с физической неделимостью факторов и объектов расчета. Например, судостроительное предприя­тие не может построить 2,38 готового судна. Кроме того, требование целочисленности может относиться и к определенным периодам деятель­ности предприятия. Дискретными являются решения таких известных задач исследования операций, как задача о коммивояжере, задача о на­значениях, задача теории расписаний, задача замены оборудования и др.

Самым простым способом решения задач дискретного программиро­вания — это решение их одним из способов линейного программирова­ния, например, симплекс-методом, проверкой полученного результата на целочисленность и последующим округлением, что может, естественно, сделать полученные итоги отличными от оптимального уровня.

Динамическое программирование

Раздел математического программирования, основанный на пошаго­вом решении задачи, вычислении последствий каждого шага и принятии оптимальной стратегии для последующих шагов. Таким образом, динамическое программирование — это многошаговый процесс. Напри­мер, полученные экономические параметры данного периода являются основанием для построений последующего.

Такой многошаговый процесс не обязательно должен быть связан со временем. Он может быть и статическим, например, задача обновления оборудования на предприятии.

Поэтапность схемы динамического программирования накладывает на критерий оптимальности требование аддитивности, т. е. общее опти­мальное решение является суммой оптимальных решений каждого шага.

Область применения метода динамического программирования — это планирование деятельности экономического объекта, распределе­ние ресурсов во времени и на различные цели, ремонт и замена оборудо­вания.

Источник

ЛИНЕЙНОЕ И НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Линейное программирование. Этот метод математического программирования объединяет методы решения задач, которые описываются линейными уравнениями. Если предприятие работает на рынке, близком по свойствам к рынку чистой конкуренции, на котором оно вынуждено продавать товары по неизменной, установившейся независимо от предприятия цене, то между выручкой от реализации, издержками и количеством реализованной продукции может существовать линейная зависимость. Ограничения выпуска продукции по загрузке производственных мощностей выпускаемой продукции могут быть описаны линейными неравенствами. В этом случае составление оптимального по прибыли или выручке от реализации плана производства сводится к решению задачи линейного программирования.

Нелинейное программирование. Оно объединяет методы решения задач, которые описываются нелинейными соотношениями. К задачам нелинейного программирования относятся задачи оптимизации производства для большинства предприятий, поскольку в настоящее время они действуют на неоднородном рынке в условиях монополистической конкуренции и спрос на их продукцию зависит от цены.

Оптимизация по максимуму выручки или прибыли. Предприятие, действующее на неоднородном рынке, или предприятие-монополист может легко использовать этот метод, если связь цены и сбыта представить линейной функцией. Выручка от реализации определяется так:

где ВВ — валовая выручка; P_j — цена /’-го вида продукции; Q, — объем производства и реализации /-го вида продукции; а_; и Ь₍ — постоянные коэффициенты линейной зависимости цены соответственно от объема производства и сбыта /-го вида продукции; /’ — порядковый номер вида продукции; п — общее число видов продукции, которую предполагается производить в планируемом периоде; Е_/=, — суммы по всем п видам продукции.

Прибыль предприятия определяется так:

где ВИ — валовые издержки; ПОИ — постоянные издержки; СПИ — средние переменные издержки в производстве /’-го вида продукции.

Из (1) вытекает целевая функция для максимизации выручки:

Из (2) вытекает целевая функция для максимизации прибыли:

Источник

28.1. Общая постановка задачи

Математическая модель задачи нелинейного программиро­вания в общем виде формулируется следующим образом: найти вектор = (х₁, x₂, …, x_n), удовлетворяющий системе ограни­чений

и доставляющий экстремум (наибольшее или наименьшее зна­чение) целевой функции

где x_j — переменные, j = ;L, f, g_i — заданные функции от n переменных, b_i — фиксированные значения.

Нелинейное программирование применяется при прогнози­ровании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудова­ния и т.д.

Для задачи нелинейного программирования в отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программи­рование, градиентные методы, приближенные методы реше­ния, графический метод.

Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная. Однако даже для таких задач оптималь­ное решение может быть найдено для определенного класса це­левых функций. Например, когда целевая функция сепарабельная, т.е. является суммой п функций f_j(x_j), или квадратичная. При этом следует отметить, что в отличие от задач линейного программирования, где точками экстремума являются верши­ны многогранника решений, в задачах с нелинейной целевой функцией точки могут находиться внутри многогранника, на его ребре или в вершине.

При решении задач нелинейного программирования для це­левой функции необходимо определить глобальный максимум или глобальный минимум. Глобальный максимум (минимум) функции — это ее наибольшее (наименьшее) значение из ло­кальных максимумов (минимумов).

Наличие локальных экстремумов затрудняет решение за­дач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найден­ный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять ло­кальный экстремум, который может существенно отличаться от глобального.

28.2. Графический метод

Рассмотрим примеры решения задач нелинейного програм­мирования с двумя переменными, причем их целевые функции и системы ограничений могут быть заданы в линейном и не­линейном виде. Так же как и в задачах линейного программи­рования, они могут быть решены графически.

Задача с линейной целевой функцией и нелинейной системой ограничений

Пример 1. Найти глобальные экстремумы функции

Решение. Область допустимых решений — часть окруж­ности с радиусом 4, которая расположена в первой четверти (рис. 28.1).

Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2. Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем че­рез точку А прямую, перпендикулярную линии уровня. Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение x₂ = 1/2х₁.

откуда находим х₁ = 8/5,x₂ = 4/5, L = 16/5 + 4/5 = 4.

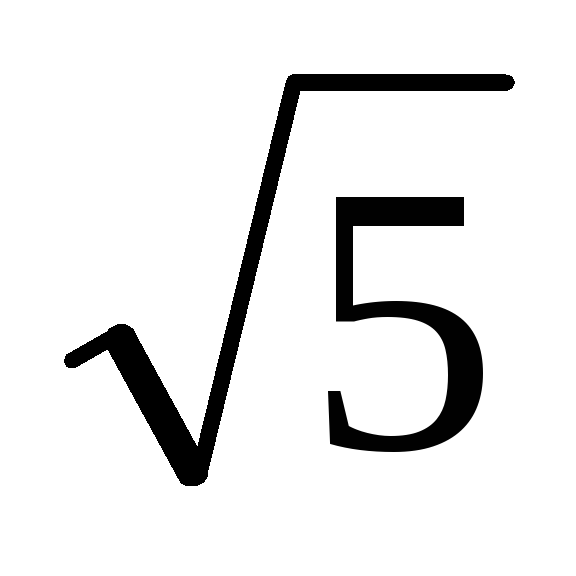
Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4, — в точкеА(8/5, 4/5).

Источник