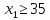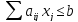Особенности задач математического программирования

1. Определение задачи математического программирования

Математическое программирование — это область математики, разрабатывающая теорию, решения многомерных задач с ограничениями. В отличие от классической математики, мы находим наилучший вариант из всех возможных.

Итак, математическое программирование — это раздел высшей математики, занимающийся решением задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.

Общая задача М. п. состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

Классическая задача математического программирования – задача выбора таких значений некоторых переменных, подчиненных системе ограничений в форме равенств, при которых достигается max или min функции.

2. Допустимое решение задачи, одр, оптимальное решение задачи.

Допустимым решением задачи называется любой n-мерный вектор

x (x = (,,…,)), удовлетворяющий системе ограничений и условию неотрицательности.

Множество допустимых решений образует ОДР.

Оптимальным решением задачи называется такое допустимое решение, при котором целевая функция достигает экстремума.

3. Экономико–математические модели задач лп: задача о банке

К экономико-математическим моделям задач ЛП относятся:Задача планирования производства, определения оптимального ассортимента продукции, о диете, о банке, составления жидких смесей, Транспортная задача

Построение экономико – математической модели.

Задача о банке

Собственные средства банка в сумме с депозитами составляют 100 млн. $. Не менее 35 млн. $ из этой суммы размещена в кредитах (не ликвид). Ликвидное ограничение ценных бумаг должны составлять не менее 30 %, размещенных в кредитах и ликвидных активах.

Пусть 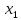— средства, размещенные в кредитах,– средства, размещенные в ликвидных активах.

Банк. Огран. (1)

Кред. Огран.

Ликвид. Огран.

Условие неопределенности ,≥0 (4)

— доходность кредитов, — доходность ликвидных активов

F = при услов. (1) – (4).

4. Экономико – математические модели задач лп: задача определения оптимального ассортимента продукции.

— П1, — П2

F = 3

2

3

5. Задача лп, стандартная форма, каноническая форма.

К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

В общем виде модель записывается следующим образом:

Целевая функция: F (x)= c1x1 + c2x2 + . + cnxn → max(min)

ограничения: a11x1 + a12x2 + . + a1nxn b1,

требование неотрицательности: xj ≥ 0,

Задача имеет каноническую форму, если является задачей на максимум (минимум) линейной функции F и ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х1, х2, . хn являются неотрицательными:

F (x) =

, i= 1,2…m

, j = 1,2…n

В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной функции f и система ограничений ее состоит из одних линейных неравенств типа «

F (x) =

, i= 1,2…m

, j = 1,2…n

Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.

Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации — ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.

Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума)

Источник

Постановка задачи и методы математического программирования.

Математическая постановка (модель) задачи математического программирования (МП) выглядит следующим образом:

необходимо определить значения вектора переменных

x = (x₁,x₂,…, x_n), которые удовлетворяют ограничениям вида

g _i (x₁,x₂,…, x_n) b_i , для всех i = 1,…, m

и доставляют максимум или минимум целевой функции

f (x₁,x₂,…, x_n) → max (min).

Решением (планом, вектором управления) задачи МП называется всякий вектор х из пространства E n (E n — n-мерное векторное пространство), в геометрической интерпретации – это точка векторного n-мерного пространства. Допустимым решением (планом) задачи МП называется такое решение задачи, которое удовлетворяет ее ограничениям g _i (x₁,x₂,…,x_n) b_i , для всех i = 1,…, m.

Совокупность допустимых решений задачи называют областью допустимых решений (ОДР) задачи МП, которую, как правило, обозначают как D. Оптимальным решением х*называется такое допустимое решение, при котором целевая функция достигает своего оптимального (в нашем случае — максимального) значения, т. е. решение, удовлетворяющее условию max f(x) = f(x*). Величина f* = f(x*) называется оптимальным значением целевой функции.

Окончательным решением задачи является пара (х*, f*), состоящая из оптимального решения и оптимального значения целевой функции

Постановка задачи и методы стохастического программирования

При перспективном и оперативном планировании работы предприятия возникает необходимость в учете ряда случайных факторов, существенно влияющих на процесс производства. К таким факторам относятся спрос, который не всегда может быть предсказуем, непредусмотренные сбои в поступлении сырья, энергии, рабочей силы, неисправности и аварии оборудования. Еще больше случайных факторов необходимо учитывать при планировании производства, эффективность которого зависит от климатических условий, урожайности и т.д. Поэтому, например, задачи планирования лесного производства целесообразно ставить и исследовать в терминах и понятиях стохастического программирования, когда элементы задачи линейного программирования (матрица коэффициентов A, вектора ресурсов b, вектора оценок c) часто оказываются случайными. Подобного типа задачи ЛП принято классифицировать как задачи стохастического программирования (СП).

Подходы к постановке и анализу стохастических задач существенно различаются в зависимости от последовательности получения информации — в один прием или по частям. При построении стохастической модели важно также знать, необходимо ли принять единственное решение, не подлежащее корректировке, или можно по мере накопления информации один или несколько раз корректировать решение. В соответствии с этим в стохастическом программировании исследуются одноэтапные, двухэтапные и многоэтапные задачи.

В одноэтапных задачах решение принимается один раз и не корректируется. Они различаются по показателям качества решения (по целевым функциям), по характеру ограничений и по виду решения.

Задача СП может быть сформулирована в M- и P- постановках по отношению к записи целевой функции и ограничений.

Случайны элементы вектора с (целевая функция).

При M-постановке целевая функция W записывается в виде

что означает оптимизацию математического ожидания целевой функции. От математического ожидания целевой функции можно перейти к математическому ожиданию случайной величины c_j

W_min — предварительно заданное допустимое наихудшее (минимальное) значение целевой функции.

W_max — предварительно заданное допустимое наихудшее (максимальное) значение целевой функции.

Суть P-постановки заключается в том, что необходимо найти такие значения x_j, при которых максимизируется вероятность того, что целевая функция будет не хуже предельно допустимого значения.

Ограничения задачи, которые должны выполняться при всех реализациях параметров условий задачи, называются жесткими ограничениями. Часто возникают ситуации, в которых постановка задачи позволяет заменить жесткие ограничения их усреднением по распределению случайных параметров. Такие ограничения называют статистическими:

В тех случаях, когда по содержательным соображениям можно допустить, чтобы невязки в условиях не превышали заданных с вероятностями, небольшими  _i>0, говорят о стохастических задачах с вероятностными ограничениями:

т.е. вероятность выполнения каждого заданного ограничения должна быть не менее назначенной величины  _i. Параметры  _i предполагаются заданными или являются решениями задачи более высокого уровня.

Представленные задачи как в M-, так и в P- постановках непосредственно решены быть не могут. Возможным методом решения этих задач является переход к их детерминированным эквивалентам. В основе этого перехода лежит использование закона распределения случайной величины. В инженерной практике наиболее часто используется нормальный закон распределения, поэтому дальнейшие зависимости приведем для этого случая.

Принимаем, что a_ij, b_i, c_j подчинены нормальному закону распределения. В этом случае будет справедлива следующие детерминированные постановки:

и  _j — математическое ожидание и среднее квадратическое отклонение случайной величины c_j.

— соответственно, математические ожидания и дисперсии случайных величин a_ij и b_i;

— значение центрированной нормированной случайной величины в нормальном законе распределения, соответствующей заданному уровню вероятности соблюдения ограничений  _i.

Сделаем несколько замечаний к приведенным зависимостям:

• задача стохастического программирования сведена к задаче нелинейной оптимизации и может быть решена одним из рассматриваемых ранее методов;
• сравнение ограничения ресурса в стохастическом программировании и аналогичным ограничением в задаче линейного программирования показывает, что учет случайного характера величин a_ij и b_i приводит к уменьшению располагаемого ресурса на величину

т.е. к необходимости в дополнительном ресурсе. Однако этот дополнительный ресурс может оказаться неиспользованным, но для гарантированного выполнения плана его иметь необходимо.

В задачах принятия оптимальных решений широкое применение получил метод Монте-Карло. Основными особенностями этого метода, основанного на многократном повторении одного и того же алгоритма для каждой случайной реализации, являются: универсальность (метод не накладывает практически никаких ограничений на исследуемые параметры, на вид законов распределения); простота расчетного алгоритма; необходимость большого числа реализаций для достижения хорошей точности; возможность реализации на его основе процедуры поиска оптимальных параметров проектирования. Отметим основные факторы, определившие применение метода статистического моделирования в задачах исследования качества при проектировании: метод применим для задач, формализация которых другими методами затруднена или даже невозможна; возможно применение этого метода для машинного эксперимента над не созданной в натуре системы, когда натурный эксперимент затруднен, требует больших затрат времени и средств или вообще не допустим по другим соображениям.

1. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. – М.: Высшая школа, 1980. – 300 с.
2. Г о л ь ш т е й н Е. Г., Ю д и н Д. Б., Новые направления в линейном программировании, М., 1966; [2] Theorie der Hnearen parametrischen Optimierung, В., 1974.
3. «Математические методы: Учебник» / Партика Т.Л., Попов И.И. – М: ФОРУМ: ИНФРА, 2005.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986. –

Источник