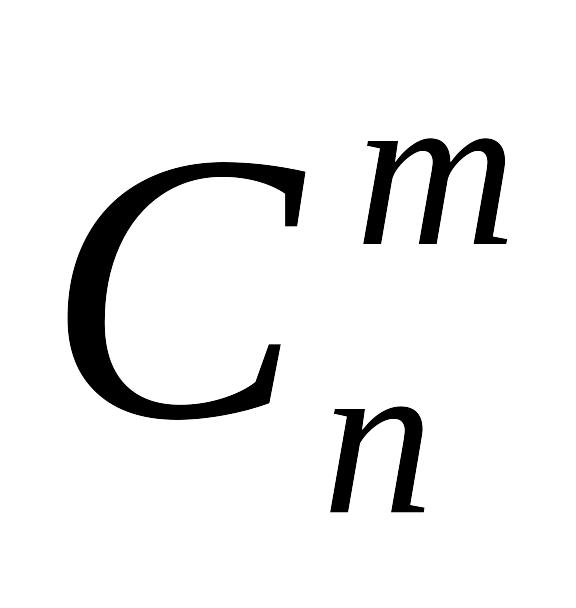Основные теоремы линейного программирования.
Определение: Множество точек называется выпуклым, если вместе с его любыми двумя точками ему принадлежит и весь отрезок, соединяющий их.
На рис. 33.1 изображено выпуклое множество (выпуклый многоугольник), а на рис. 33.2 — невыпуклое.
Утверждение: Пересечение конечного числа выпуклых множеств также выпуклое множество.
Определение: Точка выпуклого множества называется угловой (или крайней), если через неё нельзя провести ни одного отрезка, состоящего только из точек данного множества и для которого она была бы внутренней.
Для выпуклого многоугольника угловыми точками являются все его вершины. В пространстве выпуклое множество с конечным числом угловых точек называется выпуклым многогранником.
Утверждение: множеством решений системы m линейных неравенств с n переменными является выпуклый многогранник в n-мерном пространстве (исключая случай, когда система несовместна).
Как известно, любая задача линейного программирования может быть приведена к канонической модели минимизации линейной целевой функции с линейными ограничениями типа равенств. Поскольку число переменных в задаче линейного программирования больше числа ограничений (n > m), то можно получить решение, приравняв нулю (n — m) переменных, называемых свободными. Оставшиеся m переменных, называемых базисными, можно легко определить из системы ограничений-равенств обычными методами линейной алгебры. Если решение существует, то оно называется базисным. Если базисное решение допустимо, то оно называется базисным допустимым (опорным планом). Геометрически, базисные допустимые решения соответствуют вершинам (угловым точкам) выпуклого многогранника, который ограничивает множество допустимых решений. Если задача линейного программирования имеет оптимальные решения, то по крайней мере одно из них является базисным.
Приведенные соображения означают, что при поиске оптимального решения задачи линейного программирования достаточно ограничиться перебором базисных допустимых решений. Число базисных решений равно числу сочетаний из n переменных по m:
и может быть достаточно велико для их перечисления прямым перебором за реальное время. То, что не все базисные решения являются допустимыми, существо проблемы не меняет, так как чтобы оценить допустимость базисного решения, его необходимо получить. Такой путь решения задачи хотя и возможен, но весьма трудоемок, так как число допустимых базисных решений может быть весьма большим.
Теорема 33.1: Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.
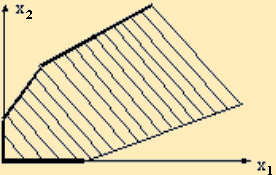
Ранее говорилось, что ограничениями любой задачи линейного программирования являются либо система линейных уравнений, либо система линейных неравенств. Совокупность решений таких систем при условии их совместности, образует выпуклые множества с конечным числом угловых точек. В частном случае, когда в систему ограничений — неравенств входят только две переменные и это множество можно изобразить на плоскости (рис. 33.2, 33.3).
Теорема 33.2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , где n — число неизвестных, а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.
Теорема 33.3: Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений системы ограничений, и наоборот.
Задача линейного программирования в стандартной форме с двумя переменными имеет вид:
Эти задачи допускают простое геометрическое истолкование. Рассмотрим вначале геометрическое истолкование системы ограничений задачи. Каждую совокупность значений переменных x1, x2 можно изобразить точкой на плоскости, если ввести систему координат и по одной оси откладывать x1, а по другой x2. Выясним, что геометрически означает совокупность решений одного отдельно взятого неравенства:
Рассмотрим прямую на плоскости с уравнением:
Эта прямая делит плоскость на две полуплоскости, в одной из которых справедливо наше неравенство, а в другой — противоположное. Для того, чтобы проверить, какая из полуплоскостей состоит из решений нашего неравенства, следует взять точку из какой-либо полуплоскости и проверить, выполняется ли наше неравенство в этой точке. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. Для системы из нескольких таких неравенств точки, координаты которых удовлетворяют всем неравенствам одновременно, должны находиться во всех соответствующих полуплоскостях, т.е. принадлежать теоретико-множественному пересечению этих полуплоскостей. Множество точек на плоскости, удовлетворяющих системе ограничений, составляет, таким образом, некоторую выпуклую многоугольную область (область допустимых решений). Условия неотрицательности переменных x1 ≥ 0 и x2 ≥ 0 приводят к тому, что эта область находится в первой координатной четверти.
При решении двумерных задач линейного программирования возможны следующие ситуации (ОДР — область допустимых решений):
1. Основной случай — получающаяся область имеет вид ограниченного (замкнутого) выпуклого многоугольника (см. рис. 33.2).
2. Не основной случай — получается неограниченный (незамкнутый) выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 33.3
3. Наконец, возможен случай, когда неравенства противоречат друг другу, и допустимая область вообще пуста.
Двумерные задачи линейного программирования решаются графически. Для случая N=3 можно рассмотреть трехмерное пространство и целевая функция будет достигать своё оптимальное значение в одной из вершин многогранника.
В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более трех весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
Основные утверждения линейного программирования. Теорема об оптимальном решении З. Л. П. В выпуклом многограннике
Опр 1. Множество точек называется выпуклым, если вместе с его любыми двумя точками ему принадлежит и весь отрезок, соединяющий их. Примерами выпуклых множеств являются: сектор, круг, многогранная область, прямая, отрезок, полуплоскость
Опр 2. Пересечение конечного числа выпуклых множеств также выпуклое множество.
Опр 3. Точка множества называется угловой или крайней, если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.
Опр4. Точка множества называется внутренней, если в некоторой ее окрестности содержатся точки только данного множества.
Опр5. Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.
Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника), а для невыпуклого множества — это не обязательно.
Опр6. Множество точек называется замкнутым, если оно включает все свои граничные точки.
Опр7. Множество точек называется ограниченным, если существует шар (круг) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.
Опр8. Выпуклое, замкнутое множество точек пространства (плоскости), имеющее конечное число угловых точек называется выпуклым многогранником если оно ограниченное, и выпуклой многогранной областью, если нет.
Множество всех допустимых решений совместной системы m линейных уравнений с n переменными (m Утв 1. Множеством решений системы m линейных неравенств с n переменными является выпуклый многогранник в n-мерном пространстве (исключая случай, когда система несовместна). Теорема. Если задача линейного программирования имеет оптимальное решение, то целевая функция принимает max (min) значение в одной из угловых точек многогранника решений. Если целевая функция принимает max (min) значение более чем в одной угловой точке, то она достигает его в любой точке, являющейся выпуклой линейной комбинацией этих точек. Вырождение, зацикливание,неразрешимость задач линейного программирования Вырождение — если некоторые из свободных членов=0, то в соответствующем опорном решение некоторые из базисных переменных окажутся 0. Если нулевой свободный член окажется в разрешающей строке, то Z не изменится после выполнения итерации. Тоже самое может быть и на 2,3 шаге. Теоретически не исключается возможность после нескольких шагов прийти к первоначальному опорному решению. Такая ситуация называется Зацикливание Если после очередной итерации окажется Bs0 то задача неразрешима и з-за несовместимости системы ограничений. Теорема о выборе разрешающего элемента при решении симплексным методом основной злп в случае неотрицательности свободных членов. Для того, что бы свободные члены системы ограничетельных уравнений остались неотрицательными, а значение целевой функции не уменьшилось при выполнении шага МЖИ достаточно 1 выбрать разрешающий столбец содержащий любую отрицательную оценку и хотя бы 1 положительный элемент(на практике выбирают максимум по модулю отриц. Оценку) 2 выбрать разрешающей ту строку, для которой отношение члена к положительному элементу разрешающего столбца минимум из всех таких отношений. Условие оптимальности и неразрешимости в случае неограниченности целевой функции для основной задачи линейного программирования в случае неотрицательности свободных членов.