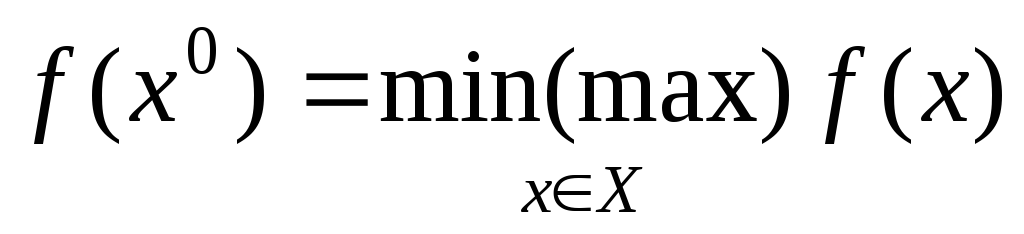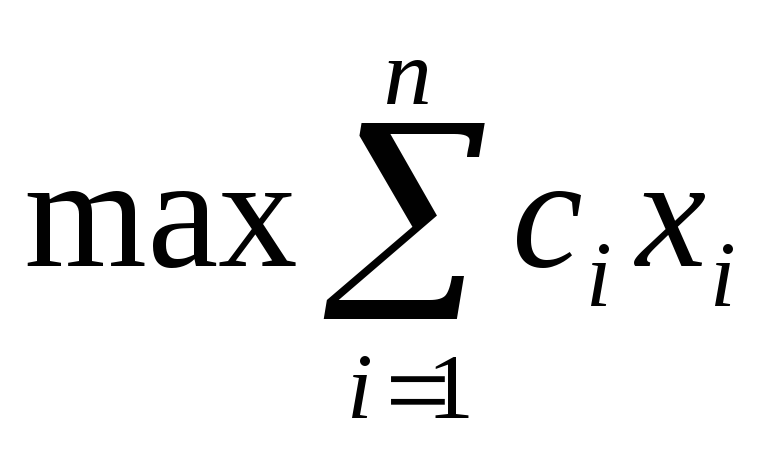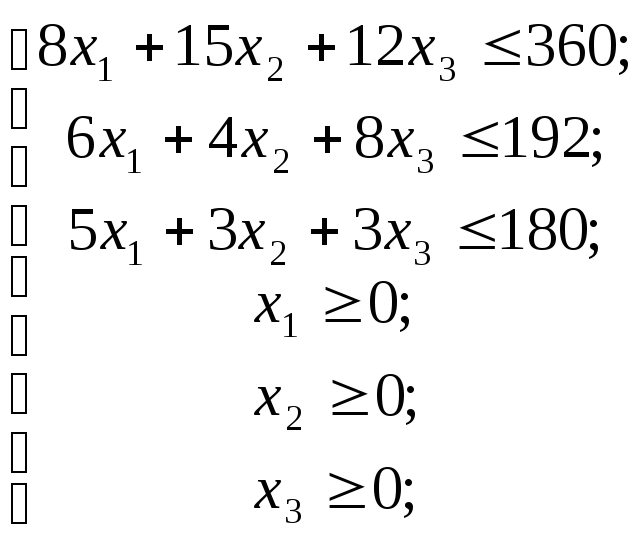Основные понятия линейного программирования кратко

МОТС / Часть2 / 15. Линейное программирование

На протяжении всей своей эволюции человек, совершая те или иные деяния, стремился вести себя таким образом, чтобы результат, достигаемый как следствие некоторого поступка, оказался в определенном смысле наилучшим. Двигаясь из одного пункта в другой, он стремился найти кратчайший среди возможных путь. Строя жилище, он искал такую его геометрию, которая при наименьшем расходе топлива, обеспечивала приемлемо комфортные условия существования. Занимаясь строительством кораблей, он пытался придать им такую форму, при которой вода оказывала бы наименьшее сопротивление. Можно легко продолжить перечень подобных примеров.

Наилучшие в определенном смысле решения задач принято называть оптимальными. Без использования принципов оптимизации в настоящее время не решается ни одна более или менее сложная проблема. При постановке и решении задач оптимизации возникают два вопроса: что и как оптимизировать?

Ответ на первый вопрос получается как результат глубокого изучения проблемы, которую предстоит решить. Выявляется тот параметр, который определяет степень совершенства решения возникшей проблемы. Этот параметр обычно называют целевой функцией или критерием качества. Далее устанавливается совокупность величин, которые определяют целевую функцию. Наконец, формулируются все ограничения, которые должны учитываться при решении задачи. После этого строится математическая модель, заключающаяся в установлении аналитической зависимости целевой функции от всех аргументов и аналитической формулировки сопутствующих задаче ограничений. Далее приступают к поиску ответа на второй вопрос.

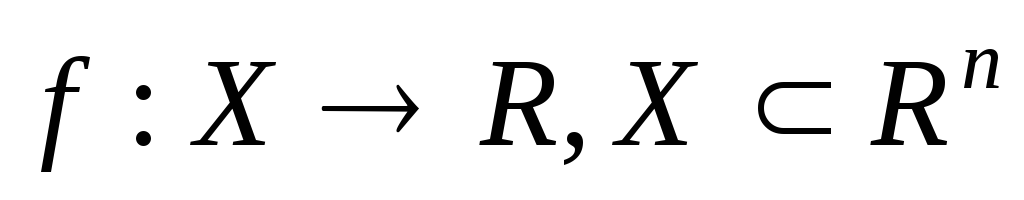
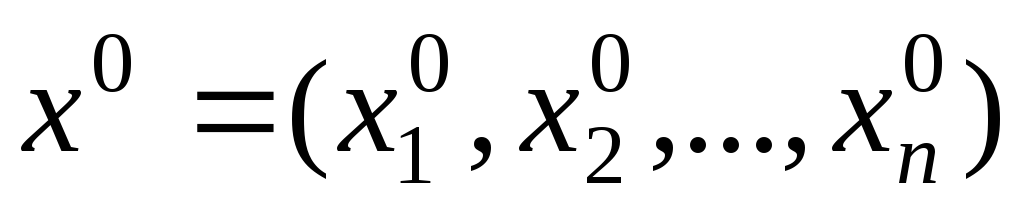
Итак, пусть в результате формализации прикладной задачи установлено, что целевая функция , где множество Х – обобщение ограничений, его называют множеством допустимых решений. Существо проблемы оптимизации заключается в поиске на множестве Х – множестве допустимых решений такого решения , при котором целевая функция f достигает наименьшего или наибольшего значения.

Составной частью методов оптимизации является линейное программирование.

15.2. Основные понятия линейного программирования

Первое упоминание (1938 г.) о математических методах в эффективном управлении производством принадлежит советскому математику Л. В. Канторовичу. Год спустя,в 1939 г., Л. В. Канторович опубликовал работу «Математические методы организации и планирования производства» и практически применил полученные результаты. Термин «линейное программирование» ввели американские математики Дж. Данциг и Т. Купманс в конце 40-х годов. Дж. Данциг разработал математический аппарат симплексного метода решения задач линейного программирования (1951 г.). Симплексный метод находит применение для решения широкого круга задач линейного программирования и до настоящего времени является одним из основных методов.

Линейное программирование — это раздел математики, ориентированный на нахождение экстремума (максимума или минимума) в задачах, которые описываются линейными уравнениями. Причем линейными уравнениями описывается как сама целевая функция, так и входные параметры (переменные) условия ограничений на входные параметры. Необходимым условием задач линейного программирования является обязательное наличие ограничений на ресурсы (сырье, материалы, финансы, спрос произведенной продукции и т.д.). Другим важным условием решения задачи является выбор критерия останова алгоритма, т. е. целевая функция должна быть оптимальна в некотором смысле. Оптимальность целевой функции должна быть выражена количественно. Если целевая функция представлена одним или двумя уравнениями, то на практике такие задачи решаются достаточно легко. Критерий останова алгоритма (или критерий оптимальности) должен удовлетворять следующим требованиям:

1. быть единственным для данной задачи;
2. измеряться в единицах количества;
3. линейно зависеть от входных параметров.

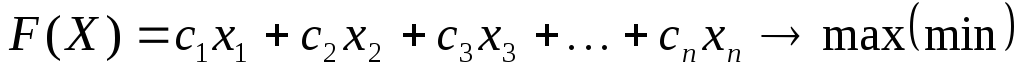
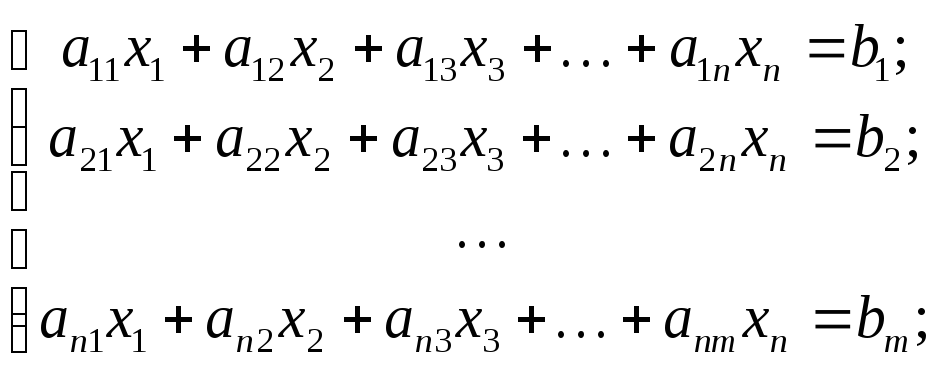
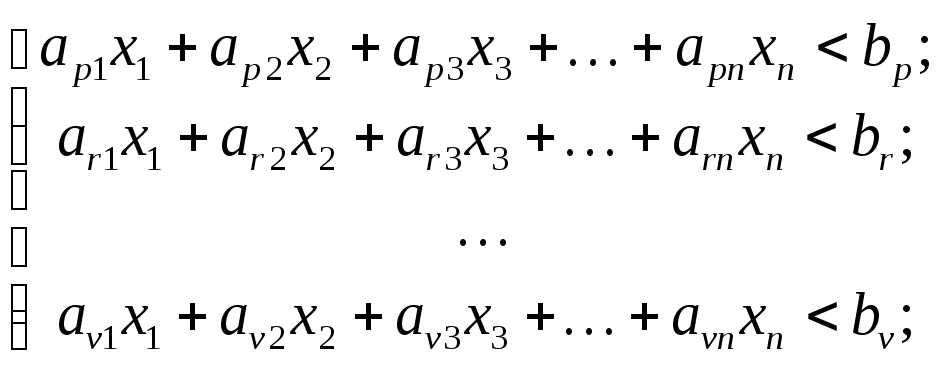
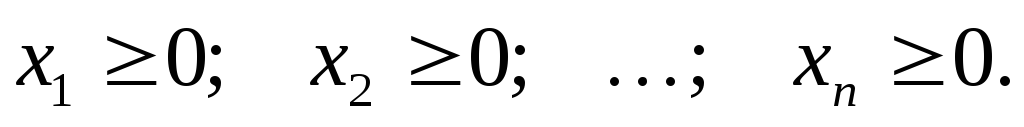
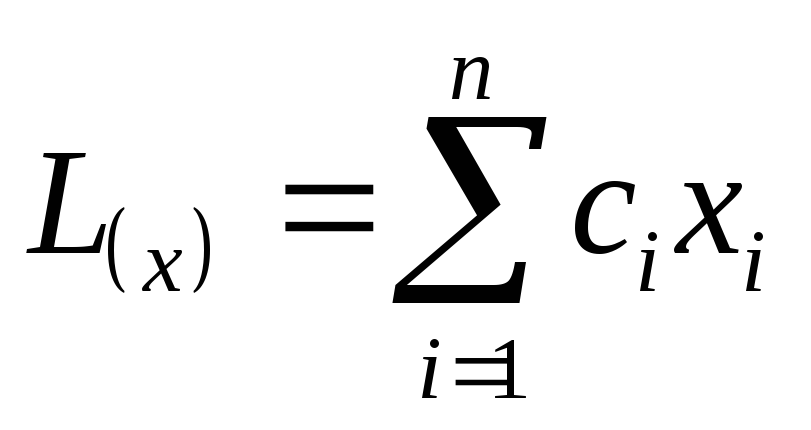
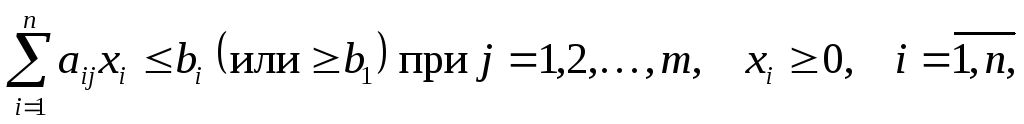
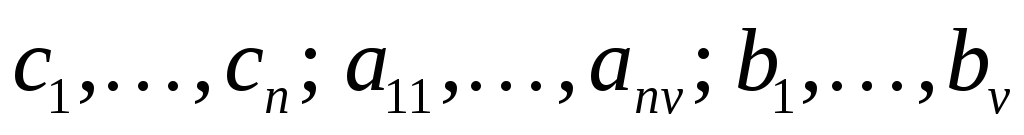
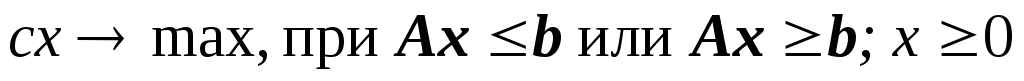
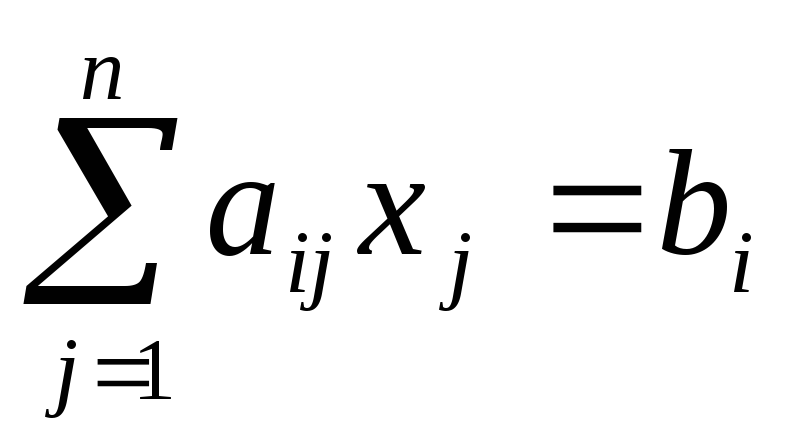
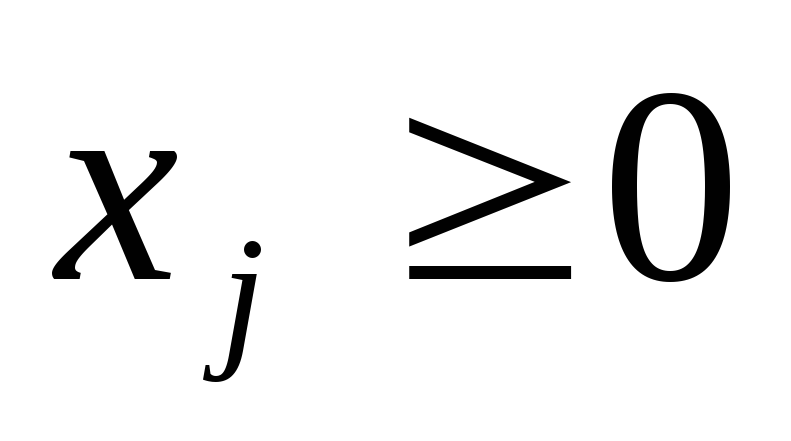
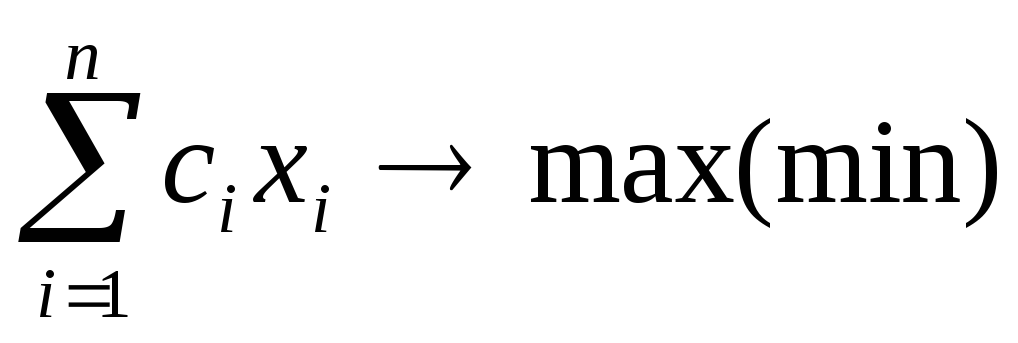
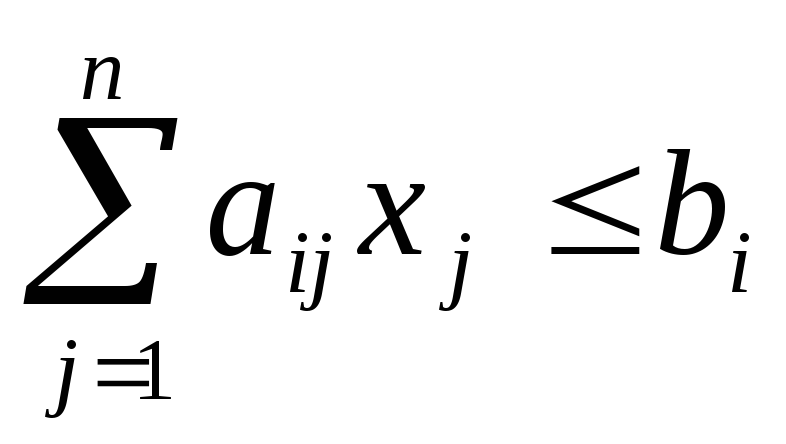
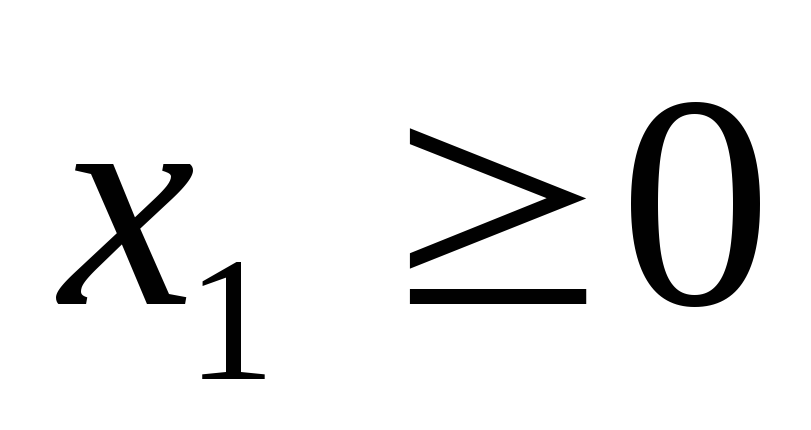
Исходя из вышесказанного, можно сформулировать задачу линейного программирования в общем виде: найти экстремум целевой функции (2.1) при ограничениях в виде равенств: (2.2) при ограничениях в виде неравенств: (2.3) и условиях неотрицательности входных параметров: (2.4) В краткой форме задача линейного программирования может быть записана так: (2.5) при условии (2.6) где — входные переменные; — числа положительные, отрицательные и равные нулю. В матричной форме эта задача может быть записана так: (2.7) Задачи линейного программирования можно решить аналитически и графически. 15.3. Каноническая задача линейного программирования, i=1,…,m,, j=1,…,n. Основные вычислительные методы решения задач линейного программирования разработаны именно для канонической задачи. 15.4. Общая задача линейного программирования Необходимо максимизировать (минимизировать) линейную функцию от n переменных. при ограничениях , i=1,…,k,, i=1+k,…,m,, …, Здесь k≤m,r≤n. Стандартная задача получается как частный случай общей при k=m,r=n; каноническая – при k=0,r=n. Пример. Кондитерская фабрика производит несколько сортов конфет. Назовем их условно «A», «B» и «C». Известно, что реализация десяти килограмм конфет «А» дает прибыль 90 рублей, «В» — 100 рублей и «С» — 160 рублей. Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограмм необходимо произвести, чтобы общая прибыль от реализации была максимальной. Нормы расхода сырья на производство 10 кг конфет каждого вида приведены в таблице 1. Таблица 1. Нормы расходов сырья на производство

Сырье	Нормы расхода сырья			Запас сырья
	А	В	С
Какао	18	15	12	360
Сахар	6	4	8	192
Наполнитель	5	3	3	180
Прибыль	90	100	160	максимум
Объем выпуска	Х1	Х2	Х3

Экономико-математическая формулировка задачи имеет вид Найти такие значения переменных Х=(х1, х2, х3), чтобы целевая функция 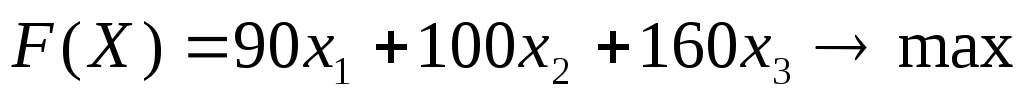при условиях-ограничениях:

Источник

Лекция 3. Линейное программирование

3.1. Линейное программирование как инструмент математического моделирования экономики

Линейное программирование сформировалось как отдельный раздел прикладной математики в 40 – 50-х гг. ХХ в. благодаря работам советского ученого, лауреата Нобелевской премии Л.В. Канторовича. В 1939 году им была опубликована работа «Математические методы организации и планирования производства», в которой он с использованием математики решил экономические задачи о наилучшей загрузке машин, раскрое материалов с наименьшими расходами, распределении грузов по нескольким видам транспорта и другие, предложив метод разрешающих множителей 8 .

Л.В. Канторович впервые сформулировал такие широко используемые экономико-математические понятия, как оптимальный план, оптимальное распределение ресурсов, объективно обусловленные оценки, указав многочисленные области экономики, где они могут быть применены.

Понятие линейного программирования было введено американским математиком Д. Данцигом, который в 1949 г. предложил алгоритм решения задачи линейного программирования, получивший название «симплексный метод».

Математическое программирование, в которое входит линейное программирование, в настоящее время является одним из направлений исследования операций. В зависимости от вида решаемых задач в нем выделяют такие области, как линейное, нелинейное, дискретное, динамическое программирование и др. Термин «программирование» введен в связи с тем, что неизвестные переменные, которые находятся в процессе решения задачи, обычно определяют программу или план работы некоторого экономического объекта.

В классическом математическом анализе исследуются общая постановка задачи определения условного экстремума. Однако в связи с развитием промышленного производства, транспорта, агропромышленного комплекса, банковского сектора традиционных результатов математического анализа оказалось недостаточно. Потребности практики и развитие вычислительной техники привели к необходимости определения оптимальных решений при анализе сложных экономических систем.

Главным инструментом для решения таких задач является математическое моделирование. При этом сначала строится простая модель, затем проводится ее исследование, позволяющее понять, какие из интегрирующих свойств объекта не улавливаются формальной схемой, после чего за счет усложнения модели обеспечивается большая ее адекватность реальности. Во многих случаях первым приближением к действительности является модель, в которой все зависимости между переменными, характеризующими состояние объекта, являются линейными. Практика показывает, что достаточное количество экономических процессов достаточно полно описывается линейными моделями. Следовательно, линейное программирование как аппарат, позволяющий отыскивать условный экстремум на множестве, заданном линейными уравнениями и неравенствами, играет важную роль при анализе этих процессов.

Линейное программирование получило широкое развитие в связи с тем, что было установлено: ряд задач сферы планирования и управления может быть сформулирован в виде задач линейного программирования, для решения которых имеются эффективные методы. По оценкам специалистов примерно 80–85 % всех решаемых на практике задач оптимизации относится к задачам линейного программирования.

Созданный математический аппарат в сочетании с компьютерными программами, производящими трудоемкие расчеты, позволяет широко использовать модели линейного программирования в экономической науке и практике.

Определение 1 9 .Линейное программирование (ЛП) – это область математического программирования, являющегося разделом математики и изучающего методы поиска экстремальных (наибольших и наименьших) значений линейной функции конечного числа переменных, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые представляют количественные соотношения между переменными, выражающие условия и требования экономической задачи и математически записываются в виде уравнений или неравенств, называются системой ограничений.

К задачам линейного программирования сводится широкий круг вопросов планирования экономических процессов, где ставится задача поиска наилучшего (оптимального) решения.

Общая задача линейного программирования (ЗЛП) состоит в нахождении экстремального значения (максимума или минимума) линейной функции, называемой целевой 10 :

(3.1)

от n переменных x₁, x₂, …, х_n при наложенных функциональных ограничениях:

(3.2)

и прямых ограничениях (требовании неотрицательности переменных)

, (3.3)

где a_ij, b_i, c_j – заданные постоянные величины.

В системе ограничений (3.2) знаки «меньше или равно», «равно», «больше или равно» могут встречаться одновременно.

ЗЛП в более краткой записи имеет вид:

,

;

.

Вектор Х = (x₁, x₂, …, х_n) компоненты которого удовлетворяют функциональным и прямым ограничениям задачи называют планом (или допустимым решением) ЗЛП.

Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений (ОДР). Допустимое решение, которое доставляет максимум или минимум целевой функции f(X), называется оптимальным планом задачи и обозначается f(X * ), где Х * =(x₁ * , x₂ * , …, х_n * ).

Еще одна форма записи ЗЛП:

,

где f(X * ) есть максимальное (минимальное) значение f(С, х), взятое по всем решениям, входящим в множество возможных решений Х.

Определение 2 11 . Математическое выражение целевой функции и ее ограничений называются математической моделью экономической задачи.

Для составления математической модели необходимо:

2) составить целевую функцию исходя из цели задачи;

3) записать систему ограничений, учитывая имеющие в условии задачи показатели и их количественные закономерности.

Источник