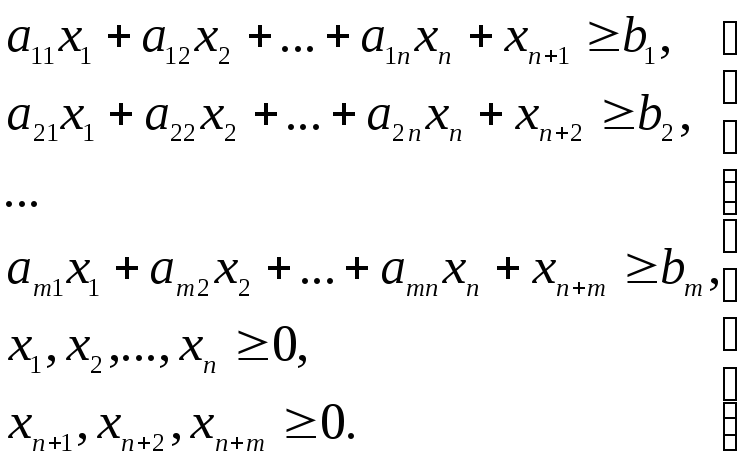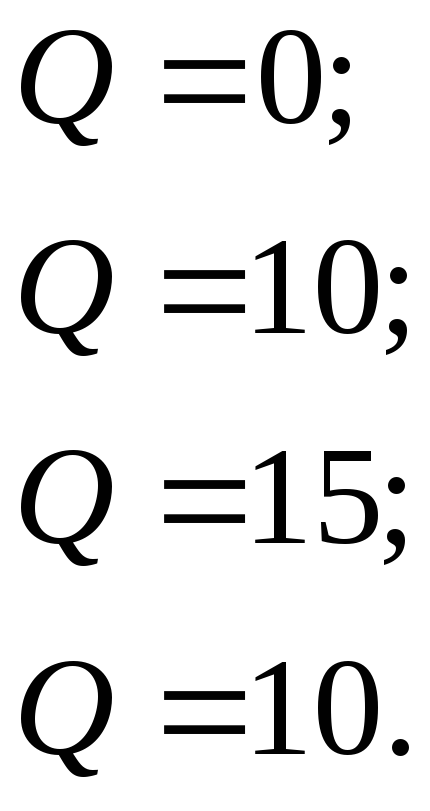Основные переменные прямой задачи линейного программирования

2. Линейное программирование

К задачам линейного программирования относятся такие оптимизационные задачи, в которых и целевая функция и ограничения – линейный многочлен.

2.1. Стандартный вид задачи линейного программирования (злп)

В стандартном виде ЗЛП целевая функция минимизируется, ограничения имеют вид равенств:

(2.1)

Здесь a_ij, b_i, p_i – постоянные коэффициенты.

В этих задачах количество переменных больше или равно количеству ограничений-равенств: n≥m.

Если n  m, то область допустимых решений – точка;

если n  m, то область допустимых решений – многогранник;

если n  m, то (m – n) ограничений линейно зависимы и их можно исключить.

2.2. Способы приведения задачи линейного программирования к стандартному виду

Случай 1. Исходные условия задачи: целевая функция минимизируется, ограничения представляют систему неравенств вида «меньше или равно».

Для приведения задачи к стандартному виду вводят искусственные переменные . Эти искусственные переменные прибавляют к левым частям ограничений:

(2.2)

Полученная задача тождественна исходной. Действительно, убрав искусственные переменные, получим левые части ограничений  b_i.

Случай 2. Исходные условия задачи: целевая функция минимизируется, ограничения имеют вид неравенств типа «больше или равно»:

Аналогично предыдущему случаю вводятся искусственные переменные, но эти переменные вычитаются из левых частей ограничений.

Случай 3. Исходные условия задачи: целевая функция максимизируется, ограничения имеют вид равенств.

Для приведения задачи к стандартному виду (2.1) сменим целевую функцию на целевую функциюG, все коэффициенты которой помножены на –1: Полученная задача тождественна исходной.

2.3. Графический метод решения задач линейного программирования

Графический метод применяется для решения задач небольшой размерности (количество переменных не превышает 3). Рассмотрим метод на примере решения следующей задачи:

(2.3)

1. Ограничения-неравенства заменяются на ограничения-равенст­ва:

1. Строятся графики полученных функций:

Рис. 2.1. Графический метод решения ЗЛП

1. Находится область допустимых решений (область, где выполняются все ограничения).
2. Строится график целевой функции при каком-либо значении правой части:

1. График целевой функции перемещается параллельно самому себе в сторону роста (уменьшения при Q  min) целевой функции до касания с границей области допустимых решений. Граничная точка (или отрезок прямой) является решением задачи линейного программирования.
2. Находится решение: координаты граничной точки (точка А) и значение целевой функции в этой точке:

Выводы: 1. Область допустимых решений задачи линейного программирования представляет собой выпуклый многогранник. 2. Решение задачи линейного программирования находится на границе области допустимых решений. Способ 2. Пункты 1–3 выполняются аналогично Способу 1.

1. Подсчитываются значения целевой функции во всех вершинах допустимого многогранника.

, следовательно, точка – решение задачи. Пример 1. Способ 1.

1. Ограничения-неравенства заменяются на ограничения-равенства:

1. Строятся графики полученных функций:

Рис. 2.2. 3. Находится область допустимых решений (область, где выполняются все ограничения). 4. Строится график целевой функции при каком-либо значении правой части: 5. График целевой функции перемещается параллельно его начальному положению в сторону уменьшения целевой функции до касания с границей области допустимых решений. Отрезок прямой АВ является решением задачи линейного программирования. 6. В ответе записываются функция, граничные точки отрезка и значение целевой функции на этом отрезке: , , Способ 2. 1 – 3 пункты выполняются аналогично Способу 1.

1. Подсчитываются значения целевой функции во всех вершинах допустимого многогранника.

–в двух точках, следовательно, отрезок AB, соединяющий эти точки, является решением задачи.

Источник