Основные переменные двойственной задачи линейного программирования

Двойственные задачи линейного программирования

Двойственная задача — это вспомогательная задача ЛП, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой, задачи. Приведем обобщенную формулировку двойственной задачи ЛП, которая применима к любой форме представления прямой задачи(приводимая ниже формулировка двойственной задачи является обобщенной в том смысле, что она применима ко всем формам прямой задачи).

Для математической задачи: всегда можно построить двойственную задачу вида:

Правила составления двойственной задачи по отношению к исходной:

1)число переменных двойственной задачи=числу ограничений прямой задачи;

2)коэф-тами к целевой функции дв.задачи яявляются правые части ограничений прямой задачи;

3)если исходная задача на max то двойственная на min;

4)матрица коэф-тов системы ограничений дв.задачи получается путем транспонирования матрицы коэф-тов системы ограничений прямой задачи;

5)если ограничения исх.задачи имеют ограничения = и наоборот;

6)правыми частями ограничений дв.задачи явл-ся коэф-ты цел.функции прямой задачи;

7)условия неотрицательности в обоих задачах сохраняются.

2. Экономическая интерпретация двойственной задачи

Пусть имеется задача о наилучшем использовании рес-ов:

(1) … … … aij – кол-во ресурсов iго типа на производства продукта j

Пусть У_i – цена 1 единицы i вида ресурса. Тогда за все рес-сы фирма заплатит:

Ограничения на знак в дв.задаче будут иметь только те переменные, которые имеют ограничения типа нер-ва.

Двойственная оценка показывает насколько увеличится значение целевой функции, если значение соотв-го рес-са увеличить на 1 единицу.

3 . Основное неравенство двойственности

Для любых допустимых планов прямой и двойственной задачи ЛП справедливо неравенство:

Доказательство: из дв.задачи (2)

Для любого допустимого плана пр-ва Х и любого доп-го вектора оценок У (с₁х₁+…+ с_nх_n) общая стоимость произведенной продукции не превосходит суммарной оценки рес-сов (b₁y₁+…+ b_my_m) .

1. Критерий оптимальности Канторовича.Если для некоторых допустимых планов х* и у* пары двойственных задач (1)и(2) выполняется равенство f(x)=g(y): C₁X₁+… +C_NX_N= b₁y₁+…+ b_my_m, то х* и у* являются оптимальными планами соответствующих задач.Док-во. Согласно основному неравенству двойственности, для любого допустимого плана х* прямой задачи и допустимого плана у двойственной справедливо неравенство g(y) < f(x*). Но по условию g(y*) = f(x*). Отсюда в силу транзитности отношений < и =, получим g(y)< g(y*). Так как у – произвольный план, то g(y*) есть максимальное значение целевой функции, то есть у – оптимальный план двойственной задачи. Аналогично доказывается, что х* является оптимальным для прямой задачи.

2.Основная теорема дв-ти:Если одна из задач двойственной пары имеет оптимальное решение, то и другая имеет оптимальное решение. Если же 1 из дв-ных задач не имеет решений на мн-ве доп.планов вследствии неограниченности целевой функции, то и 2 не имеет решения в силу пустоты мн-ва доп.планов. Т.е. если прямая задача имеет опт.решение, то дв-ная к ней также имеет опт.решение. Причем значение цел.функции на опт.планах прямой и дв-ной задач совпадают: F(X * )=G(Y * )

Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов.

3.Теорема о дополняющей нежесткости:

Для того чтобы X * =( X₁ * , .. X_n * ) и У * =( У₁ * , .. У_n * ) являлись оптим. планами прямой и двойственной задач, необх-мо и дост-но, чтобы выполнялись след.соотношения:

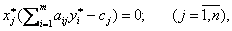
Экономически это означает, что если по некоторому оптимальному планупроизводства расход i -го ресурса строго меньше его запаса, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его i -я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку.

Источник

Решение двойственной задачи линейного программирования

Инструкция . Выберите количество переменных и количество ограничений прямой задачи линейного программирования, нажмите Далее . Полученное решение сохраняется в файле Word и Excel . При этом ограничения типа x_i ≥ 0 не учитывайте. Если прямая задача ЛП не имеет решение, но требуется составить двойственную задачу или одна из переменных x_i неопределена, то можно использовать этот калькулятор.

Определив обратную матрицу А -1 через алгебраические дополнения, получим:
Как видно из последнего плана симплексной таблицы, обратная матрица A -1 расположена в столбцах дополнительных переменных x₄ , x₅ , x₆ .
Тогда Y = C*A -1 =
Оптимальный план двойственной задачи равен: y₁ = 23.75, y₂ = 12.5, y₃ = 0
Z(Y) = 1100*23.75+120*12.5+8000*0 = 27625
Подставим оптимальный план прямой задачи в систему ограниченной математической модели:
0.1*250 + 0.2*5375 + 0.4*0 = 1100 = 1100
0.05*250 + 0.02*5375 + 0.02*0 = 120 = 120
3*250 + 1*5375 + 2*0 = 6125 < 8000 1-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₁>0).
2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₂>0).
3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y₃ = 0.
Таким образом, отличную от нуля двойственные оценки имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов.
При постановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим:
0.1*23.75 + 0.05*12.5 + 3*0 = 3 = 3
0.2*23.75 + 0.02*12.5 + 1*0 = 5 = 5
0.4*23.75 + 0.02*12.5 + 2*0 = 9.75 > 4
1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 1-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₁>0).
2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₂>0).
3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида использовать экономически не выгодно. И действительно в оптимальном плане прямой задачи x₃ = 0.
Величина двойственной оценки показывает, на сколько возрастает значение целевой функции при увеличении дефицитного ресурса на единицу.
Например, увеличении 1-го ресурса на 1 приведет к получению нового оптимального плана, в котором целевая функция возрастает на 23.75 и станет равной: F(x) = 27625 + 23.75 = 27648.75
Проведем анализ устойчивости оптимального плана и оценим степень влияния изменения ресурсов на значение целевой функции.
Пусть каждое значение параметра целевой функции изменится на ∆ с_i. Найдем интервалы, при которых будет экономически выгодно использование ресурсов.
1-ый параметр целевой функции может изменяться в пределах:

-3.8 ≤ с₁ ≤ 1
Таким образом, 1-параметр может быть уменьшен на 3.8 или увеличен на 1
Интервал изменения равен: [3-3.8; 3+1] = [-0.8;4]
Если значение c₁ будет лежать в данном интервале, то оптимальный план не изменится. 2-ый параметр целевой функции может изменяться в пределах:

-10 ≤ b₂ ≤ 30
Таким образом, 2-ый запас может быть уменьшен на 10 или увеличен на 30
Интервал изменения равен: [120-10; 120+30] = [110;150]
Составим субоптимальные варианты плана с учетом изменений исходных данных модели (таблицы).
Пусть 2-ый ресурс увеличили на 50

Базисные переменные	Значение базисных переменных	Коэффициент структурных сдвигов k c	Произведение k c на (50)	Расчет варианта плана
x 2	5375	6.25	312.5	5687.5
x 1	250	-2.5	-125	125
x 6	1875	1.25	62.5	1937.5
F(X)	27625	23.75	1187.5	28812.5

Пусть 1-ый ресурс уменьшили на -5

Базисные переменные	Значение базисных переменных	Коэффициент структурных сдвигов k c	Произведение k c на (-5)	Расчет варианта плана
x 2	5375	-12.5	62.5	5437.5
x 1	250	25	-125	125
x 6	1875	-62.5	312.5	2187.5
F(X)	27625	12.5	-62.5	27562.5

Задание : Для исходной задачи составить двойственную. Решить обе задачи симплексным методом или двойственным симплексным методом и по решению каждой из них найти решение другой. Одну из задач решить графическим методом.
F(X) = 3x₁ + x₂ → min
— 2x₁ + x₂≥4
2x₁ + x₂≤8
3x₁ + 2x₂≥6
Решение.
I этап. Приводим систему к каноническому виду.
II этап. Решаем симплекс-методом.
Примечание: Если задача решается данным калькулятором, то предыдущие два этапа пропускаем, поскольку они автоматически включены в решение.
На втором этапе окончательный вариант симплекс-таблицы имеет вид:

Базис	B	x₁	x₂	x₃	x₄	x₅	x₆	x₇
x₅	2	-7	0	-2	0	1	2	-1
x₄	4	4	0	1	1	0	-1	0
x₂	4	-2	1	-1	0	0	1	0
F(X3)	4	-5	0	-1	0	0	1-M	-M

Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым. Записываем оптимальный план:
x₁ = 0, x₂ = 4, F(X) = 1•4 = 4 Составим двойственную задачу к прямой задаче.
— 2y₁ + 2y₂ + 3y₃≤3
y₁ + y₂ + 2y₃≤1
4y₁ + 8y₂ + 6y₃ → max
y₁ ≥ 0, y₂ ≤ 0, y₃ ≥ 0
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи. Из теоремы двойственности следует, что Y = C*A -1 . Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

Источник

A = (A₅, A₄, A₂) =