7 Общая постановка задачи линейного программирования формы записи злп
Задача линейного программирования (ЗЛП) в общем виде имеет три формы:
произвольную, симметричную и каноническую.
1. Произвольная форма задачи ЛП имеет вид:
Выражение называется целевой функцией задачи. Величины (Х1,Х2,…,ХN) – переменные задачи. Система неравенств в задаче (2) определяет область допустимых значений (планов) задачи D, которая имеет форму выпуклого многогранника. Неравенства и равенства в задаче (2) называются ограничениями. Каждое неравенство определяет полупространство, а равенство – плоскость в пространстве переменных.
Решение задачи (2) называется оптимальным решением (или оптимальным планом) и обозначается как Х*=(Х*1,Х*2,…,Х*N).
Если область D ограничена, то задача ЛП всегда имеет либо единственное, либо бесконечно много решений. Если решение единственно, то оно совпадает с одной из вершин многогранника D. Если градиент целевой функции c=(с1,с2,…,сn) коллинеарен градиенту одного из ограничений, то задача имеет бесконечно много решений, лежащих на данном ограничении.
Если ограничения несовместны, или целевая функция неограниченна в неограниченной области D, то задача (2) не имеет решения. Всякая задача на минимум может быть сведена к задаче на максимум и наоборот, умножением целевой функции на –1. Оптимальный план задачи при этом не изменится, а значение целевой функции изменит знак. После решения надо снова изменить знак значения целевой функции.
2. Симметричная форма ЗЛП имеет два вида.
Симметричная форма задачи на максимум:
Задача (3) обычно имеет следующий экономический смысл: это объемы производства го вида продукции, цены или прибыль на единицу продукции, затраты го вида ресурса на производство го вида продукции, имеющийся запас го вида ресурса. Задача (3) ставится на определение такого плана производства продукции, который дает максимальную выручку или прибыль, при заданных ограничениях на имеющиеся ресурсы.
3. Каноническая форма задачи ЛП.
Определение. Если в ограничениях (5) есть переменные, отсутствующие в других ограничениях и с коэффициентами равными единице, то они называются базисными, остальные переменные называются свободными.
Каноническая форма с базисными переменными является исходной для решения задачи симплекс алгоритмом.
Для изготовления р1 ир2, используется ресурсы S1, S2. Запасы ресурсов число единиц затраченных на изготовление единицы продукции
Количество единиц затраченных на изготовление единицы продукции
Глава 1. Линейное программирование
Методы линейного программирования используются для широкого круга задач в естественных и гуманитарных науках, а также в хозяйственной деятельности. Так, например, математическое моделирование производственных процессов применяются при формировании плана производства, обеспечивающего максимизацию прибыли при заданных ограничениях на ресурсы.
Математически задача линейного программирования (ЗЛП) заключается в нахождении наибольшего или наименьшего значения линейной функции многих переменных при линейных ограничениях типа равенств и неравенств, когда на переменные есть или нет ограничений на знак.
В общем случае математическая постановка задачи линейного программирования может быть записана в виде:
(1)
(2) 
(3) 

(4) 

Здесь 


Целевая функция 
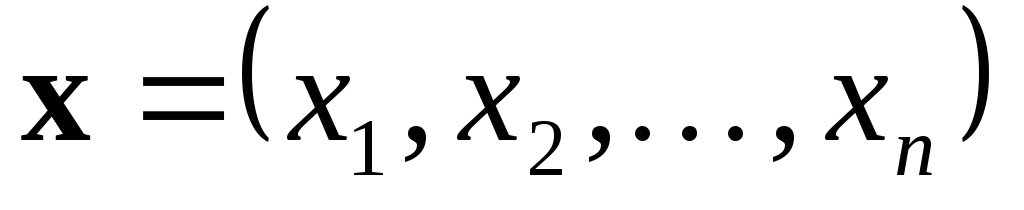
Аналогично можно записать задачу минимизации целевой функции. В этом случае целью является обычно минимизации затрат.
Условия (2) могут выражать ограниченность ресурсов. Например, затраты материалов, труда и времени, необходимые для реализации плана производства, не должны превышать имеющиеся запасы. Ограничения могут также отражать спрос на продукцию. Так в задачах о диете и суточном рационе, условия (2), задают необходимый минимум потребности в ингредиентах (витаминах, кормовых единицах и т.п.).
Переменные называют управляемыми. На эти переменные обычно накладывают условия неотрицательности (4), что соответствует их экономическому смыслу. Допустимо и наличие свободных переменных, на которые не накладываются условия на знак.
Решением задачи линейного программирования являются оптимальные значения управляемых переменных, которые обеспечивают максимум или минимум целевой функции.
Любой упорядоченный набор чисел 


План, удовлетворяющий всем ограничениям ЗЛП, называется допустимым планом.
В случае задачи максимизации (минимизации) допустимый план, доставляющий максимум (минимум) целевой функции, называется оптимальным планом.
Так как любое ограничение в виде равенства может быть приведено к ограничению в виде неравенства, а любое ограничение в виде неравенства может быть приведено к ограничению в виде равенства путем введения новых фиктивных переменных, исходная ЗЛП может быть записана в одном из специальных видов, стандартном или каноническом.
При записи в стандартном виде, ограничения формулируются в виде неравенств. Стандартный вид задачи максимизации:

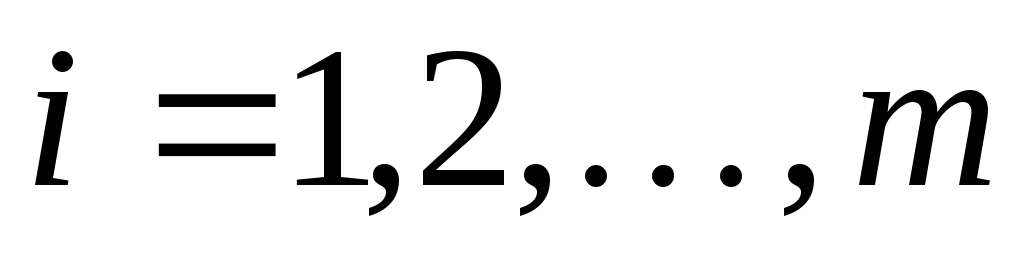


Обратите внимание на знак неравенств в ограничениях.
Стандартный вид задачи минимизации:

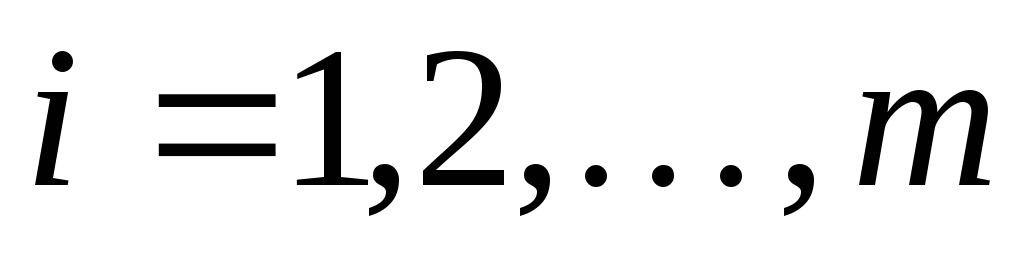
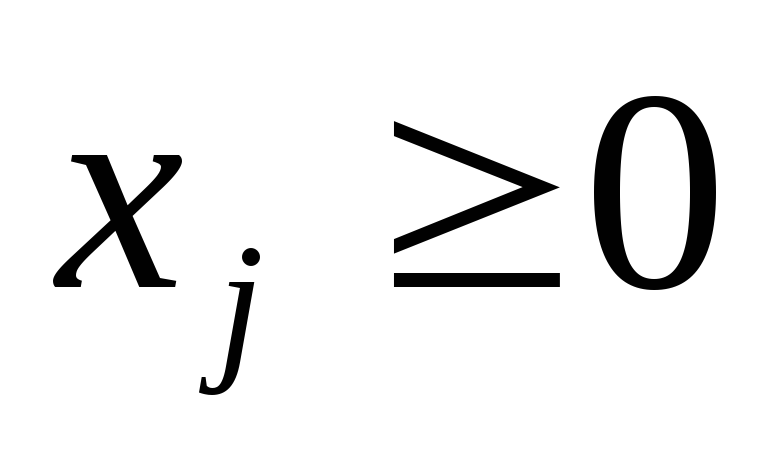

При записи в каноническом (или классическом) виде, ограничения формулируются в виде равенств.
Канонический вид задачи максимизации:

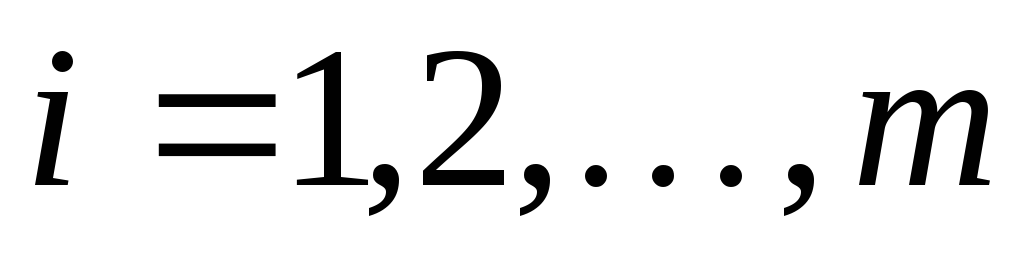


Канонический вид задачи минимизации:




ЗЛП можно записывать в матричном виде.
Стандартная задача максимизации в матричном виде:


Стандартная задача минимизации в матричном виде:

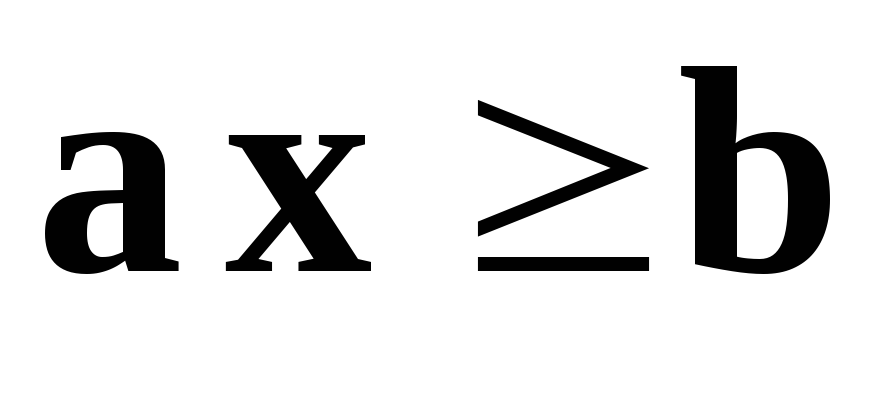

,
(1.8)
Иногда используют другую форму записи ограничений, вводя обозначение для множества допустимых планов.
, (1.9)
Таким образом, задача линейного программирования (1.2) с использованием обозначения (1.9), заключается в нахождении неотрицательных значений управляемых переменных 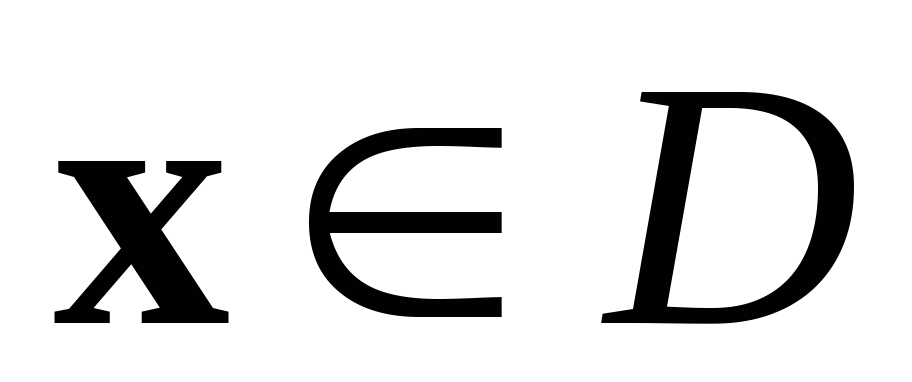

В силу того, что целевая функция линейна, а, следовательно, непрерывна, решение существует, если множество допустимых планов непустое и ограниченное.
При решении ЗЛП обычно нужно перейти от словесной формулировки к математическому описанию. Для этого нужно:
- Идентифицировать искомые переменные задачи, то есть указать перечень управляемых переменных
, набор которых описывает возможное решение.
- Задать ограничения, задающие множество допустимых планов, записать их в форме неравенств или уравнений относительно компонент плана.
- Сформулировать критерий для оценки альтернатив. То есть построить целевую функцию.
Задача А1.41. Для изготовления различных изделий А, В, С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в табл. 1.1. Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида. Составьте план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.
| Таблица 1.1 | ||||
| Видысырья | Нормы затрат сырьяна одно изделие | Общее количествосырья | ||
| А | В | С | ||
| I | 18 | 15 | 12 | 360 |
| II | 6 | 4 | 8 | 192 |
| III | 5 | 3 | 3 | 180 |
| Цена одногоизделия (руб.) | 9 | 10 | 16 | |
Построим математическую модель задачи. 1). Укажем искомые переменные задачи: 
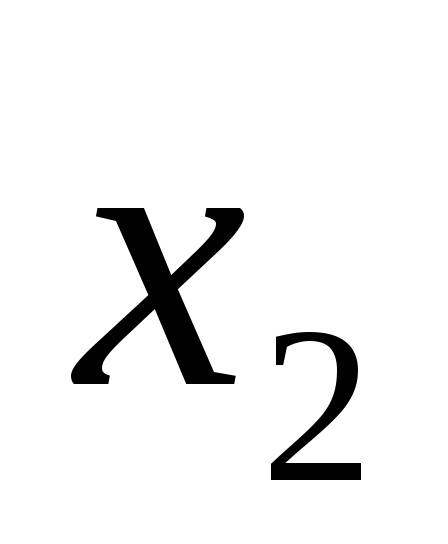


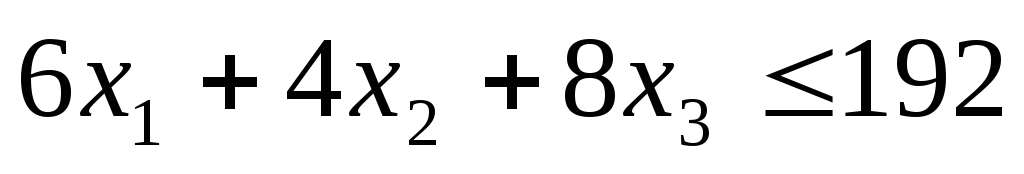






| Таблица 1.2. | |||||
| Питательныевещества | Продукты | ||||
| Хлеб | Соя | Сушеная рыба | Фрукты | Молоко | |
| Белки | 2 | 12 | 10 | 1 | 2 |
| Углеводы | 12 | 0 | 0 | 4 | 3 |
| Жиры | 1 | 8 | 3 | 0 | 4 |
| Витамины | 2 | 2 | 4 | 6 | 2 |
| Цена | 24 | 75 | 64 | 36 | 10 |
Построим математическую модель задачи. 1). Искомые переменные задачи – количество каждого из 5 ингредиентов, входящих в диету. 













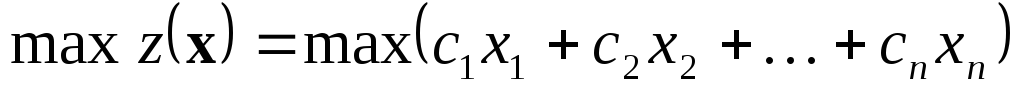







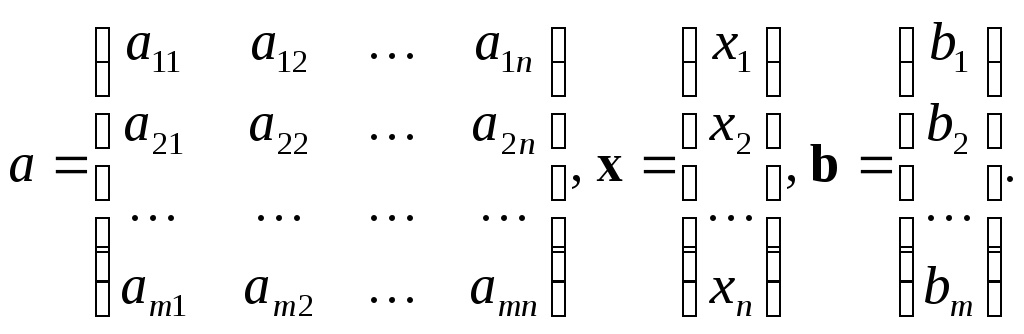


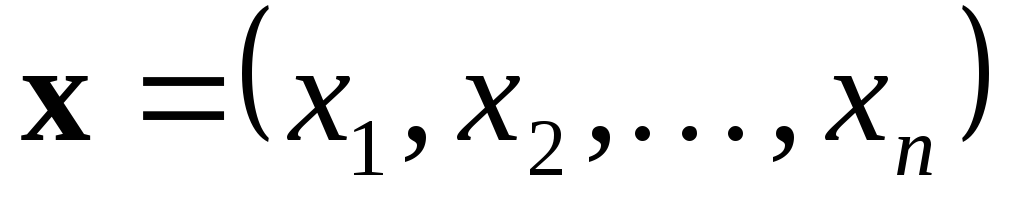 , набор которых описывает возможное решение.
, набор которых описывает возможное решение.