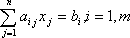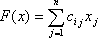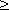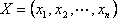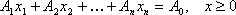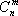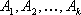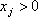Оптимальное решение задачи линейного программирования может быть достигнуто

22. Условие существования оптимального решения задачи линейного программирования

Теорема 1. Пусть исходная задача решается на максимум. Если для некоторого опорного плана все оценки _j неотрицательны, то такой план оптимален. Доказательство. Так как Z= ₀ — и по условию _j0 , то Z достигает максимального значения при =0. Это возможно лишь при x_m+1=0, x_m+2=0, . x_n=0, т. е. опорный план (b₁, b₂, . b_m, ) оптимален.

Теорема 2. Если исходная задача решается на минимум и для некоторого опорного плана все оценки _j неположительны, то такой план оптимален.

Доказательство аналогично предыдущему случаю.

Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным.

23. Метод прямого перебора решения злп

Метод прямого перебора – метод, когда перебирают угловые точки и подставляют в целевую функцию любое базисное решение системы линейных уравнений (координаты угловой точки). Из них выбираем минимальное.

Если известна функциональная связь целевой функции Y и искомой переменной X, то можно последовательно вычислить значения целевой функции для некоторых значений искомой переменной. Вычисления повторяются до тех пор, пока не будет найден min (max) значения целевой функции

Y=f(x₁, . x_i, . x_n, u₁, . u_j, . u_m),

x_i=x_0i+x_ik (k=0, 1, 2, . l).

Этот метод может быть использован для решения задач исследования операций, если имеются одна искомая переменная или несколько с небольшим диапазоном изменения искомых переменных.

Особенность и преимущества метода прямого перебора заключаются: 1) в независимости поиска от вида и характера целевой функции; 2) в цикличности поисковой процедуры; 3) в определении глобального экстремума целевой функции; 4) в простоте алгоритма и программы оптимизации; 5) в малом объеме необходимой машинной памяти.

В случае большой области изменения искомой переменной и (или) наличия более чем одного экстремума исследуемой функции использование этого метода неэффективно.

24. Основная идея симплекс-метода решения злп и ее теоретическое обоснование

Его суть в следующем. Если известны какая-нибудь крайняя точка и значение целевой функции, то все крайние точки, в которых целевая функция принимает худшее значение, заведмо не нужны. Отсюда естественно стремление найти способ перехода от данной крайней точки к смежной по ребру лучшей, от нее к еще лучшей (не худшей). Для этого нужно иметь признак того, что лучших крайних точек, чем данная крайняя точка, вообще нет. В этом и состоит общая идея наиболее широко применяемого симплексного метода ( метода последовательного улучшения плана) для решения ЗЛП. Итак, симплексный метод предполагает : 1) умение находить начальный опорный план; 2) наличие признака оптимальности опорного плана; 3) умение переходить к нехудшему опорному плану.

Теоретические обоснования симплекс-метода.

Любую ЗЛП можно представить в эквивалентном предпчтительном виде:

Выразим базисные переменные х₁, х₂, . x_m из равенств (2.59) через свободные х_m+1, х_m+2, . x_n и подставим их в целевую функцию. После группировки подобных членов получим

где с_б=(c₁, c₂, . c_m) — вектор коэффициентов целевой функции при базисных переменных; А₀=(b₁, b₂, . b_m) T — вектор-столбец свободных членов; А_j=(a_1j, a_2j, . a_mj) T — вектор-столбец коэффициентов при переменных х_j.

С учетом равенств (2.61)—(2.63) задача (2.58)—(2.60) примет вид:

Задачу (2.64)—(2.66) записывают в таблицу, которая называется симплексной (табл.1). Последнюю строку называют индексной строкой (строкой целевой функции), число ₀= с_бА₀ — значение целевой функции для начального опорного плана х₀, т.е. ₀=Z(х₀). Числа _j=с_бА_jc_j называются оценками свободных переменных.

Источник

Общая задача линейного программирования.

3) цель задачи ()

(max F(x))

(min F(x))

Определение: Планом или допустимым решением задачи линейного программирования называется вектор , удовлетворяющий условиям 1) и 2)

(*)

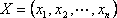
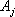
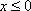
Определение: План называетсяопорным, если векторы , входящие в разложение (*) с положительными коэффициентами, являются линейно независимыми.

Определение: Опорный план называется невырожденным, если он содержит m – положительных компонентов, в противном случае опорный план называется вырожденным.

Определение: Оптимальным планом (решением) задачи линейного программирования называется план, доставляющий линейной форме наибольшее или наименьшее значение.

В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, либо система ограничений смешанная, однако любую систему ограничений можно привести к системе уравнений. Для этого достаточно к левой части каждого неравенства прибавить (для ) или отнять (для) какое-то неотрицательное число (добавочную переменную) с тем, чтобы каждое неравенство обратилось в уравнение, в результате получим эквивалентные системы уравнений и неравенств.

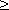
Основные теоремы линейного программирования

Теорема 1: Множество всех допустимых решений системы ограничений задачи линейного программирования, является выпуклым.

Теорема 2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , гдеn — число неизвестных , а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.

Теорема 3: Если известно, что система векторов в разложении линейно независима и такова, что, где, то точкаявляется угловой точкой многогранника решений.

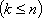
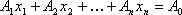
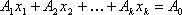
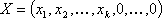
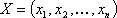
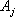
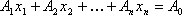
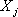
Теорема 4: Если — угловая точка многогранника решений, то векторыв разложении, соответствующие положительным, являются линейно независимыми.

Следствие 1: Так как векторы 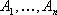имеют размерностьm, то угловая точка многогранника решений имеет не более m положительных компонент .

Следствие 2: Каждой угловой точке многогранника решений соответствует линейно независимых векторов системы векторов.

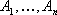
Симплексный метод решения задачи линейного программирования.

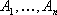
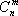
Доказано, что оптимальное решение задачи линейного программирования связано с угловыми точками многоугольника решений, то есть с опорными планами. Они определяются системой m — линейно независимых векторов, содержащихся в системе из n — векторов. Количество опорных планов меньше, гдеn — число неизвестных, а m – число ограничений. При больших n и m найти все их перебором очень трудно, поэтому необходимо упорядоченный перебор, такой схемой является симплексный метод, который позволяет исходя из известного опорного плана задачи, за конечное число шагов получить её оптимальный план. Каждый из шагов (итераций) состоит в нахождении нового плана, которому соответствует меньшее для задачи на минимум (большее для задачи на максимум) значение линейной формы, чем её значение в предыдущем плане. Процесс продолжается до получения оптимального плана. Если задача не обладает планами или её линейная форма неограниченна на многограннике решений, то симплексный метод позволяет установить это в процессе решения.

Источник

Возможные случаи допустимого множества решений задачи линейного программирования

Возможные случаи оптимальных решений (планов) задачи линейного программирования.

Графоаналитический способ решения задач линейного программирования

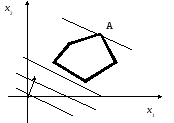
Графоаналитический (графический) способ решения задач линейного программирования обычно используется для решения задач с двумя переменными, когда ограничения выражены неравенствами, а также задач, которые могут быть сведены к таким задачам. Пусть задача линейного программирования имеет вид: 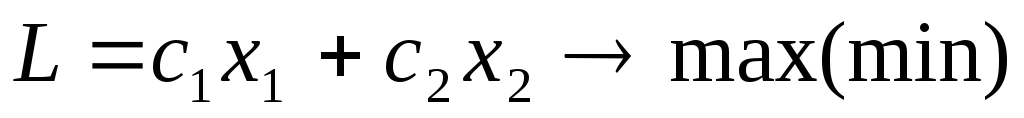(1.6) (1.7) где с₁, с₂, а_i1, а_i2, b_i — заданные действительные числа; знаки в неравенствах произвольны; целевая функция либо максимизируется, либо минимизируется. Каждое из неравенств (1.7) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми ;i=1,…,m. В том случае, если система неравенств (1.7) совместна, допустимая область решений задачи есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых значений является выпуклое множество, которое называютмногоугольникомрешений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки равенств. Множеством допустимых решений для данной частной задачи может быть:

• пустая область;
• выпуклый многоугольник, включая вырожденные случаи — отрезок и единственную точку;
• выпуклая многоугольная неограниченная область, включая вырожденные случаи — луч и прямую.

Практическая реализация решения задачи линейного программирования (1.6) – (1.7) на основе ее геометрической интерпретации включает следующие этапы: 1. Построить прямые, уравнения которых получаются в результате замены в ограничениях (1.7) знаков неравенств на знаки равенств. 2. Найти полуплоскости, определяемые каждым из ограничений. Соответствующая полуплоскость может быть найдена подстановкой в неравенство координат какой-нибудь «простой» точки — (0,0), (0,1) или (1,0). Главное — чтобы эта точка не принадлежала границе полуплоскости. Если после подстановки неравенство окажется справедливым, то выбирается та полуплоскость, где содержится эта точка. Если неравенство не справедлива, то выбирается альтернативная полуплоскость. 3. Определить многоугольник решений, как пересечение найденных полуплоскостей. 4. Построить градиент целевой функции, т.е. 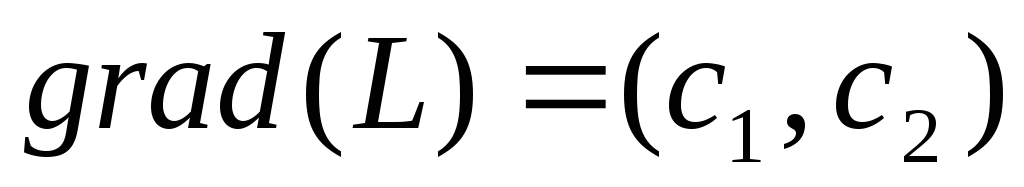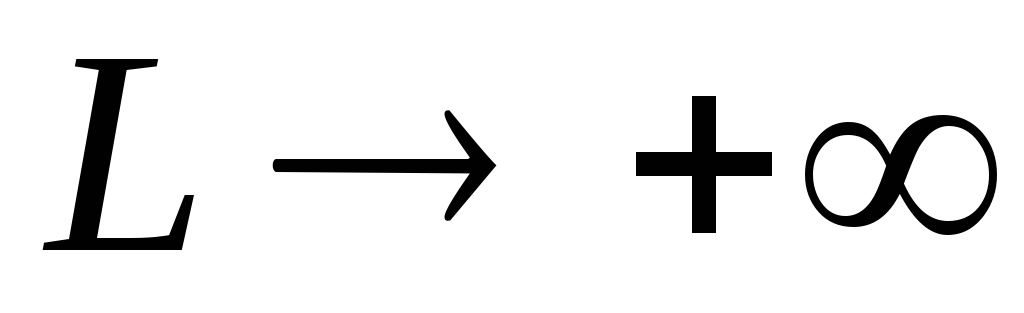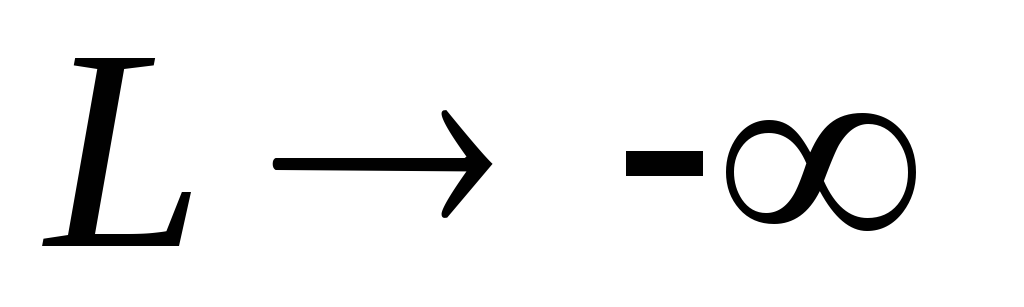вектор_, координатами которого служат коэффициенты целевой функцииL. Этот вектор определяет направление наискорейшего возрастания целевой функции. 5. Построить ряд линий уровня целевой функцииL, т.е. прямых перпендикулярных градиентуL. При этом построение линий уровня следует вести в направлении градиента, если решается задача на максимум, и в противоположном направлении (в направлении «антиградиента»), если решается задача на минимум. В результате отмечается точка (точки), в которой линии уровня в последний раз касаются допустимого множества. Если допустимое множество неограниченно, то точки последнего касания может и не быть. Линии уровня уходят в бесконечность, соответственно значение или, и задача не имеет оптимальных планов.

1. Определить координаты отмеченной точки аналитически, решая соответствующую систему линейных уравнений. Затем вычислить значение целевой функции в этой точке. Тем самым, определяется оптимальный план и оптимальное значение целевой функции задачи.

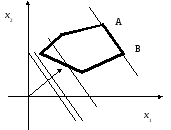
Заканчивая рассмотрение геометрической интерпретации задачи (1.6) – (1.7), отметим, что при нахождении ее решения могут встретиться случаи, изображенные на рис. 1.1 – 1.3. Рис. 1.1 характеризует такой случай, когда целевая функция принимает оптимальное значение в единственной точке А, одной из вершин допустимого множества. На рис. 1.2 оптимальное значение целевая функция принимает в любой точке отрезка АВ. На рис. 1.3 изображен случай, когда оптимальное значение целевой функции недостижимо. Рис. 1.1. Оптимум функции L достижим в точке А Рис. 1.2. Оптимум функцииLдостигается в любой точке отрезка АB Рис. 1.3. Оптимум функции Lнедостижим

Источник