Задачи дискретной оптимизации.
Развитие методов решения задач дискретной оптимизации обусловлено теоретической и практической важностью этих задач, встречающихся в различных областях науки и техники. Развитие методов идет в основном по пути создания новых численных методов для решения как общих задач дискретного программирования (оптимизации), так и задач частного вида. Существующие сейчас методы дискретного программирования по способу достижения оптимума можно разделить на три основных вида:
- методы отсечения;
- комбинаторные методы;
- приближенные методы.
На основе этих методов иногда разрабатываются гибридные методы. Интенсивное развитие получили комбинаторные методы. Это вызвано тем, что на практике необходимо решать большое количество оптимизационных, комбинаторных задач. Такими задачами, к примеру, являются:
- задача о ранце;
- задача о коммивояжере;
- задача минимизации среднего времени обработки партии деталей;
- задача о назначениях;
- задача о покрытии;
- задача компоновки;
и так далее. Определить понятие оптимизационно-комбинаторной задачи можно следующим образом: пусть имеется множество из n элементов. На этом множестве задается множество комбинаций 


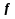
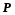

- нужно уметь перебирать множество значений функции
;
- вычислять эти значения и сравнивать.
Для решения оптимизационно-комбинаторных задач было разработано большое число алгоритмов, общая идея которых состоит в замене полного перебора всех вариантов частичными переборами меньших объемов. Для осуществления этого производится отбрасывание некоторых подмножеств, заведомо не содержащих искомого экстремума и сужении области перспективных вариантов. При этом получаются весьма разнообразные методы, определяемые структурой соответствующих конечных множеств 
- локальная оптимизация;
- случайный поиск;
- метод ветвления.
Рассмотрим кратко суть этих методов. При локальной оптимизации для каждой комбинации 



- признаки выбираются заранее путем анализа условий задачи;
- признаки получают из анализа уже полученных решений.
Методы ветвления. Впервые метод ветвей и границ был предложен для решения задач целочисленного линейного программирования. В дальнейшем этот метод был применен в более общим классам комбинаторных оптимизационных задач. По способу ветвления все алгоритмы ветвей и границ можно разделить на следующие группы:
- алгоритмы, строящие дерево подзадач исходной задачи(например, алгоритм Лэнд и Дойга, предложенный для решения задач целочисленного программирования. В этом методе строится дерево задач линейного программирования, добиваясь постепенного удовлетворения условий целочисленности);
- алгоритмы, строящие дерево недопустимых решений(например, аддитивный алгоритм Балаша и его модификации). Этот метод применяется для решения задач линейного программирования с булевыми переменными;
- алгоритмы, строящие дерево допустимых решений(например, метод решения задач о коммивояжере).
Общая схема метода ветвей и границ для задачи дискретной оптимизации


- подсчет оценок (ищется нижняя граница целевой функции
на множестве
). Нижней оценкой будет такое число
, что
;
- многошаговый процесс разбиения множества
на подмножества(ветвление по определенным правилам);
- пересчет оценок. Если множество
, то
. Если множество
состоит из объединения
, то есть
, то оценка для любого подмножества
будет не меньше, чем оценка для множества
, то есть:


- признак оптимальности(в том случае когда решаем задачу на минимум)
в случае, если 

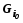

- вычислить оценку
. Если удается найти такоеx, что
, тоx — оптимальное решение. Если оптимальное решение не обнаружено, то по некоторому правилу разбиваем множество
на подмножества
;
- считаем оценки
множеств
. Если при этом удается найти такоеx, что
,
, тоx — оптимальное. Если такого x не обнаружили, то для дальнейшего разбиения выбираем множество
с минимальной оценкой. Разбиваем это множество на несколько подмножеств и повторяем процесс до тех пор, пока не получим оптимальное решение.
Для продолжения скачивания необходимо пройти капчу:
Методы решения задач дискретной оптимизации.
Задачи дискретной оптимизации – это задачи, в которых на варьируемые значения накладываются требования дискретности.
g(x)<(>.=)bj, xj принадлежит Dj – множеству допустимых значений параметра xj.
Классификация задач дискретной оптимизации: В зависимости от характера изменения параметров различают: полностью дискретные, частично-дискретные, целочисленные задачи и задачи с булевыми переменными.
1) Метод отсечений – предназначен для решения линейных целочисленных или частично целочисленных задач.
2) Комбинаторные методы 3) Приближенные методы
1) Метод отсечения. Решение задач целочисленной линейной оптимизации методом отсечений сводится к решению последовательности спец. образом построенных задач P0,P1,Ps. Задача P0 образуется из исходной задачи путем отбрасывания условия целочисленности. Каждая последующая задача P1,P2…Ps, образуется из предыдущей путем добавления к ней дополнительных линейных ограничений, которые называются правильным отсечением. Методы отсечения различаются между собой способами формирования дополнительных ограничений. Наиболее распространенным является метод отсечения Гомори.
Основные шаги метода ГОМОРИ.
1) Определение оптимального решения исходной задачи без учета требований целочисленности. Условие целочисленности отбрасывается и задача решается обычным симплекс- методом.
2) Если полученное решение целочисленное – то работа алгоритма заканчивается, в противном случае переход к шагу 3
3) На основании последней симплекс таблицы формируем отсечение ГОМОРИ. ∑xj >=, s номер строки таблицы, которой соответствует переменная с наибольшей дробной частью.
4) Добавление дополнительных ограничений к условию решаемой задачи: ∑xj -xd=, где xd- дополнительная переменная, умноженная на -1 — ∑xj +xd=-.Добавляется к последней симплекс таблице и полученная задача решается двойственным сиплекс методом.
Недостатки; метод может использоваться для решения частично- целочисленных задач. Недостатки: метод используется для решения линейно-целочисленных задач. В процессе решения при добавлении дополнительных ограничения размер задачи возрастает.
2) Комбинаторные методы. К ним относятся метод ветвей и границ, он используется как для решения линейных так и нелинейных задач. Основан на использовании конечности множества допустимых вариантов и замене полного перебора частичным перебором. Полного перебора удается избежать путем отбрасывания неперспективных множеств, т.е. множеств, где заранее нет перспективного решения. В процессе поиска строится дерево вариантов. Каждой подвершине дерева вариантов соответствует подзадача исходной задачи.
3) Приближённые методы. Для точного алг-ма нужно знать трудоёмкость и память. Для приближенного алгоритма, кроме трудоемкости и памяти, вводят такие параметры, как относительная погрешность еА алгоритма А и вероятность несрабатывания 6А алгоритма А.
Постановка задач нелинейного программирования. Задачи выпуклого программирования. Функция Лагранжа, принципы ее построения. Метод множителей Лагранжа для решения задач на условный экстремум.
1) В общем виде задача нелинейной оптимизации может быть сформулирована в следующем виде: f(x)->max (min);
gi(x)bi, i=1..m. При этом хотя бы одна из функций f(x) или gi(x) является нелинейной. Задача с ограничениями называется задачей с условной оптимизацией, а задачи без ограничений- задачи безусловной оптимизации.
Для задач безусловной оптимизации необходимое условие экстремума заключается в том, что в оптимальной точке все частные производные целевой функции должны быть равны 0. Для проверки достаточного условия экстремума необходимо построить матрицу вторых производных G(x*)целевой функции в оптимальной точке.
Характер точки X* связан со знакоопределенностью квадратичной формы: X T G(X*)X, x не равен 0.
Данная квадратичная форма является положительно определенной если она > 0, отрицательно определенной если она < 0, Положительно полуопреленная если она >=0, отрицательнополуопреленная
Если квадратичная форма в точке х* является положительноопределенной, то в этой точке функция имеет локальный минимум, если квадратичная форма является отрицательноопределенной, то в этой точке функция имеет локальный максимум. Если она является неопределенной, то функция не имеет экстремума в данной точке, если функция является полуопределенной, то требуетсядополнительное исследование.
Для проверки знакоопределенности используют критерий Сильвестра, согласно которому квадратичная форма положительноопределена тогда, когда все главные миноры матрицы G(x*) положительны, квадратичная форма отрицательно определена, когда первый угловой минор отрицательный, а далее знаки чередуются +,-.
2) Задачи выпуклого программирования. Задачей выпуклого программирования называется задача нелинейного программирования, у которой все функции являются выпуклыми функциями. Общая задача выпуклого программирования состоит в отыскании такого вектора х (т. е. такой точки выпуклого допустимого множества), который является минимум выпуклой функции 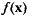
3) Функция Лагранжа, принцип ее построения.
F(x1,x2…xn, λ1…λm)=f(x1…xn)+ 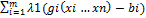
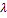
4) Метод множителей Лагранжа позволяет находить экстремум функции при ограничениях – равенствах.
— Составляется функция Лагранжа.
— Определяются частные производные функции Лагранжа по всем переменным и приравниваются к 0. В итоге получается система из n+m уравнений с n+m неизвестными, решая эту систему уравнений получаем точки подозрительные на экстремум.
Найденные точки дальше исследуются на минимум или максимум.
Дальнейшее исследование проводится как в случае безусловной оптимизации, т.е строится матрица вторых производных и сравниваются значения главных миноров.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
 ;
;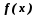 на множестве
на множестве ). Нижней оценкой будет такое число
). Нижней оценкой будет такое число , что
, что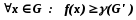 ;
; на подмножества(ветвление по определенным правилам);
на подмножества(ветвление по определенным правилам); , то
, то . Если множество
. Если множество состоит из объединения
состоит из объединения , то есть
, то есть , то оценка для любого подмножества
, то оценка для любого подмножества будет не меньше, чем оценка для множества
будет не меньше, чем оценка для множества , то есть:
, то есть:
 . Если удается найти такоеx, что
. Если удается найти такоеx, что  , тоx — оптимальное решение. Если оптимальное решение не обнаружено, то по некоторому правилу разбиваем множество
, тоx — оптимальное решение. Если оптимальное решение не обнаружено, то по некоторому правилу разбиваем множество  на подмножества
на подмножества ;
; множеств
множеств . Если при этом удается найти такоеx, что
. Если при этом удается найти такоеx, что  ,
, , тоx — оптимальное. Если такого x не обнаружили, то для дальнейшего разбиения выбираем множество
, тоx — оптимальное. Если такого x не обнаружили, то для дальнейшего разбиения выбираем множество  с минимальной оценкой. Разбиваем это множество на несколько подмножеств и повторяем процесс до тех пор, пока не получим оптимальное решение.
с минимальной оценкой. Разбиваем это множество на несколько подмножеств и повторяем процесс до тех пор, пока не получим оптимальное решение.