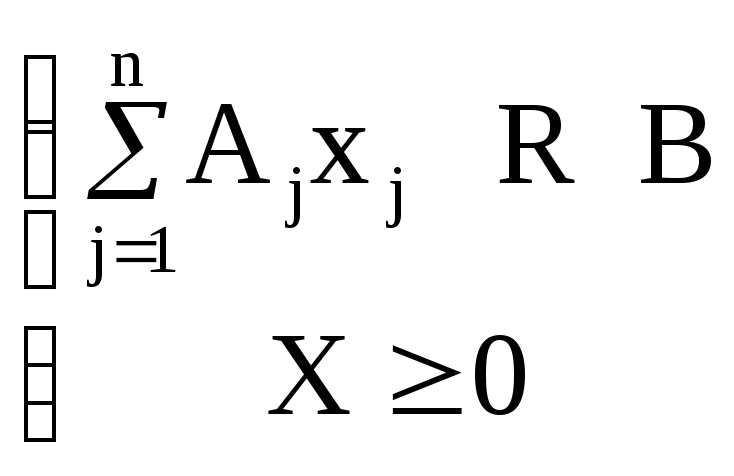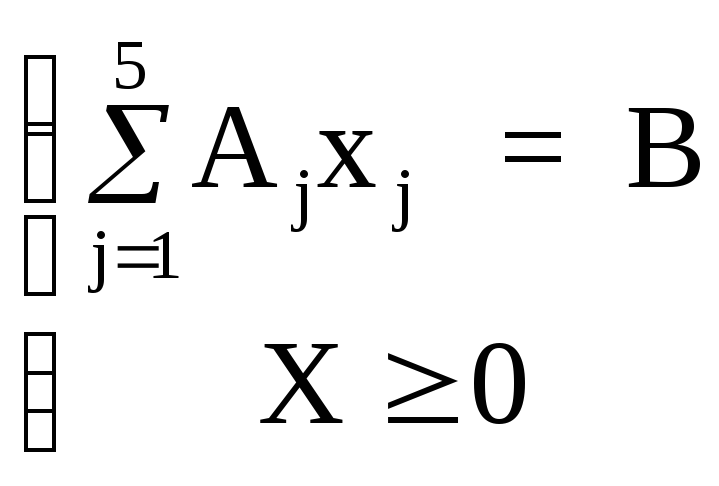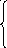Опорный план матрицы задачи линейного программирования

Решение задач линейного программирования

Назначение сервиса . Онлайн-калькулятор предназначен для решения задач линейного программирования симплексным методом путем перехода к КЗЛП и СЗЛП . При этом задача на минимум целевой функции сводятся к задаче на поиск максимума через преобразование целевой функции F*(X) = -F(X) . Также имеется возможность составить двойственную задачу.

1. Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
2. Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
3. Решение симплексным методом;

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word .

Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:

F(x) → min

F(x) → max

Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (x_m+1,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Пример №1 . Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x₁ + 2x₂ — 2x₃ → min при ограничениях:
4x₁ + 3x₂ — x₃≤10
— 2x₂ + 5x₃≥3
x₁ + 2x₃=9
Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции. Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1). В первом неравенстве смысла (≤) вводим базисную переменную x₄; во втором неравенстве смысла (≥) вводим базисную переменную x₅ со знаком минус.
4x₁ + 3x₂-1x₃ + 1x₄ + 0x₅ = 10
0x₁-2x₂ + 5x₃ + 0x₄-1x₅ = 3
1x₁ + 0x₂ + 2x₃ + 0x₄ + 0x₅ = 9
F(X) = — x₁ — 2x₂ + 2x₃
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

4	3	-1	1	0	10
0	-2	5	0	-1	3
1	0	2	0	0	9

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₄.
2. В качестве базовой переменной выбираем x₂.
Разрешающий элемент РЭ=-2. Строка, соответствующая переменной x₂, получена в результате деления всех элементов строки x₂ на разрешающий элемент РЭ=-2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₂ записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:

4-(0 • 3):-2	3-(-2 • 3):-2	-1-(5 • 3):-2	1-(0 • 3):-2	0-(-1 • 3):-2	10-(3 • 3):-2
0 : -2	-2 : -2	5 : -2	0 : -2	-1 : -2	3 : -2
1-(0 • 0):-2	0-(-2 • 0):-2	2-(5 • 0):-2	0-(0 • 0):-2	0-(-1 • 0):-2	9-(3 • 0):-2

Получаем новую матрицу:

4	0	6 1 /2	1	-1 1 /2	14 1 /2
0	1	-2 1 /2	0	1 /2	-1 1 /2
1	0	2	0	0	9

3. В качестве базовой переменной выбираем x₃.
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x₃, получена в результате деления всех элементов строки x₃ на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₃ записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:

4-(1 • 6 1 /2):2	0-(0 • 6 1 /2):2	6 1 /2-(2 • 6 1 /2):2	1-(0 • 6 1 /2):2	-1 1 /2-(0 • 6 1 /2):2	14 1 /2-(9 • 6 1 /2):2
0-(1 • -2 1 /2):2	1-(0 • -2 1 /2):2	-2 1 /2-(2 • -2 1 /2):2	0-(0 • -2 1 /2):2	1 /2-(0 • -2 1 /2):2	-1 1 /2-(9 • -2 1 /2):2
1 : 2	0 : 2	2 : 2	0 : 2	0 : 2	9 : 2

Получаем новую матрицу:

3 /4	0	0	1	-1 1 /2	-14 3 /4
1 1 /4	1	0	0	1 /2	9 3 /4
1 /2	0	1	0	0	4 1 /2

Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,2,3).
Соответствующие уравнения имеют вид:
3 /₄x₁ + x₄ — 1 1 /₂x₅ = -14 3 /₄
1 1 /₄x₁ + x₂ + 1 /₂x₅ = 9 3 /₄
1 /₂x₁ + x₃ = 4 1 /₂
Выразим базисные переменные через остальные:
x₄ = — 3 /₄x₁ + 1 1 /₂x₅-14 3 /₄
x₂ = — 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄
x₃ = — 1 /₂x₁+4 1 /₂
Подставим их в целевую функцию:
F(X) = — x₁ — 2(- 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄) + 2(- 1 /₂x₁+4 1 /₂)
или
F(X) = 1 /₂x₁ + x₅-10 1 /₂ → max
Система неравенств:
— 3 /₄x₁ + 1 1 /₂x₅-14 3 /₄ ≥ 0
— 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄ ≥ 0
— 1 /₂x₁+4 1 /₂ ≥ 0
Приводим систему неравенств к следующему виду:
3 /₄x₁ — 1 1 /₂x₅ ≤ -14 3 /₄
1 1 /₄x₁ + 1 /₂x₅ ≤ 9 3 /₄
1 /₂x₁ ≤ 4 1 /₂
F(X) = 1 /₂x₁ + x₅-10 1 /₂ → max
Упростим систему.
3 /₄x₁ — 1 1 /₂x₂ ≤ -14 3 /₄
1 1 /₄x₁ + 1 /₂x₂ ≤ 9 3 /₄
1 /₂x₁ ≤ 4 1 /₂
F(X) = 1 /₂x₁ + x₂-10 1 /₂ → max

Источник

3 Симплекс-метод решения задачи линейного программирования

Графический способ решения задачи линейного программирования целесообразно использовать для задач небольшой размерности (с двумя переменными) или задач, которые могут быть сведены к задачам с двумя переменными. Можно строить и трехмерные графики, хотя это уже несколько сложнее. Достоинствами этого метода являются его простота и наглядность. Однако на практике при построении экономико-математических моделей обычно вводится большее количество переменных, что делает необходимым использование более сложных методов.

Симплекс-методпредставляет собой общий аналитический метод решения задачи линейного программирования * .

Так же, как и при использовании графического способа решения, идея симплекс-метода состоит в рассмотрении вершин области допустимых планов (ОДП) в многомерном пространстве и в определении на основании некоторого критерия, является ли рассматриваемый план оптимальным.

При этом симплекс-метод предлагает алгоритм такого направленного перебора этих вершин, при котором нет необходимости рассматривать их все, поскольку при переходе от одного плана к другому происходит приближение к искомому решению (или установление неразрешимости).

Однако, если при использовании графического метода вершины ОДП можно было определить визуально, то в симплекс-методе это уже можно сделать только аналитически. Поэтому для описания алгоритма рассматриваемого метода необходимо ввести некоторые понятия.

3.1 Векторная запись задачи линейного программирования. Опорный план

Система ограничений задачи линейного программирования, приведенной к канонической или стандартной форме, может быть записана в векторной формеследующим образом:

где А_j =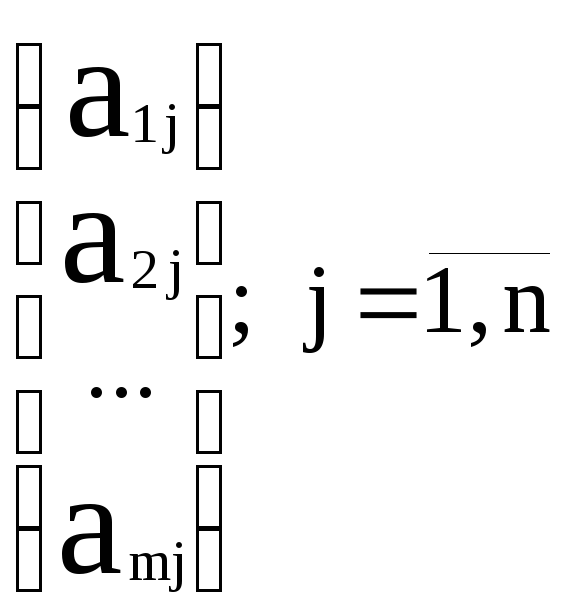— векторные коэффициенты; B= , X=,R.

Будем считать, что система ограничений задачи в канонической форме представляет собой линейно независимую систему уравнений (в противном случае часть уравнений можно просто вычеркнуть).

Опорным планомзадачи линейного программирования в канонической форме называется такой допустимый план, совокупность векторных коэффициентов при ненулевых компонентах которого представляет собой систему линейно независимых векторов * .

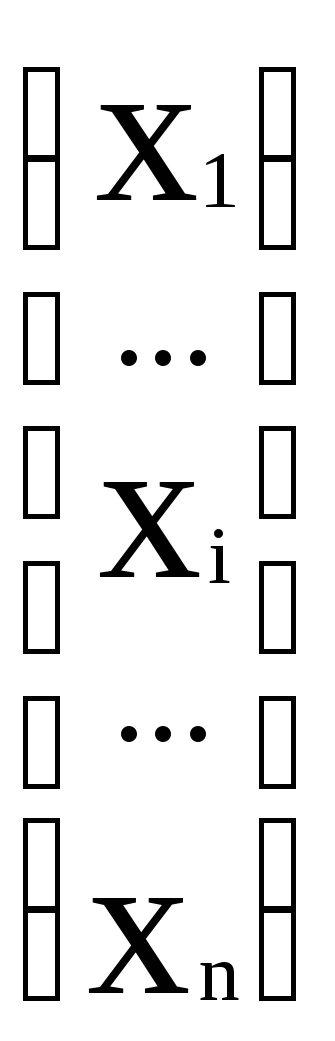
Например, представим систему ограничений задачи, записанной в канонической форме, в векторной форме:

А₁=, А₂=, А₃=, А₄=, А₅=, В =, Х =;

.

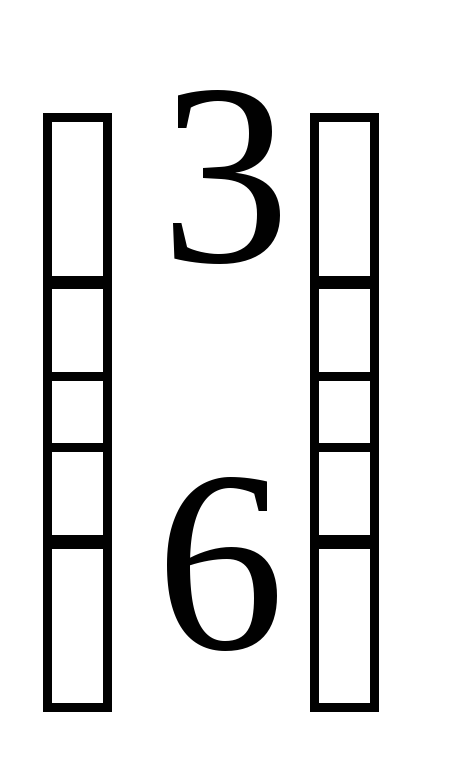
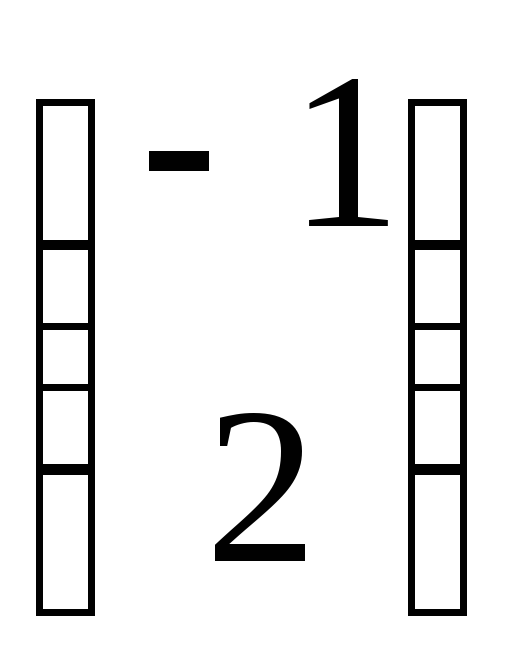
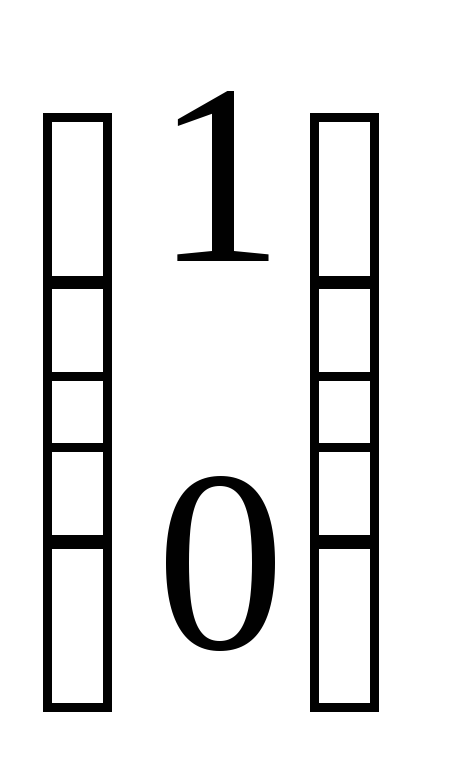
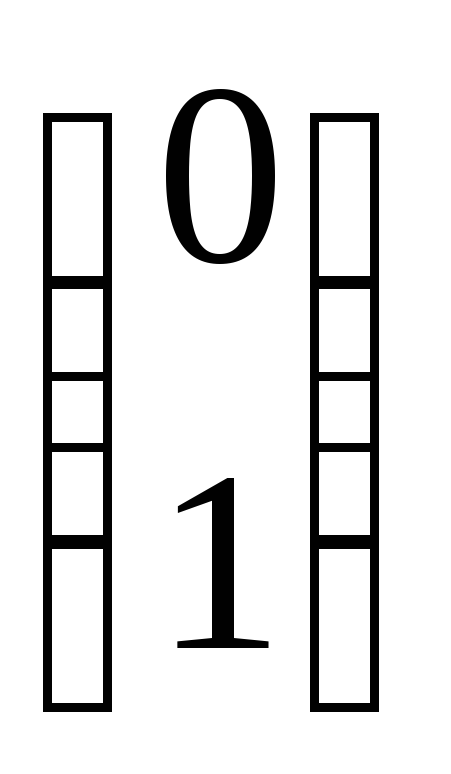
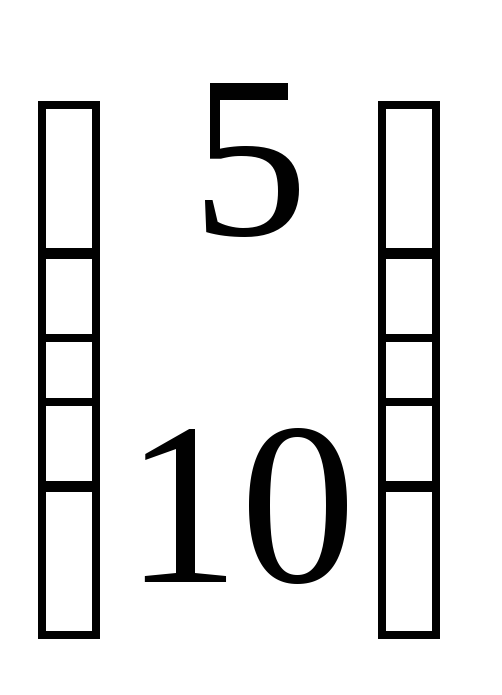
Рассмотрим план Х (1) = (0; 0; 0; 5; 10). Этот план является допустимым, в чем легко убедиться, подставив его в систему ограничений:

2*0 + 3*0 — 0 + 5 = 5

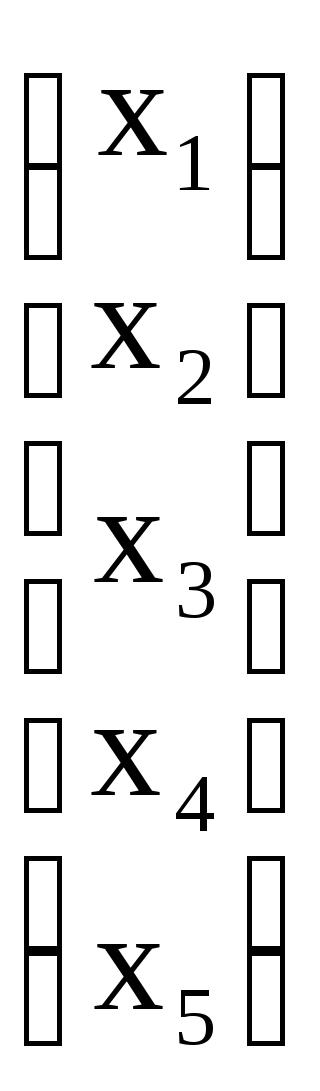
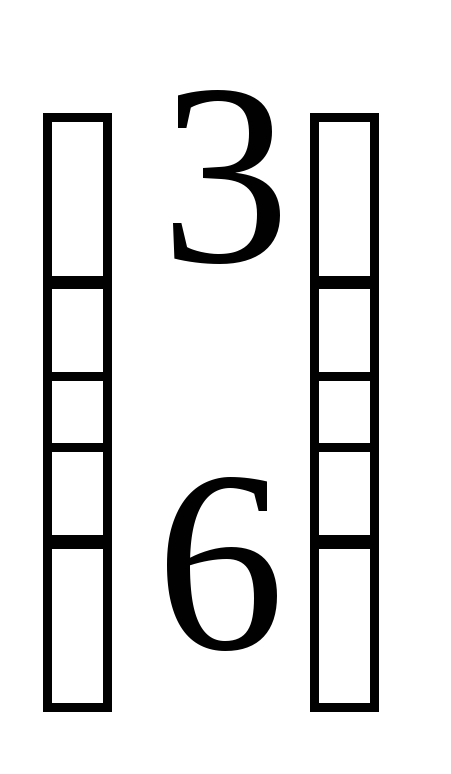
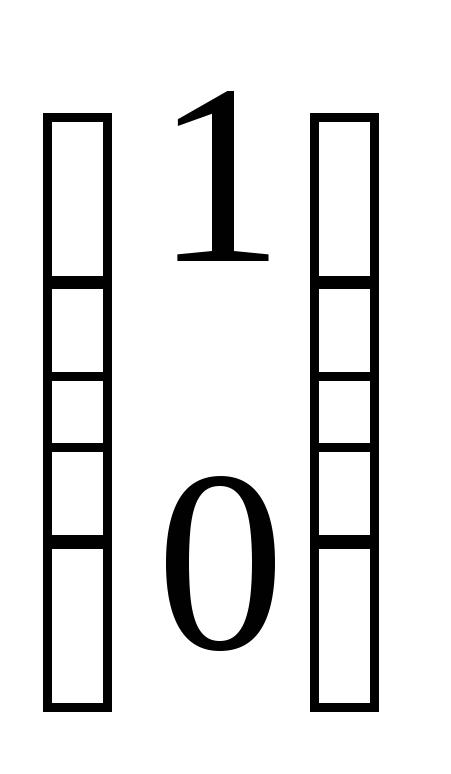
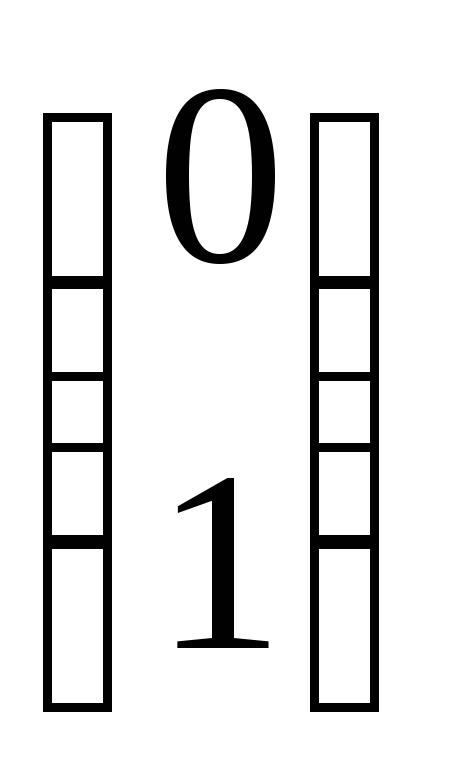
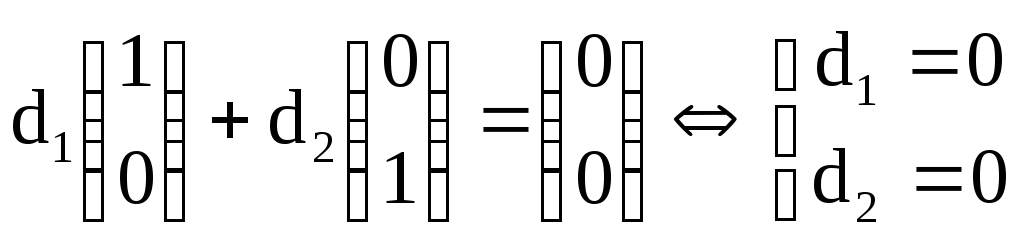
Отличными от нуля являются переменные х₄ и х₅. Векторные коэффициенты при этих переменных А₄=и А₅=являются линейно независимыми. В самом деле,. Следовательно, план Х (1) является опорным.

Убедимся в том, что отнюдь не любой допустимый план является опорным. Для этого рассмотрим другой план Х (2) = (1; 1; 0; 0; 0). Здесь ненулевыми компонентами плана являются переменные х₁ и х₂. Этот план тоже является допустимым:

4*1 + 6*1 + 2*0 + 0 = 10

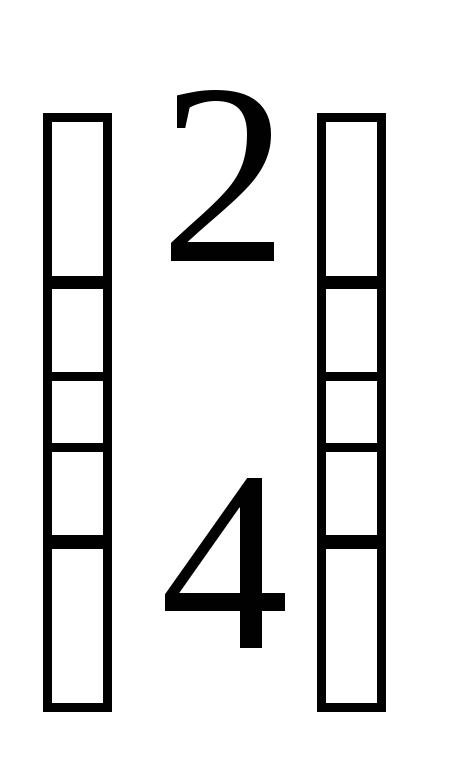
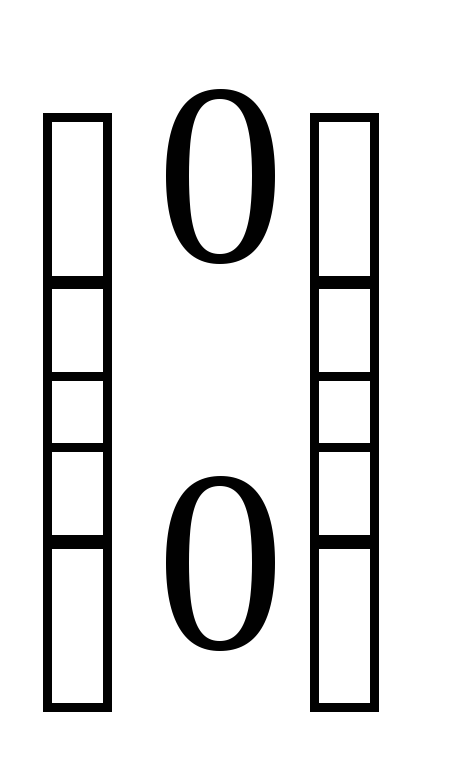
Однако этот план не является опорным, так как можно подобрать отличные от нуля числа d₁и d₂, при которых d₁А₁+ d₂А₂ = d₁+d₂=. Таких чисел бесконечно много, например, d₁= 3, d₂= -2.

Можно доказать [6], что каждой вершине ОДП задачи линейного программирования соответствует опорный план. Поэтому, чтобы найти оптимальный план в одной из вершин, симплекс-метод перебирает именно опорные планы задачи линейного программирования.

Очевидно, что ненулевых компонент в опорном плане может быть не больше, чем ограничений в задаче (в рассмотренном примере невозможно построить три двумерных линейно независимых вектора, поэтому ненулевых компонент не может быть больше двух). Для реализации симплекс-метода необходимо, чтобы в опорном плане присутствовало ровно mлинейно независимых векторов, т.е. базисm–мерного пространства. В случае, если ненулевых компонент в опорном плане меньше, чемm, один или несколько из этих векторов могут соответствовать и нулевым переменным.Переменные, столбцы коэффициентов при которых образуют полную систему (m) единичных независимых столбцов, будем называтьбазисными(х_Б), а остальные переменные —небазисными.Столбцы (вектора), соответствующие базисным переменным, также будем называтьбазисными. Совокупность этих переменных (или этих векторов) будем называтьбазисом. Если среди базисных переменных есть нулевые, базис называютвырожденным.

Например, в плане Х (1) в базис входили переменные х₄ и х₅, и базис был невырожденным.

Источник