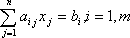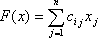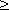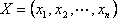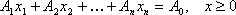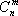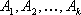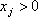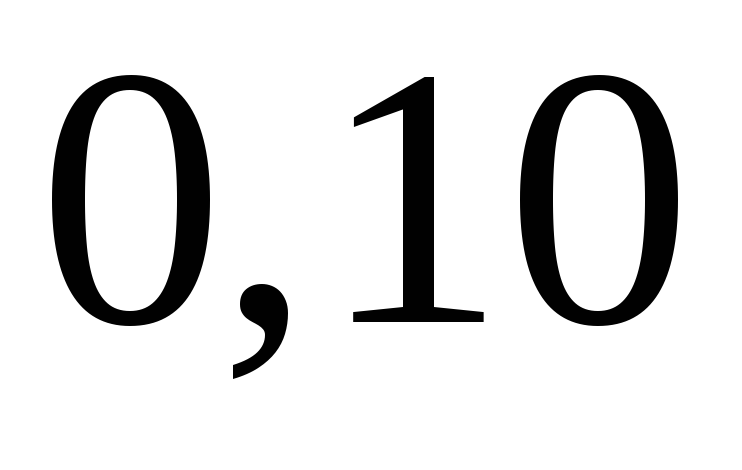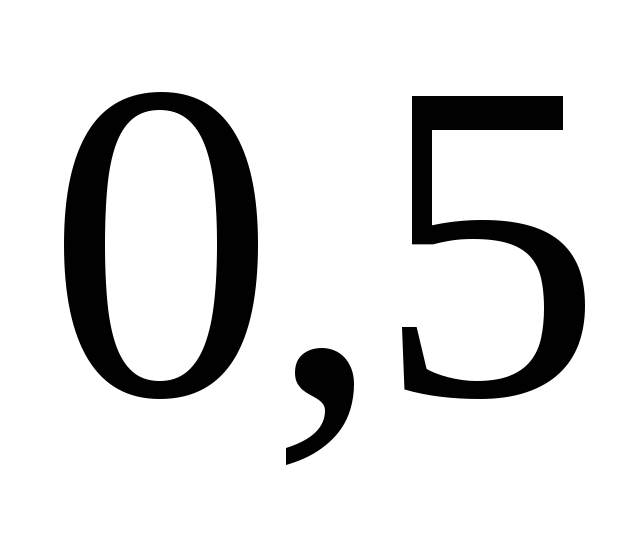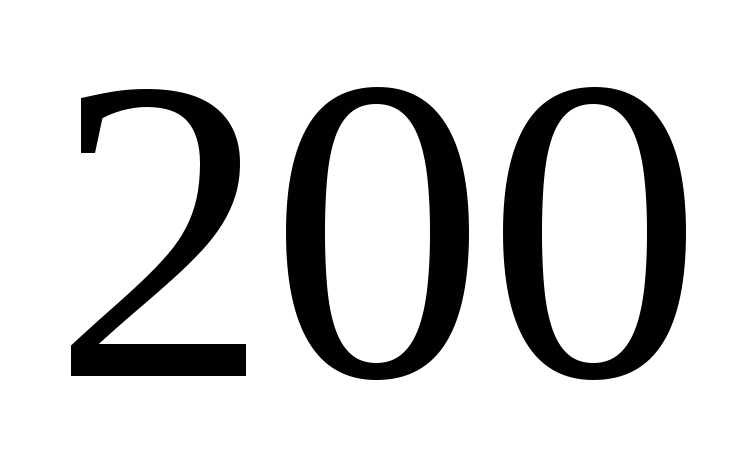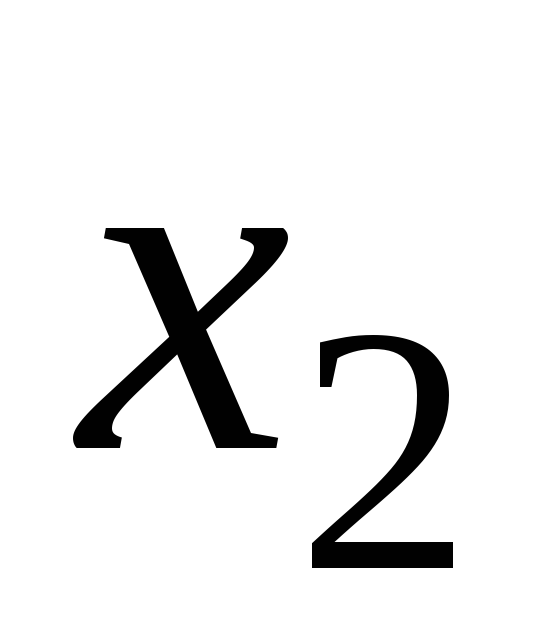Опорным решением задачи линейного программирования является

Общая задача линейного программирования.

3) цель задачи ()

(max F(x))

(min F(x))

Определение: Планом или допустимым решением задачи линейного программирования называется вектор , удовлетворяющий условиям 1) и 2)

(*)

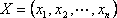
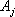
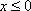
Определение: План называетсяопорным, если векторы , входящие в разложение (*) с положительными коэффициентами, являются линейно независимыми.

Определение: Опорный план называется невырожденным, если он содержит m – положительных компонентов, в противном случае опорный план называется вырожденным.

Определение: Оптимальным планом (решением) задачи линейного программирования называется план, доставляющий линейной форме наибольшее или наименьшее значение.

В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, либо система ограничений смешанная, однако любую систему ограничений можно привести к системе уравнений. Для этого достаточно к левой части каждого неравенства прибавить (для ) или отнять (для) какое-то неотрицательное число (добавочную переменную) с тем, чтобы каждое неравенство обратилось в уравнение, в результате получим эквивалентные системы уравнений и неравенств.

Основные теоремы линейного программирования

Теорема 1: Множество всех допустимых решений системы ограничений задачи линейного программирования, является выпуклым.

Теорема 2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , гдеn — число неизвестных , а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.

Теорема 3: Если известно, что система векторов в разложении линейно независима и такова, что, где, то точкаявляется угловой точкой многогранника решений.

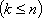
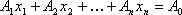
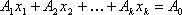
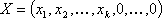
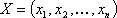
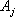
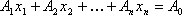
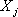
Теорема 4: Если — угловая точка многогранника решений, то векторыв разложении, соответствующие положительным, являются линейно независимыми.

Следствие 1: Так как векторы 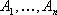имеют размерностьm, то угловая точка многогранника решений имеет не более m положительных компонент .

Следствие 2: Каждой угловой точке многогранника решений соответствует линейно независимых векторов системы векторов.

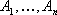
Симплексный метод решения задачи линейного программирования.

Доказано, что оптимальное решение задачи линейного программирования связано с угловыми точками многоугольника решений, то есть с опорными планами. Они определяются системой m — линейно независимых векторов, содержащихся в системе из n — векторов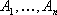. Количество опорных планов меньше, гдеn — число неизвестных, а m – число ограничений. При больших n и m найти все их перебором очень трудно, поэтому необходимо упорядоченный перебор, такой схемой является симплексный метод, который позволяет исходя из известного опорного плана задачи, за конечное число шагов получить её оптимальный план. Каждый из шагов (итераций) состоит в нахождении нового плана, которому соответствует меньшее для задачи на минимум (большее для задачи на максимум) значение линейной формы, чем её значение в предыдущем плане. Процесс продолжается до получения оптимального плана. Если задача не обладает планами или её линейная форма неограниченна на многограннике решений, то симплексный метод позволяет установить это в процессе решения.

Источник

4.4. Опорное решение задачи линейного программирования,

Рассмотрим каноническую задачу ЛП в векторной записи (см.(2.1.2)):

, ,(4.4.1)

.

Определение 4.4.1.Опорным решением задачи ЛПназывается такое допустимое решение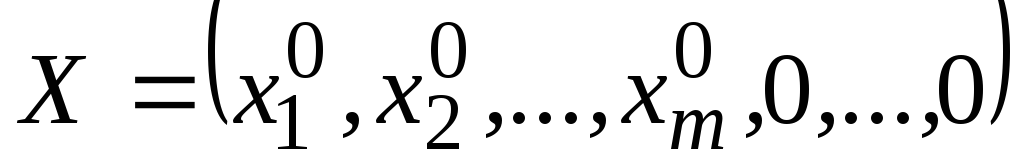, для которого соответствующие положительным координатамвекторы,,…,в (4.4.1) линейно независимы.

Число отличных от нуля координат опорного решения не может быть больше ранга системы векторов условия (т.е. числа линейно независимых уравнений системы ограничений). В дальнейшем будем считать, что система ограничений состоит из линейно независимых уравнений, т.е.. Если число отличных от нуля координат опорного решения равно, то оно (решение) называется невырожденным, в противном случае (меньшевырожденным.

Определение 4.4.2.Базисом опорного решения называется базис системы векторов условия задачи (4.4.1), в состав которого входят векторы, соответствующие отличным от нуля координатам опорного решения.

Приведём без доказательства две теоремы о взаимосвязи опорных решений и угловых точек множества допустимых решений.

Теорема 4.4.1.Любое опорное решение является угловой точкой области допустимых решений.

Теорема 4.4.2.Любая угловая точка области допустимых решений является опорным решением.

Доказательства теорем 4.4.1 и 4.4.2 проводятся методом от противного (см. [3], с.537-539).

5. Симплексный метод решения задач

Симплексный метод – это метод целенаправленного перебора опорных решений задачи ЛП. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что его не существует. Основное содержание метода состоит в следующем:

1. Указать способ нахождения начального опорного плана.

2. Указать способ перехода от одного опорного плана к другому, на котором значение целевой функции ближе к оптимальному.

3. Задать критерии, которые позволяют своевременно прекратить проверку решений на оптимальность или сделать заключение об отсутствии оптимального решения.

5.1. Нахождение начального опорного плана и переход к новому опорному решению

Предположим, что необходимо найти минимум целевой функции при следующей системе ограничений:

(5.1.1)

Запишем систему (5.1.1) в векторной форме:

(5.1.2)

, ,…,,. .

Векторы ,. образуют базис в. Поэтому в соотношении (5.1.2) за базисные переменные принимаем,,…,, а остальные переменные

(будем называть их свободными) приравниваем нулю. Учитывая, что , получаем, что опорное решение задачи (5.1.1) имеет вид

Рассмотрим, как, исходя из начального опорного решения, можно построить другое опорное решение, которое будет более близким к оптимальному, т.е. на котором значение целевой функции будет меньше. Систему ограничений (5.1.1) перепишем в виде:

(5.1.3)

Выражая значения ,,…,через свободные неизвестные, целевую функциюполучим в виде:

. (5.1.4)

Итак, первоначальный опорный план , а соответствующее значение. Возможны следующие ситуации:

1) все ,, …,. Тогда минимумдостигается при, т.е. планявляется оптимальным и;

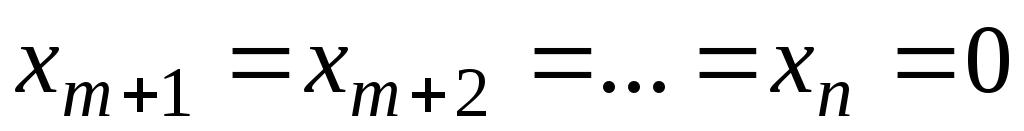
2) среди чисел ,, …,имеются положительные. Пусть, гдеодно из чисел,. ;,. Тогда полагаем все,, …,равными нулю, кроме. Из (5.1.3) следует, что

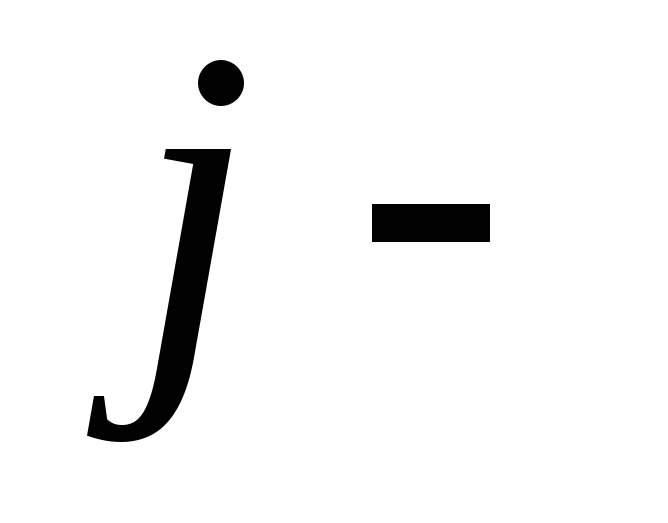
(5.1.5)

и .

Здесь, в свою очередь, могут представиться два случая:

а) все числа ,, …,, тогда для любоговсе значения,,…,. В этом случаене достигается, так как прифункция;

б) среди чисел ,, …,имеются положительные. Пусть, например,. Так как все компоненты плана должны быть положительны, тонельзя увеличивать более, чем( иначестанет отрицательным ).

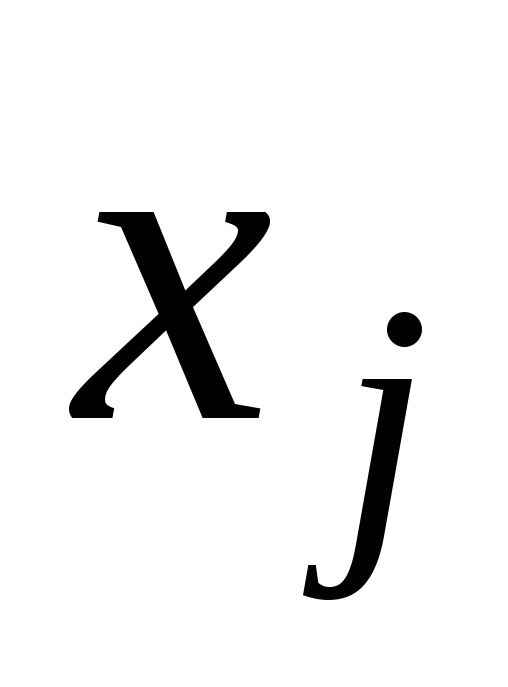
Поэтому найдём называется разрешающим элементом. Положим,…,,,,…,. Найдём значения остальных неизвестных:

Получено новое опорное решение: .

Значение целевой функции при этом уменьшается:

.

Идея симплекс-метода заключается в том, что на каждом этапе один из векторов выводится из базиса, а вместо него вводится другой –. При этом удобно, чтобы он стал бы единичным. Поэтому в системе ограничений-е уравнение, содержащее разрешающий элемент, делим на. Исключаемиз всех остальных уравнений, т.е. осуществляем преобразование Жордана-Гаусса.

Итак, алгоритм симплекс-метода состоит в следующем:

1. Приводим систему к виду, содержащему единичных векторов, и определяем первоначальный опорный план.

2. Выражаем через свободные переменные в виде:

.

Если при этом все коэффициенты ,. не являются положительными, то найденный первоначальный план являетсяоптимальным.

3. Пусть среди чисел ,. имеются положительные. Берём любой из них, например,, и просматриваем весь соответствующий столбец. Он называется разрешающим столбцом. Если все числа этого столбца отрицательны, тоЗадача решения не имеет.

4. Если в этом столбце есть положительные числа, то находим разрешающий элемент – это элемент, для которого отношениеминимально. Пусть это элемент.

5. Выводим переменную из числа свободных и меняем её с базисной переменной.

6. Эту процедуру выполняем до тех пор, пока все коэффициенты при свободных неизвестных станут неположительными, (это признак

оптимальности плана) либо неположительными станут все элементы в разрешающем столбце ( т.е. ).

Замечание. На практике этот алгоритм реализуется с помощью симплекс-таблиц (см. пример 5.1.).

Пример 5.1. Строительное управление ведёт капитальный ремонт жилых домов. Перегородки внутри этих домов могут быть изготовлены гипсобетонными или каркасными ( с обшивкой листами сухой штукатурки ). Ресурсы на месяц заданы в таблице:

Потребности на площади перегородок

чел. дней

чел. дней

Рассчитать общее количество как каркасных, так и гипсобетонных перегородок, которые следует возвести в текущем месяце, чтобы их площадь была наибольшей, если строительное управление имеет в наличии гипсобетона –, пиломатериалов –, сухой штукатурки –, трудоресурсов –.

Решение. Составим математическую модель задачи. Пусть требуется возвести каркасных игипсобетонных перегородок. Из условия на это уйдёт: гипсобетона, пиломатериалов, сухой штукатурки, трудоресурсов. Учитывая лимиты материалов и трудоресурсов, составляем систему ограничений – неравенств:

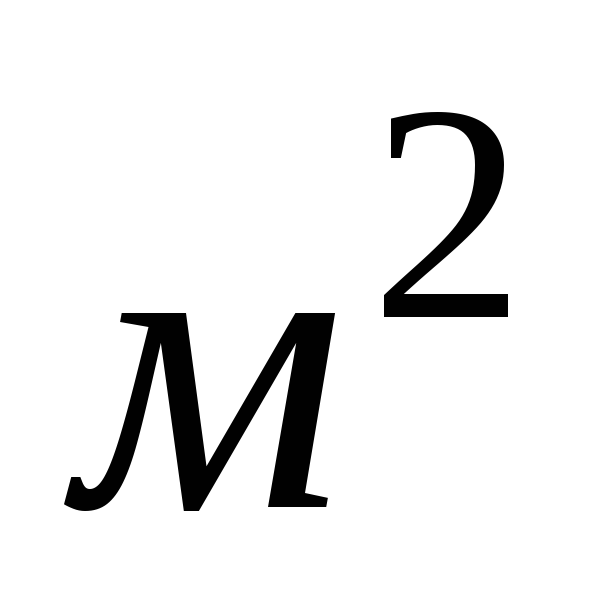
Для решения задачи симплекс-методом вводим дополнительные переменные:

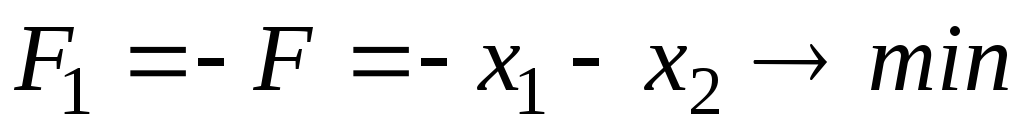
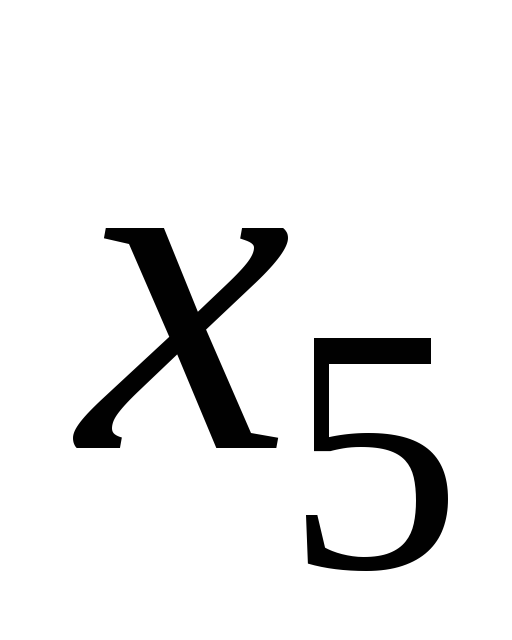
Полагаем . Принимаем,в качестве свободных переменных,,,,в качестве базисных. Начальный опорный план имеет вид:,. Составляем симплекс-таблицу (в сокращённой форме), соответствующую начальному опорному плану. Обратим внимание, что коэффициенты при свободных переменных пишутся с противоположным знаком.

—

—

Источник