Операции над графами
При решении поставленной задачи для представления графа был выбран список смежности.
type TUk1=^TEl1; //элемент списка вершин
TEl=record //элемент списка смежности
Head:TUk; //указатель на начало списка
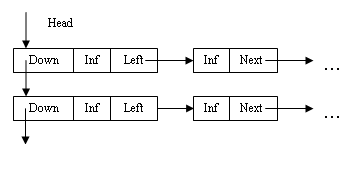
Схематичное представление списка смежности ориентированного графа представлено на рисунке 2.1
Рисунок 2.3 – Схема списка смежности
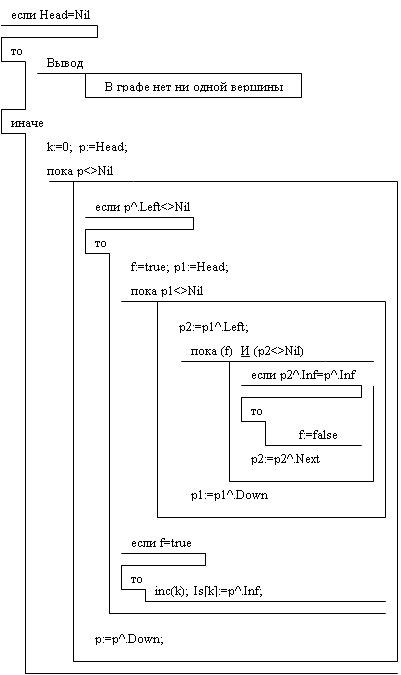
Алгоритм нахождения источников ориентированного графа представлен на рисунке 2.4.
Рисунок 2.4 — Алгоритм нахождения источников орграфа
2.3 Описание программной реализации
2.3.1 Описание процедур и функций языка
Процедура New – резервирует фрагмент кучи для размещения переменной; формат обращения
TP – типизированный указатель. За одно обращение к процедуре можно зарезервировать не более 65521 байт динамической памяти. Если нет свободной памяти требуемого размера, возникает ошибка периода исполнения. Если память не фрагментирована, последовательные обращения к процедуре будут резервировать последовательные участки памяти, так что начало следующего будет располагаться сразу за концом предыдущего.
Процедура Dispose – возвращает в кучу фрагмент динамической памяти, который ранее был зарезервирован за типизированным указателем; формат обращения
TP – типизированный указатель. При повторном использовании процедуры применительно к уже освобожденному фрагменту возникает ошибка периода исполнения.
2.3.2 Описание функций работы с динамической памятью, графами
Для решения поставленной задачи были разработаны следующие процедуры и функции:
1) procedure AddVer(n:integer); — добавление в список смежности вершины с номером n;
2) procedure AddDug(n,m:integer); — добавление в список дуги (n,m). n и m номера вершин источника дуги и стока соответственно;
3) procedure DelList(p:TUk1); — удаление списка смежных вершин. p – указатель на начало списка;
4) procedure DelVer(n:integer); — удаление вершины с номером n;
5) procedure DelDug(n,m:integer); — удаление дуги (n,m). n и m номера вершин источника дуги и стока соответственно;
6) procedure PrintGraph; — вывод списка смежности на экран в виде матрицы смежности;
7) procedure FindIstok; — поиск и вывод на экран всех источников орграфа.
Задание, выданное на летнюю практику, поставило определенные задачи:
1) научится создавать связные структуры данных, используя указатели;
2) научится создавать и манипулировать динамическими структурами данных, такими как связные списки, очереди и стеки;
3) понять работу различных приложений со связными структурами данных.
Решение выданного задания было реализовано с помощью языка программирования Паскаль.
Во время прохождения учебной практики был закреплен теоретический материал по разработке динамических структур данных, были получены практические навыки реализации динамических структур данных на языке высокого уровня для представления и обработки графов.
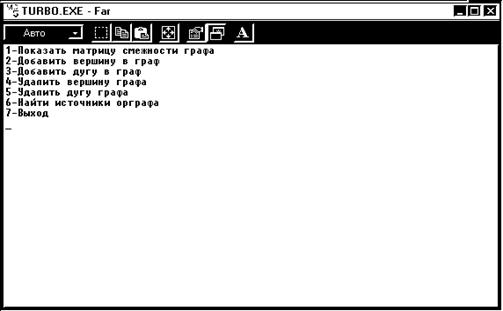
Рисунок А.1 – Главное меню программы
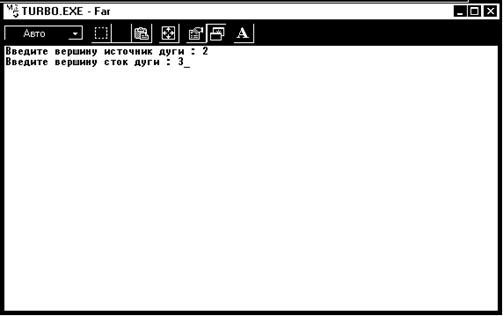
Рисунок А.2 – Добавление дуги орграфа
Рисунок А.3 – Матрица смежности орграфа
Рисунок А.4 – Список вершин источников орграфа
Вступление
Как оказалось тема алгоритмов интересна Хабра-сообществу. Поэтому я как и обещал, начну серию обзоров «классических» алгоритмов на графах.
Так как публика на Хабре разная, а тема интересна многим, я должен начать с нулевой части. В этой части я расскажу что такое граф, как он представлен в компьютере и зачем он используется. Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.
Основы
В математике, Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).
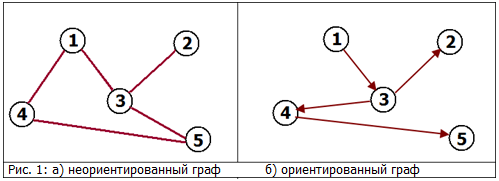
Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1). См рис. 1.а
Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б
Степень вершины может быть входящая и исходящая (для неориентированных графов входящая степень равна исходящей).
Входящая степень вершины v это количество ребер вида (i, v), то есть количество ребер которые «входят» в v.
Исходящая степень вершины v это количество ребер вида (v , i), то есть количество ребер которые «выходят» из v.
Это не совсем формальное определение (более формально определение через инцидентность), но оно вполне отражает суть
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].
У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.
Представление графов
Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.
Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V| 2 ).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
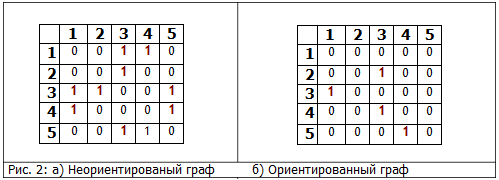
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u].
С другой стороны этот способ очень громоздкий, так как требует O (|V| 2 ) памяти для хранения матрицы.
На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.
Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).
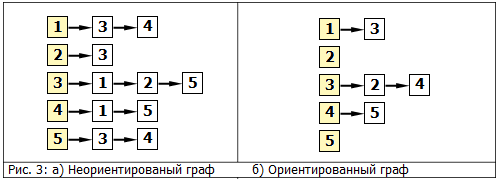
На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.
Применение
Те кто дочитал до этого места, наверное задали себе вопрос, а где же собственно я смогу применить графы. Как я и обещал я буду стараться приводить примеры. Самый первый пример который приходит в голову это социальная сеть. Вершинами графа являются люди, а ребрами отношения (дружба). Граф может быть неориентированным, то есть я могу дружить только с теми кто дружит со мной. Либо ориентированным (как например в ЖЖ), где можно добавить человека в друзья, без того чтобы он добавлял вас. Если же он да добавит вас вы будете «взаимными друзьями». То есть будет существовать два ребра: (Он, Вы) и (Вы, Он)
Ещё одно из применений графа, которое я уже упоминал это ссылки с сайта на сайт. Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)
Заключение
Это небольшая часть теории которая понадобится нам чтобы для следующих частей. Надеюсь вам было понятно, а главное понравилось и заинтересовало читать дальнейшие части! Оставляйте свои отзывы и пожелания в комментариях.
В следующей части
BFS — Алгоритм поиска в ширину
Библиография
Кормен, Лайзерсон, Риверст, Штайн — Алгоритмы. Построение и анализ. Издательство Вильямс, 2007.
Словарь терминов теории графов
Граф — статья в английской Википедии
Статья это кросс-пост из моего блога — «Programing as is — записки программиста»