Одз задача линейного программирования

5. Формы представления задач линейного программирования

1. Стандартная форма на максимум:

1. Стандартная форма на минимум:

1. Каноническая форма представления:

6. Структура допустимого множества и типы решений задач линейного программирования

Каждое функциональное ограничение, входящее в формальную запись задачи линейного программирования, представляет собой некоторые замкнутые полупространства размерности n (при условии ограничения в виде неравенства). Если ограничения заданы в виде равенства, то оно отображается гиперплоскостью в n-мерном пространстве. Прямые ограничения образуют также замкнутые полупространства. Следовательно, допустимое множество задач линейного программирования задается системой ограничений и представляет собой пересечение замкнутых полупространств и/или гиперплоскостей. Такое образование называетсямногогранным множеством. Многогранное множество всегда замкнуто и выпукло, но в частном случае может быть пустым или неограниченным, а размерность его может составлять n или менее. Рассмотрим примеры формирования допустимого множества для n=2, тогда все рассуждения будут рассматриваться на плоскости. Пример 1 Данная система решений не имеет (т.к. нет пересечений), следовательно, Х а =. Пример 2. Данная система имеет решение в точке (3,0), следовательно, Х а =(3,0). Пример 3. Областью допустимых значений Х а в данном случае является отрезок. Пример 4. Областью допустимых значений Х а в данном случае является ограниченная область. Пример 5. Областью допустимых значений Х а в данном случае является неограниченная область.

7. Типы решений

Если считать, что целевая функция задачи линейного программирования имеет вид f(x₁, …, x_n) = c₁x₁ + … + c_nx_n = C, то эта целевая функция представляет собой семейство параллельных гиперплоскостей в n-мерном пространстве. Если требуется максимизировать целевую функцию, то при графической задаче константа С увеличивается, пока гиперплоскость все еще будет пересекать допустимое множество, т.е.: Δf=(c₁, …, c_n) – градиент целевой функции.Если требуется минимизировать целевую функцию, то гиперплоскость надо сдвигать в направлении противоположном градиенту. Возможны следующие случаи:

1. Задача не имеет решений

1. Задача имеет единственное решение

1. Задача имеет единственное решение

1. Задача имеет множество решений

8. Понятие двойственной задачи

Если имеется задача линейного программирования на max: 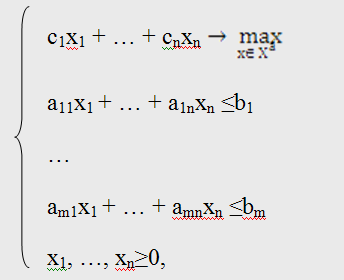то механизм построения двойственной задачи заключается в следующем: это двойственная задача. Связь прямой и двойственной задачи состоит в том, что решение одной из них может быть получено из решения другой. Теоретически доказано, что прямая и двойственная задача либо обе неразрешимы, либо обе имеют решение, причем значения целевых функций для оптимальных решений совпадают. На практике бывают случаи, когда решение двойственной задачи оказывается проще, чем прямой.

9. О методах решения задач линейного программирования

Для задач линейного программирования, особенно для типовых классов таких задач, разработано много специфических методов, причем эти методы часто связаны с решением двойственных задач. Однако, несмотря на специфику различных методов, практически все они реализуют общий метод решения задач линейного программирования, названный симплекс-методом (метод последовательного улучшения оценок). Он был предложен Данцингом в 1947 г. Геометрический метод состоит в следующем: пусть имеется n-переменных х_{1, …,} х_n и p-ограничений, p процесс регуляризации.

Источник

Теоретические основы поиска оптимального решения задачи линейного программирования.

ОДЗ – область допустимых значений. Теорема 1: если есть ОДЗ, то она всегда выпукла. Теорема 2: поиск оптимальных решений задачи следует осуществлять в вершинах ОДЗ.

Достоинства и недост лин. Моделей задачи планированияпроизв-ти.

1)Снижена трудоёмкость за счёт пренебрежения зависимостью коэф целевой ф-ции или части ограничений (парам моделей) от оптимизируемых величин.

2)прим-е для реш-я большого количества плановых задач, причём форма задач во многих случаях повторяется, задачи одного класса возникают в разл отраслях горпром-ти, сферах деят-ти гор предприятия

Графический метод решения задачи лп.

1)В принятой системе координат построить Ур-я всех ограничений, суммы которых даст многоугольник (многогор) ограничений.

2)Построить уравнение целевой функции, проходящее через нач корд.

3)Определить направление роста (убывания) целевой функции, перемещая прямую (пл-ть), соотв-щую целевой ф-ции, параллельно самой себе.

4)В соответствии с целью ЗЛП и направлением роста (убывания) целевой функции найти точку касания этой прямой (пл-ти) с многоугольником (многогр) ограничений – вершину многоуг-ка, имеющую мах отклонение от прямой (пл-ти), проходящей через начало корд.

Графическая интерпретация случая неограниченной целевой функции.

По определению множество называется неограниченным , если нельзя построить сферы конечного радиуса из какой либо точки множества , включающую все это множество. Графики неиграниченное множество представляющее собой незамкнутый многоугольник. Также для если рассмотреть подробнее , для того , чтобы показать , что для неограниченности множества решений достаточно наличие возможности бесконечного роста хотябы одной независимой переменной.

Случай несовместимости возникает тогда, когда общей области пересекающихся полуплоскостей или оно попадает в отриц. В этом случае гворят, что множество решений пустое.

1. Анализ чувствительности линейных моделей к изменению значений параметров системы ограничений (постановка задачи).
2. Анализ чувствительности линейных моделей к изменению значений параметров функции цели (постановка задачи)
3. Транспортная задача ЛП

ТЗЛП заключается в определении объема перевозок от поставщиков к потребителям, если известны выпуск продукции у каждого поставщика и потребности потребителей; затраты на перемещение грузов от поставщиков к потребителям. План грузоперевозок для им.min затраты. Причем это могут быть затраты денежных средств, транспортных работ или перевозок.

Особенности транспортной задачи

1) Все ограничения имеют вид равенств

2) Каждая переменная входит всего 2 ограничения.

3) Коэффициент при переменных в ограничениях =1

Решение задач ТЗЛП включает 2 основных этапа построение опорного решения (начального плана перевозок) и построение оптимального решения.

Построение опорного решения. Оно может быть получено методами северо-западного угла, наименьших стоимостей и двойного предпочтения. Наиболее простым и легко формализуемым является метод северо-западного угла, однако он даёт обычно решение, далёкое от оптимального. При построении опорного решения методами наименьших стоимостей и двойного предпочтения анализируется матрица затрат и начальный план обычно близок к оптимальному. Метод с-з угла используется, как правило, при расчётах на ПК. При его применении данные о стоимостях не нужны.

Условия и метод построения оптимального решения транспортной задачи.

Один из наиболее простых и распространённых методов оптимизации транспортной задачи – метод потенциалов. Условия оптимальности плана транспортной задачи существует тогда, когда им соответствуют условия потенциальности оптимального плана транспортной задачи.

Условие потенциальности показывает, что разность потенциалов потребителя и поставщика = стоимости перевозки между ними, если перевозка осуществляется, и не больше стоимости перевозки при её отсутствии.

Алгоритм решения транспортной задачи методом потенциалов состоит из двух этапов: предварительного и общего. Первый включает: 1. построение опорного решения 2. присвоение и расчёт системы потенциалов 3. проверка первоначального плана на оптимальность. Если опорное решение не является оптимальным, то переходят ко второму (общему) этапу, который включает: 1. улучшение плана перевозок 2. исправление системы потенциалов 3. проверка улучшенного плана на оптимальность. Общий шаг циклически выполняется до получения оптимального плана перевозок.

Алгоритм решения транспортной задачи на сети. В ряде случаев транспортную задачу целесообразно решать в сетевой постановке, отличающейся наглядностью. Транспортная сеть это совокупность вершин или узлов (пункты отправления и приёма грузов, промежуточные пункты) и соединяющих их транспортных коммуникаций или звеньев. На каждом звене проставляются удельная стоимость перевозки груза по данному транспортному участку Сij , а при ограниченности пропускной способности звена также и её максимальное значение dij. Около каждой вершины в скобках со знаком + или – проставляются объемы отправления и приёма грузов. Соответственно.

Нахождение оптимального при сетевой постановке транспортной задачи плана осуществляется методом потенциалов: 1)Строится опорное решение 2) Для построения системы потенциалов любой вершине присваивается какой-л потенциал. 3)Проверка плана на оптимальность осуществляется для всех звеньев без грузопотока. 4) При улучшении плана по звену, на котором нарушено первое условие оптимальности (разность потенциалов потребителя и поставки = стоимости перевозки между ними), должна пройти перевозка; если нарушено 3е условие опт-ти (разность потенциалов потребителя и поставка должна быть больше стоимости перевозок по звену если по нему осуществляется перевозка, объёмом равной его пропускной способности), то на этом звене перевозка должна уменьшаться.

Постановка и решение ТЗ по критерию времени.

Иногда (перевозка возгорающихся полезных ископаемых, оперативное управление работой транспорта и др.) перевозку грузов от поставщиков i=1,n до потребителей j=1,m необходимо спланировать и организовать за минимальное время.

Решение ТЗ задачи по критерию времени осуществляется в следующем порядке. 1) Методом с-з угла или наименьшего элемента троится опорное решение ТЗ. 2)Из всех клеток, занятых перевозками, выбирается наибольшее время. 3) Клетки исходной матрицы, в которых время перевозки превышает максимальное для допустимого плана, зачёркиваются. 4)Улучшается допустимый план 5) Улучшение допустимого плана осуществляется до тех пор, пока полученный план не станет оптимальным

Источник